Δυναμική στο Επίπεδο: Δράση-Αντίδραση, Σύνθεση-Ανάλυση Δυνάμεων

Α΄ Λυκείου, Λύκειο
Comments

Το Διάγραμμα Ελεύθερου Σώματος (ΔΕΣ)

Πριν ο μαθητής προχωρήσει στη λύση ασκήσεων και στην απάντηση ερωτήσεων, είναι χρήσιμο να κατανοήσει τι είναι, πώς κατασκευάζεται και πώς βοηθάει το Διάγραμμα Ελεύθερου Σώματος στη διαδικασία της λύσης.

Το ΔΕΣ είναι ένα διάγραμμα που δείχνει τα σχετικά μέτρα και τις κατευθύνσεις όλων των δυνάμεων που ασκούνται πάνω σε ένα σώμα, σε μια δεδομένη κατάσταση.

Οι δυνάμεις απεικονίζονται με διανύσματα (βέλη). Τα μήκη των διανυσμάτων πρέπει να αντιστοιχούν στα μέτρα των δυνάμεων και οι κατευθύνσεις τους δείχνουν τις κατευθύνσεις των δυνάμεων.

Τα σώματα συνήθως τα σχεδιάζουμε ως μικρά παραλληλόγραμμα, με τις  δυνάμεις να ασκούνται στο κέντρο τους ή σημεία, με τις δυνάμεις να ασκούνται στο σημείο που εκφράζει το σώμα. Ας μη ξεχνάμε ότι οι διαστάσεις των σωμάτων, σ’ αυτή τη φάση, δε μας ενδιαφέρουν και όλα τα σώματα τα θεωρούμε ως υλικά σημεία.

Όταν κατασκευάζουμε για ένα σώμα το ΔΕΣ, σχεδιάζουμε μόνο το σώμα αυτό με τις δυνάμεις που ασκούνται επάνω του και κανένα άλλο, έστω κι αν το σώμα βρίσκεται σε απαφή με άλλα. Π.χ. ας υποθέσουμε ότι έχουμε πάνω σε μία οριζόντια επιφάνεια ακίνητο ένα αντικείμενο Σ [Εικ. 1(α)]. Στην Εικ. 1 (β) και Εικ. 1 (γ) είναι τα διαγράμματα ελεύθερου σώματος του αντικειμένου Σ και της επιφάνειας αντίστοιχα.

Εικ. 1: (α) είναι το αώμα Σ ακίνητο πάνω σε μία οριζόντια επιφάνεια. (β) ΔΕΣ του σώματος Σ. Το Σ έχει σχεδιαστεί ως μικρό τετράγωνο και επάνω του ασκούνται το βάρος του W και η κάθετη δύναμη Ν της επιφάνειας. (γ) ΔΕΣ της επιφάνειας. Στην επιφάνεια ασκείται η δύναμη Ν, με βάση το νόμο Δράσης-Αντίδρασης του Νεύτωνα. Οι δύο δυνάμεις W kai N σχεδιάστηκαν με ίσα μήκη.

Εικ. 1: (α) Το σώμα Σ ακίνητο πάνω σε μία οριζόντια επιφάνεια. (β) ΔΕΣ του Σ. Το Σ έχει σχεδιαστεί ως μικρό παραλληλόγραμμο και επάνω του ασκούνται το βάρος του W και η κάθετη δύναμη Ν της επιφάνειας. (γ) ΔΕΣ της επιφάνειας. Στην επιφάνεια ασκείται η δύναμη Ν, με βάση το νόμο Δράσης-Αντίδρασης του Νεύτωνα. Οι δύο δυνάμεις W και N σχεδιάστηκαν με ίσα μήκη.

Δες και το άρθρο του Albert Lee “Πώς σχεδιάζουμε ένα σωστό Διάγραμμα Ελευθέρου Σώματος”

Στις ασκήσεις που ακολουθούν όλα τα σχοινιά και νήματα θεωρούνται αβαρή. Αβαρείς και χωρίς διαστάσεις θεωρούνται και οι τροχαλίες. Επίσης, όπου δεν αναφέρεται ρητά ότι οι επιφάνειες είναι λείες, να λαμβάνονται υπόψη οι τριβές.

  1. Το μπαλάκι του τένις κτυπάει στη ρακέτα και επιστρέφει με αντίθετη κατεύθυνση.
    1. Σχεδίασε το διάγραμμα ελεύθερου σώματος για το μπαλάκι και τη ρακέτα.
    2. Το μπαλάκι, που έχει μάζα 58,5gr, πέφτει πάνω στη ρακέτα με ταχύτητα 40m/s και επιστρέφει με -60m/s. Να συγκρίνεις τις δυνάμεις που αλληλεπιδρούν το μπαλάκι και η ρακέτα, στον μικρό χρόνο του 1ms που είναι σε επαφή μεταξύ τους. Με πόση δύναμη κτυπάει τη ρακέτα το μπαλάκι;

    Άσκηση 1

    Άσκηση 1

  2. Κρατάμε τη σφαίρα Σ ακίνητη μέσω ενός κατακόρυφου νήματος. Σχεδίασε τα διαγράμματα ελεύθερου σώματος για το Σ, το νήμα και το χέρι.
    Άσκηση 1

    Άσκηση 2

    (περισσότερα…)

Δυναμική σε μία Διάσταση Online: Πολλαπλής Επιλογής

Online, Α΄ Λυκείου, Λύκειο
Comments

Δοκίμασε να απαντήσεις στις 20 ερωτήσεις πολλαπλής επιλογής και αντιστοίχισης που βαθμολογούνται από 1 μονάδα η κάθε μία.

Όταν ολοκληρώσεις τις απαντήσεις πάτα το "Αποτελέσματα" και αυτόματα θα δεις τις σωστές απαντήσεις και την επίδοσή σου.

Σε όλες τις ερωτήσεις η τιμή της επιτάχυνσης της βαρύτητας είναι g=9,8m/s2.

1. Για να μετατρέψουμε ένα ελατήριο σε δυναμόμετρο:
2. Σύμφωνα με τον πρώτο νόμο του Νεύτωνα:
3. Σύμφωνα με το δεύτερο νόμο του Νεύτωνα, \vec{F}=m \cdot \vec{a} :
4. Σε ένα αντικείμενο ασκείται συνισταμένη δύναμη 20Ν και το επιταχύνει με 4m/s2. Για να επιταχυνθεί με 1m/s2 η συνισταμένη δύναμη θα πρέπει να είναι:
5. Μία δύναμη δίνει επιτάχυνση 3m/s2 σε ένα σώμα μάζας 12kg. Η ίδια δύναμη, αν ασκηθεί σε σώμα μάζας 2kg θα δώσει επιτάχυνση:
6. Οριζόντια συνισταμένη δυναμη 1Ν ασκείται σε σώμα βάρους 1Ν που μπορεί να κινηθεί ελεύθερα χωρίς τριβές σε οριζόντιο επίεπδο. Η επιτάχυνση που αποκτά το σώμα είναι:
7. Στο σώμα μάζας 20kg ασκούνται οι τρεις δυνάμεις F1, F2 και F3 με μέτρα 60Ν, 40Ν και 20Ν αντίστοιχα. Το σώμα κινείται προς τα δεξιά χωρίς τριβή. Ποιες από τις παρακάτω προτάσεις είναι σωστές;

Ερώτηση 6

Ερώτηση 7

8. Σώμα Α, με μάζα 5kg και σώμα Β με βάρος 50N βρίσκονται ακίνητα στο δάπεδο. Ασκούμε στα σώματα από μία δύναμη 50N κατακόρυφα προς τα πάνω. Επέλεξε τη σωστή πρόταση.
9. Αντιστοίχισε τις περιπτώσεις της μεταβολής μάζας και συνισταμένης δύναμης στην αριστερή στήλη με τα αποτελέσματα στην επιτάχυνση του σώματος στη δεξιά. (Επέλεξε με κλικ δεξιά).
Η μάζα και η συνισταμένη αυξάνονται 3 φορές.
Η επιτάχυνση αυξάνεται 9 φορές.

Unselect

Η επιτάχυνση μειώνεται 9 φορές.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η επιτάχυνση μηδενίζεται.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η μάζα και η συνισταμένη μειώνονται 3 φορές.
Η επιτάχυνση αυξάνεται 9 φορές.

Unselect

Η επιτάχυνση μειώνεται 9 φορές.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η επιτάχυνση μηδενίζεται.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η μάζα αυξάνεται 3 φορές και η συνισταμένη μειώνεται 3 φορές.
Η επιτάχυνση αυξάνεται 9 φορές.

Unselect

Η επιτάχυνση μειώνεται 9 φορές.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η επιτάχυνση μηδενίζεται.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η μάζα μειώνεται 3 φορές και η συνισταμένη αυξάνεται 3 φορές.
Η επιτάχυνση αυξάνεται 9 φορές.

Unselect

Η επιτάχυνση μειώνεται 9 φορές.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η επιτάχυνση μηδενίζεται.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η μάζα μειώνεται 3 φορές και η συνισταμένη γίνεται μηδέν.
Η επιτάχυνση αυξάνεται 9 φορές.

Unselect

Η επιτάχυνση μειώνεται 9 φορές.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

Η επιτάχυνση μηδενίζεται.

Unselect

Η επιτάχυνση παραμένει σταθερή.

Unselect

10. Δύο σώματα Α και Β κινούνται χωρίς τριβές σε οριζόντιο επίπεδο με ίσες ταχύτητες. Ασκούμε ίσες οριζόντιες δυνάμεις στα δύο σώματα και τα σταματάμε. Αν το Β κάνει περισσότερο χρόνο για να σταματήσει, τότε:
11. Η σφαίρα είναι δεμένη με νήμα και ανεβαίνει προς τα πάνω με σταθερή ταχύτητα, χωρίς αντιστάσεις. Κάποια στιγμή το νήμα κόβεται. Τότε το σώμα:

Ερώτηση 11

Ερώτηση 11

12. Διαθέτουμε τέσσερα σώματα Α,Β,Γ και Δ, που βρίσκονται σε ηρεμία και μπορούν να κινηθούν χωρίς τριβές πάνω σε οριζόντιο επίπεδο. Στα σώματα ασκούμε τις οριζόντιες δυνάμεις FA, FΒ, FΓ και FΔ αντίστοιχα και τα θέτουμε σε κίνηση. Κατάταξε τις δυναμεις (σύρε με το ποντίκι) που ασκούνται στα τέσσερα σώματα από τη μεγαλύτερη προς τη μικρότερη, λαμβάνοντας υπόψη τα παρακάτω δεδομένα. (Δύσκολη)
  1. Τα Α και Β αποκτούν την ίδια επιτάχυνση, αλλά το Α έχει τη μισή μάζα του Β.
  2. Τα Γ και Δ έχουν την ίδια μάζα, αλλά το Γ αποκτά διπλάσια επιτάχυνση από το Δ.
  3. Το Α αποκτά τριπλάσια επιτάχυνση από το Δ, αλλά η μάζα το Δ έχει τετραπάσια μάζα.
  4. Το Β αποκτά την ίδια επιτάχυνση με Γ, αλλά τριπλάσια επιτάχυνση από το Δ.
  • FΑ
  • FΓ
  • FΒ
  • FΔ
13. Ένα όχημα φρενάρει και η ταχύτητά του μεταβάλλεται από 30m/s σε 10m/s σε χρόνο 4s. Αν η δύναμη που ασκεί ο δρόμος για να το φρενάρει είναι  6000Ν, η μάζα του οχήματος θα είναι:
14. Η εξίσωση της ταχύτητας ενός σώματος μάζας 20kg, που κινείται ευθύγραμμα, είναι v=40m/s-(16m/s^2) \cdot t .  Στο σώμα ασκείται συνισταμένη δύναμη:
15. Το διάγραμμα δείχνει τη συνισταμένη δύναμη που ασκείται σε σώμα μάζας 5kg, καθώς μεταβάλλεται με το χρόνο. Επέλεξε τις σωστές προτάσεις, λαμβάνοντας υπόψη ότι το σώμα αρχικά βρισκόταν σε ηρεμία.

Ερώτηση 15

Ερώτηση 15

16. Το διάγραμμα περιγάφει την εξέλιξη της ταχύτητας ενός σώματος, που κινείται σε οριζόντιο επίπεδο ευθύγραμμα χωρίς τριβές, σε συνάρτηση με το χρόνο. Επέλεξε ποιες από τις παρακάτω προτάσεις χαρακτηρίζουν σωστά τη συνισταμένη των δυνάμεων που ασκούνται στο σώμα.

Ερώτηση 16

Ερώτηση 16

17. Ένα σώμα ξεκινά από την ηρεμία υπό την επίδραση οριζόντιας δύναμης και κινείται χωρίς τριβές σε οριζόντιο επίπεδο. Το διάγραμμα δείχνει τη θέση του σώματος σε συνάρτηση με το χρόνο. Ποιες από τις προτάσεις είναι σωστές;

Πολλαπλής 6

Ερώτηση 17

18. Δύο σώματα Α και Β αφήνονται ταυτόχρονα να πέσουν ελεύθερα από διαφορετικά ύψη. Το σώμα Β πέφτει από διπλάσιο ύψος από το Α. Αν ο χρόνος που χρειάζεται το Α για να φτάσει στο έδαφος είναι t, τότε ο χρόνος του Β είναι:
19. Ένας άνθρωπος βλέπει από το παράθυρό του να πέφτει μία γλάστρα. Η γλάστρα κάνει 0,115s για να διανύσει το μήκος του παράθυρου και να χαθεί από την ορατότητα του ανθρώπου. Αν το μήκος του παράθυρου είναι 1,2m, επέλεξε πόσο χρόνο, πριν εμφανιστεί η γλάστρα στο πάνω μέρος του, άρχισε την ελεύθερη πτώση της.
20. Η εξίσωση που περιγράφει την ελεύθερη πτώση ενός σώματος είναι h=44,1m-(4,9m/s^2) \cdot t^2. Όπου h είναι το ύψος από το έδαφος και t ο χρόνος. Ποιες από τις παρακάτω προτάσεις είναι σωστές;

 


Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

img_1494

Δυναμική σε μία Διάσταση Online: Σωστό-Λάθος

Online, Α΄ Λυκείου, Λύκειο
Comments

Please go to Δυναμική σε μία Διάσταση Online: Σωστό-Λάθος to view this quiz
Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

img_1494

Δυναμική σε μία διάσταση – Ασκήσεις

Α΄ Λυκείου, Λύκειο
Comments
  1. Το ελατήριο στη θέση Κ βρίσκεται στο φυσικό του μήκος. Με την επίδραση κατάλληλης δύναμης μπορούμε να δημιουργήσουμε συσπείρωση (θέση Λ) ή επιμήκυνση (θέση Μ) κατά Δl. Πώς πρέπει να ασκηθεί η δύναμη στην άκρη του ελατηρίου στις δύο θέσεις Λ και Μ; Σε τι διαφέρουν μεταξύ τους;

    Άσκηση 1

    Άσκηση 1

  2. Όταν κρεμάσουμε σε ένα ελατήριο ένα δίλιτρο (2lt) δοχείο λαδιού προκαλείται επιμήκυνση 12cm. Πόσο θα είναι το βάρος μιας συσκευασίας ζάχαρης που προκαλεί επιμήκυνση στο ίδιο ελατήριο 18cm; Δίνεται η πυκνότητα το λαδιού ρ=0,8gr/ml.
  3. Σε ένα πολύ μικρό σώμα ασκούνται οι πέντε οριζόντιες δυνάμεις που φαίνονται στην εικόνα. Υπολογίστε τη δύναμη που μπορεί να αντικαταστήσει και τις πέντε και σχεδιάστε την. Δίνονται τα μέτρα πέντε δυνάμεων: F1=80N, F2=50N, F3=60N, F4=70N, F5=100N

    Άσκηση 2

    Άσκηση 3

  4.  Το μικρό σώμα κινείται προς τα αριστερά και ασκούνται επάνω του μόνο οι τρεις δυνάμεις της εικόνας. Τα μέτρα των δυνάμεων είναι F1=90N, F2=60N και F3=30N. Η κίνηση που εκτελεί το σώμα είναι:
    1. Ευθύγραμμη ομαλή
    2. Ευθύγραμμη ομαλά επιταχυνόμενη
    3. Ευθύγραμμη ομαλά επιβραδυνόμενη

    Επέλεξε τη σωστή πρόταση και δικαιολόγησε την απάντησή σου.

    Άσκηση 3

    Άσκηση 4

  5. Υπόθεσε ότι είσαι συνεπιβάτης σε ένα αυτοκίνητο που τρέχει μόνο με 40km/h και ξέχασες να φορέσεις τη ζώνη ασφαλείας. Ξαφνικά στη μέση του δρόμου πετάγεται ένας σκύλος και ο οδηγός φρενάρει απότομα για να μην τον κτυπήσει. Με πόση ταχύτητα και γιατί θα κτυπήσεις στο ταμπλώ του αυτοκινήτου; Σύγκρινε την ταχύτητα αυτή με την ταχύτητα του Γιουσέιν Μπόλτ, όταν κατέρριπτε το παγκόσμιο ρεκόρ στους Ολυμπιακούς του Πεκίνου το 2008 με 9,58s. (Ο οδηγός τελικά δεν κτυπάει τον σκύλο).
  6. Το κοντέρ ενός αυτοκινήτου δείχνει σταθερά 60km/h για αρκετό χρονικό διάστημα. Παρόλα αυτά η μηχανή του αυτοκινήτου λειτουργεί και ο οδηγός πατάει το γκάζι. Γιατί τότε το αυτοκίνητο δεν επιταχύνεται, αλλά έχει σταθερή ταχύτητα;
  7. Οι οριζόντιες δυνάμεις της εικόνας έχουν μέτρα F1=20N και F2=10N και το σώμα κινείται προς τα δεξιά. Στις τρεις περιπτώσεις Α, Β και Γ σχεδίασε τα διανύσματα των επιταχύνσεων και βρείτε τι είδους κίνηση εκτελεί το σώμα.

    Άσκηση 7

    Άσκηση 7

  8. Πόση δυναμη πρέπει να ασκείται σε άνα σώμα μάζας 5kg, ώστε σε χρόνο 3s να αυξήσει την ταχύτητά του κατά 15m/s;
  9. Σώμα μάζας 3kg ξεκινάει από την ηρεμία και κινείται σε λείο οριζόντιο επίπεδο με την επίδραση οριζόντιας δύναμης. Υπολόγισε τη δύναμη που ασκείται στο σώμα στις περιπτώσεις που:
    1. Σε 10s διανύει 150m.
    2. Σε 4s αποκτάει ταχύτητα 16m/s.
  10. Σωματίδιο μάζας 10-5gr επιταχύνεται ξεκινώντας από την ηρεμία, υπό την επίδραση σταθερής δύναμης ηλεκτρικού πεδίου μέτρου F=0,3N. Μετά από 1ms:
    1. Πόση ταχύτητα θα έχει αποκτήσει;
    2. Πόσο διάστημα θα έχει διανύσει;

    Το βαρυτικό πεδίο θεωρείται αμελητέο. (περισσότερα…)

Η Ειδική Θεωρία της Σχετικότητας

Επιστήμη
Comments

Του Richard P. Feynman

Ο Richard P. Feynman, ήταν ένας από τους σημαντικότερους θεωρητικούς φυσικούς του 20ου αιώνα και τιμήθηκε με το βραβείο Νόμπελ το 1965 για τη συμβολή του στην Κβαντική Ηλεκτροδυναμική, Οι διαλέξεις του έμειναν στην ιστορία της επιστήμης ως άριστο παράδειγμα εκλαΐκευσης σπουδαίων φυσικών εννοιών, με αποκορύφωμα την επινόηση των “διαγραμμάτων Φάινμαν”, με τα οποία απλοποιήθηκαν οι υπολογισμοί για την αλληλεπίδραση των στοιχειωδών σωματιδίων.

Μία από τις διάσημες διαλέξεις του Φάινμαν ήταν η διάλεξή του για την Ειδική Θεωρία της Σχετικότητας, η οποία δημοσιεύτηκε το 1964, ένα χρόνο δηλαδή πριν του απενεμηθεί το Βραβείο Νόμπελ, στο αμερικάνικο περιοδικό The Physics Teacher.

Είναι μία ευκαιρία για τους φυσικούς να φρεσκάρουν τις γνώσεις τους, αλλά και κάθε ένας που διαθέτει ικανοποιητικό μαθηματικό μπακράουντ και ενδιαφέρον για τις φυσικές επιστήμες να έρθει σε απαφή με μία από τις μεγαλύτερες επιστημονικές θεωρίες.

 

Η Αρχή της Σχετικότητας

Για περισσότερα από 200 χρόνια πίστευαν ότι οι εξισώσεις της κίνησης που διατυπώθηκαν από τον Νεύτωνα περιέγραφαν σωστά τη φύση, και  όταν ανακαλύφθηκε το πρώτο σφάλμα σε αυτούς τους νόμους, είχε ήδη ανακαλυφθεί και ο τρόπος για να διορθωθεί. Τόσο το λάθος όσο και η διόρθωσή του ανακαλύφθηκαν από τον Άινστάιν το 1905.
Ο Δεύτερος νόμος του Νεύτωνα, το οποίο έχουμε εκφράσει με την εξίσωση

    \[ F=\frac{d(mv)}{dt} \]

διατυπώθηκε με την σιωπηρή παραδοχή ότι η μάζα m είναι σταθερή, αλλά τώρα ξέρουμε ότι αυτό δεν είναι αλήθεια και ότι η μάζα ενός σώματος αυξάνεται με την ταχύτητα. Στο διορθωμένο τύπο του Αϊνστάιν το m παίρνει την τιμή

 

(1)   \begin{equation*} m=\frac{m_0}{\sqrt{1-v^2/c^2}} \end{equation*}

 

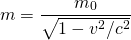
όπου η “μάζα ηρεμίας” m0 αντιπροσωπεύει τη μάζα ενός σώματος, όταν αυτό δεν κινείται και c η ταχύτητα του φωτός, η οποία είναι περίπου 3×105 km/s.
Για εκείνους που θέλουν να μάθουν απλώς όσα χρειάζονται για να μπορούν να λύνουν προβλήματα, αυτό είναι αρκετό για τη θεωρία της σχετικότητας. Αλλάζουν απλώς τους νόμους του Νεύτωνα εισάγοντας έναν παράγοντα διόρθωσης στη μάζα. Από τον ίδιο τον τύπο, είναι εύκολο να δούμε ότι αυτή η αύξηση της μάζας είναι πολύ μικρή σε κανονικές συνθήκες. Ακόμη κι αν η ταχύτητα είναι τόσο μεγάλη όσο ενός δορυφόρου, που περιστρέφεται γύρω από τη Γη με 8km/ sec, τότε υ/c = 8 / 300.000. Αντικαθιστώντας στον τύπο γίνεται φανερό ότι η διόρθωση στη μάζα είναι της τάξεως μόνο του ενός προς δύο με τρία δισεκατομμυριοστά, η οποία είναι αδύνατον να παρατηρηθεί. Στην πραγματικότητα, η ορθότητα του τύπου έχει επιβεβαιωθεί πλήρως από την παρατήρηση πολλών ειδών σωματιδίων, που κινούνται με ταχύτητες που φθάνουν σχεδόν την ταχύτητα του φωτός. Ωστόσο, επειδή το αποτέλεσμα είναι συνήθως πολύ μικρό, είναι αξιοσημείωτο το γεγονός ότι ανακαλύφθηκε θεωρητικά πριν ανακαλυφθεί πειραματικά. Εμπειρικά, σε αρκούντως υψηλή ταχύτητα, το αποτέλεσμα είναι πολύ μεγάλο, αλλά δεν ανακαλύφθηκε μ’ αυτόν τον τρόπο. Ως εκ τούτου, είναι ενδιαφέρον να δούμε πώς ένας νόμος όπου εμπλέκονται τόσο λεπτές τροποποιήσεις (κατά τη στιγμή που ανακαλύφθηκε για πρώτη φορά) ήλθε στο φως από έναν συνδυασμό πειραμάτων και εύλογων συλλογισμών. Συνεισφορές στην ανακάλυψη έγιναν από έναν αριθμό ανθρώπων, το τελικό αποτέλεσμα των εργασιών των οποίων ήταν η ανακάλυψη του Αϊνστάιν.

Υπάρχουν πραγματικά δύο θεωρίες της σχετικότητας του Αϊνστάιν. Αυτό το κεφάλαιο ασχολείται με την Ειδική Θεωρία της Σχετικότητας, η οποία χρονολογείται από το 1905. Το 1915 ο Αϊνστάιν δημοσίευσε μια πρόσθετη θεωρία, που ονομάζεται Γενική Θεωρία της Σχετικότητας. Η τελευταία αυτή πραγματεύεται μία θεωρία με την επέκταση της Ειδικής Θεωρίας στην περίπτωση του νόμου της βαρύτητας. Δεν θα συζητήσουμε τη Γενική Θεωρία εδώ.

Η αρχή της σχετικότητας αναφέρθηκε για πρώτη φορά από το Νεύτωνα, σε ένα από τα πορίσματά του στους νόμους της κίνησης: “Οι κινήσεις των σωμάτων που περιλαμβάνονται σε ένα συγκεκριμένο χώρο είναι ίδιες μεταξύ τους, είτε ο χώρος είναι σε κατάσταση ηρεμίας ή κινείται προς τα εμπρός ευθύγραμμα και ομαλά.” Αυτό σημαίνει, για παράδειγμα, ότι αν ένα διαστημόπλοιο κινείται ευθύγραμμα και ομαλά, όλα τα πειράματα που εκτελούνται στο διαστημόπλοιο και όλα τα φαινόμενα που συμβαίνουν στο διαστημόπλοιο, θα εμφανίζονται τα ίδια όπως εάν το διαστημόπλοιο δεν κινείται, υπό την προϋπόθεση, φυσικά, ότι δεν βλέπεις προς τα έξω. Αυτό είναι το νόημα της αρχής της σχετικότητας. Είναι μια αρκετά απλή ιδέα και το μόνο ερώτημα που τίθεται είναι, αν είναι αλήθεια, ότι όλα τα πειράματα που εκτελούνται μέσα σε ένα κινούμενο σύστημα και οι νόμοι της φυσικής, είναι ίδιοι, όπως θα ήταν, αν το σύστημα ήταν ακίνητο. Ας εξετάσουμε πρώτα κατά πόσον οι νόμοι του Νεύτωνα παραμένουν οι ίδιοι σε κινούμενο σύστημα.

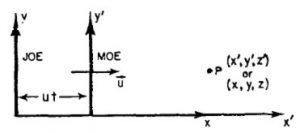
Σχετικότητα 1

Εικ. 1. Δύο συστήματα αναφοράς που κινούνται με σταθερή σχετική μεταξύ τους ταχύτητα κατά μήκος του άξονα x.


Ας υποθέσουμε ότι ο Moe κινείται προς τη διεύθυνση x με σταθερή ταχύτητα u και μετρά τη θέση ενός σταθερού σημείου Ρ, που φαίνεται στην Εικ. 1. Η  “x-απόσταση” του Moe από το σημείο P στο σύστημα συντεταγμένων του παριστάνεται με x΄.  Ο Joe είναι σε κατάσταση ηρεμίας και μετρά την θέση του ίδιου σημείου, στο δικό του σύστημα ως x. Η σχέση των συντεταγμένων στα δύο συστήματα είναι σαφής από το διάγραμμα. Μετά από χρόνο t η αρχική θέση του Moe έχει μετακινηθεί απόσταση ut, και εάν τα δύο συστήματα αρχικά συνέπιπταν θα έχουμε:
 (περισσότερα…)

Η φύση του Ηλεκτρονίου

Επιστήμη
2 Comments

Η αναζήτηση της φύσης του ηλεκτρονίου και της φύσης του φωτός αποτέλεσαν δύο από τα μεγαλύτερα προβλήματα της Φυσικής και λαμπρό πεδίο ερευνών όλων των μεγάλων επιστημόνων.  Ο καθηγητής-ερευνητής Don Licoln του Fermilab στο Σικάγο, ΗΠΑ, μας έχει δώσει πολλά άρθρα με τα οποία εκλαϊκεύει σύνθετες έννοιες της φυσικής, έτσι ώστε να δίνει την ευκαιρία σε όλους όσους διαθέτουν ένα σχετικά ανεκτό επίπεδο γνώσεων, να μπορούν να αντιλαμβάνονται τους βαθύτερους μηχανισμούς που διέπουν τα φυσικά φαινόμενα.

Στο παρακάτω άρθρο αναλύει σε σημαντικό βάθος τη φύση του ηλεκτρονίου, για το οποίο εκείνο που όλοι γνωρίζουμε είναι ότι πρόκειται για ένα μικρότατο σωματίδιο, συστατικό του κάθε ατόμου, έχει αρνητικό φορτίο και περιστρέφεται γύρω από τον πυρήνα. Πόσο κοντά στην πραγματικότητα είμαστε; Μήπως μπροστά μας έχουμε ένα πολύ πιο σύνθετο αντικείμενο, για το οποίο πολλά γνωρίζουμε, αλλά ακόμη πιο πολλά έχουμε να μάθουμε;

  • Του Don Licoln, καθηγητή-ερευνητή στο Fermilab, Chicago
  • Από το The Physics Teacher Magazine

Ο Winston Churchill είπε κάποτε ότι η Ρωσία ήταν ένα αίνιγμα τυλιγμένο στο μυστήριο μέσα σε ένα αίνιγμα. Αν το “Εγγλέζικο Μπουλντόγκ” ήταν φυσικός, θα μπορούσε να μιλήσει για κάτι άλλο, εκτός από τους Σλάβους συντρόφους μας. Θα μπορούσε να μιλήσει για το ηλεκτρόνιο.

Μπορεί να φαίνεται περίεργο να σκεφτούμε το ηλεκτρόνιο ως ένα μυστηριώδες σωματίδιο. Εξ άλλου, εκπαιδευτικοί που διδάσκουν εισαγωγική φυσική, διδάσκουν παντού τους μαθητές για το φορτίο και το ρεύμα και  κάνουν εργαστήρια για τον υπολογισμό του λόγου φορτίου προς μάζα του σωματιδίου. Αν είναι αρκετά εύκολο να καταλάβουμε ότι μπορούμε να παρουσιάσουμε τις τεχνικές λεπτομέρειες του σωματιδίου στους πρωτοετείς φοιτητές της φυσικής, τότε πόσο μυστηριώδες μπορεί να είναι;

Βέβαια, πιθανώς τώρα να γύρισαν οι σκέψεις σας στην κβαντική των ηλεκτρονίων και την εξίσωση του Schrödinger και στο αν οι γάτες είναι ζωντανές ή νεκρές, και ίσως αρχίσετε να θυμόσαστε ότι το ηλεκτρόνιο δεν μας έχει πει όλες τις ιστορίες του. Και η ιστορία της κβαντικής μηχανικής είναι πλέον παλιά, σχεδόν έναν αιώνα. Η επιστήμη έχει προχωρήσει και οι ερευνητές έχουν εγκαταλείψει τις απλούστερες κβαντικές παραστάσεις του ηλεκτρονίου για τις πιο προηγμένες της σχετικιστικής κβαντομηχανικής και της θεωρίας των κβαντικών πεδίων. Όπως η Σαλώμη, στην όπερα του Ρίχαρντ Στράους, το ηλεκτρόνιο φαίνεται να κάνει το χορό των επτά πέπλων και ο χορός δεν έχει ακόμη τελειώσει. Το ηλεκτρόνιο έχει ακόμα μερικά μυστικά να αποκαλύψει.

Αυτό το άρθρο θα καλύψει κυρίως τις πιο σύγχρονες αναπαραστάσεις του ηλεκτρονίου. Η ιστορία θα ξεκινήσει με μια σύντομη υπενθύμιση των ηλεκτρονίων της κλασικής φυσικής και των αρχών της κβαντικής θεωριάς, αλλά αυτά θα χρησιμοποιηθούν μόνο ως εφααλτήρια για να βυθιστούμε στην ιστορία των σύγχρονων ηλεκτρονίων. Και, όπως θα δούμε, αυτή η ιστορία πηγαίνει πολύ βαθιά.

 

Το αρχικό ηλεκτρόνιο

 

Μία συσκευή σαν το σωλήνα του Crookes, που εικονίζερται εδώ, επέτρεψε στους φυσικούς του 19ου αιώνα να μελετήσουν τις καθοδικές ακτίνες, ως μία πρώτη προσπάθεια να αντιληφυούν αυτό σήμερα αποκαλούμε ηλεκτρόνιο.

Εικ. 1. Μία συσκευή σαν το σωλήνα του Crookes, που εικονίζεται εδώ, επέτρεψε στους φυσικούς του 19ου αιώνα να μελετήσουν τις καθοδικές ακτίνες, ως μία πρώτη προσπάθεια να αντιληφθούν αυτό που σήμερα αποκαλούμε ηλεκτρόνιο.

(περισσότερα…)

Νόμοι της Υδροστατικής Πίεσης – Εργαστήριο

Β΄ Γυμνασίου, Γυμνάσιο
4 Comments

Εκτελέστε τα βήματα που ακολουθούν για να ανακαλύψετε τους Νόμους της Υδροστατικής Πίεσης.

Υδροστατική πίεση ονομάζουμε την πίεση στο εσωτερικό των υγρών που ισορροπούν.

Θα βρείτε πώς εξαρτάται η υδροστατική πίεση από:

  • Το βάθος
  • Την πυκνότητα του υγρού
  • Την επιτάχυνση της βαρύτητας

Το Βάθος

Βήμα 1

Στο πινακάκι δεξιά πάνω απενεργοποιήστε την ατμοσφαιρική πίεση (κλικ στο Off) και ενεργοποιήστε το Ruler και το Grid (κλικ στα κυκλάκια). Με διαδοχικά κλικ στην κάνουλα της πάνω βρύσης γεμίστε με νερό τη δεξαμενή. Ευθυγραμμίστε το 0 του μέτρου με την επιφάνεια του νερού.
(περισσότερα…)

Η ανίχνευση των Βαρυτικών Κυμάτων

Επιστήμη
1 Comment

Στις 11 φεβρουαρίου 2016 το Παρατηρητήριο Βαρυτικών Κυμάτων LIGO, WA, ανακοίνωσε:

“Ανοίγει το νέο παράθυρο στο Σύμπαν με την παρατήρηση των βαρυτικών κυμάτων από συγκρουόμενες μαύρες οπές.
Για πρώτη φορά, οι επιστήμονες έχουν παρατηρήσει κυματισμούς στον ιστό του χωροχρόνου που ονομάζονται βαρυτικά κύματα, που φθάνουν στη Γη από ένα κατακλυσμικό γεγονός στο μακρινό σύμπαν. Αυτό επιβεβαιώνει μια σημαντική πρόβλεψη του 1915 της Γενικής Θεωρίας της Σχετικότητας του Άλμπερτ Αϊνστάιν και ανοίγει ένα άνευ προηγουμένου νέο παράθυρο στο σύμπαν.

Τα βαρυτικά κύματα μεταφέρουν πληροφορίες σχετικά με τη δραματική προέλευσή τους και σχετικά με τη φύση της βαρύτητας που δεν μπορεί αλλιώς να αποκτηθεί. Οι φυσικοί έχουν καταλήξει στο συμπέρασμα ότι τα βαρυτικά κύματα που ανιχνεύτηκαν παράγονται κατά τη διάρκεια του τελικού κλάσματος του δευτερολέπτου της συγχώνευσης δύο μαύρων οπών σε μία ενιαία, πιο μαζική περιστρεφόμενη μαύρη τρύπα. Αυτή η σύγκρουση των δύο μαύρων τρυπών είχε προβλεφθεί, αλλά ποτέ δεν είχε παρατηρηθεί.

Τα βαρυτικά κύματα εντοπίστηκαν στις 14 Σεπτεμβρίου, 2015 5:51 πμ Ανατολική Ώρα (9:51 UTC) και από τα δύο δίδυμα συμβολόμετρα Laser του παρατηρητήριου βαρυτικών κυμάτων (LIGO), που βρίσκεται στο Λίβινγκστον της Λουιζιάνα, και Χάνφορντ στην Ουάσιγκτον , ΗΠΑ. Τα Παρατηρητήρια LIGO, που χρηματοδοτήθηκαν από το Εθνικό Ίδρυμα Επιστημών (NSF), σχεδιάστηκαν, κατασκευάστηκαν και λειτουργούν από το Caltech και το MIT. Η ανακάλυψη έγινε δεκτή για δημοσίευση στο περιοδικό Physical Review Letters και είναι αποτέλεσμα συνεργασίας του Παρατηρητηρίου Βαρυτικών Κυμάτων LIGO και της Virgo στην Ιταλία, που χρησιμοποιεί δεδομένα από τους δύο ανιχνευτές LIGO.

(περισσότερα…)

Ευθύγραμμη Κίνηση Online: Πολλαπλής Επιλογής

Online, Α΄ Λυκείου, Λύκειο, Χωρίς κατηγορία
Comments

Please go to Ευθύγραμμη Κίνηση Online: Πολλαπλής Επιλογής to view this quiz
Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

img_1494

Ευθύγραμμη Κίνηση Online: Σωστό – Λάθος

Online, Α΄ Λυκείου, Λύκειο
Comments

Please go to Ευθύγραμμη Κίνηση Online: Σωστό – Λάθος to view this quiz
Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

img_1494