Στις ασκήσεις που ακολουθούν να παίρνεις g=10m/s2.
- Ανάφερε τρεις περιπτώσεις μεταφοράς ενέργειας από ένα σώμα σε ένα άλλο.
- Δύναμη F επιταχύνει σώμα μάζας 5kg με επιτάχυνση 4m/s2 και το μεταφέρει σε απόσταση 20m. Υπολόγισε:
- Το έργο της F.
- Την ενέργεια που μεταβιβάζεται στο σώμα κατά τη μετακίνηση.
- Τροφοδοτούμε ένα σώμα μάζας 1kg με ενέργεια 200J μέσω του έργου δύναμης 50Ν.
- Πόσο διάστημα θα μετακινηθεί το σώμα;
- Πόση ταχύτητα θα αποκτήσει το σώμα;
- Μία οριζόντια δύναμη 80Ν κινεί ένα σώμα πάνω σε οριζόντιο επίπεδο με σταθερή ταχύτητα. Για μετατόπιση του σώματος κατά 5m:
- Πόση είναι η ενέργεια που μεταβιβάζεται στο σώμα από τη δύναμη των 80Ν και πού ξοδεύεται αυτή;
- Πόσο είναι το έργο της τριβής ολίσθησης;
- Ένα σώμα κινείται ευθύγραμμα με ενέργεια 500J. Για ένα διάστημα 3m ασκούμε σ’ αυτό δύναμη 100Ν με την ίδια κατεύθυνση της κίνησης. Πόση θα γίνει η ενέργεια του σώματος; Αν η δύναμη ασκηθεί με αντίθετη προς την κίνηση κατεύθυνση πάλι κατά 3m, πόση θα γίνει τότε η ενέργεια του σώματος;
- Σώμα βρίσκεται ακίνητο πάνω σε λεία οριζόντια επιφάνεια. Στο σώμα ασκείται μία δύναμη 30Ν, η οποία το μετακινεί κατά 2m. Αν η ενέργεια που προσφέρθηκε μέσω της δύναμης είναι 48J εξέτασε αν η κατεύθυνση της δύναμης είναι οριζόντια.
- Πόσο έργο χρειάζεται για να ανεβεί ένα ασανσέρ μάζας 800kg σε ύψος 12m; Αν στο ασανσέρ αυτό προσφέρουμε έργο 120.000J, πόσο ψηλά μπορεί να ανεβεί;
- Με τη βοήθεια κατακόρυφου νήματος τραβάμε προς τα πάνω μία σφαίρα μάζας 3kg για διάστημα 4m. Αν η σφαίρα αυξάνει την ταχύτητά της με ρυθμό 2m/s κάθε δευτερόλεπτο, υπολόγισε:
- Tο έργο της τάσης του νήματος.
- Το έργο του βάρους του σώματος.
- Την ενέργεια που μεταβιβάζεται από τη δύναμη στη σφαίρα.
- Πόση από την ενέργεια του ερωτήματος 3 καταναλώνεται από τη σφαίρα;
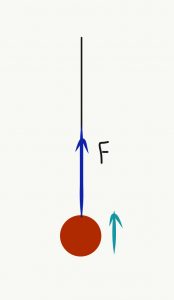
Άσκηση 8
- Βρες το έργο που εκτελείται από τη δύναμη που ασκείται σε κάθε σώμα της εικόνας.
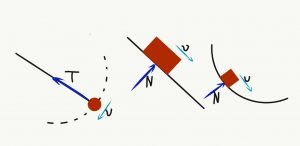
Άσκηση 9
- Ένα σώμα μάζας 20kg είναι ακίνητο πάνω σε λείο οριζόντιο επίπεδο. Κάποια στιγμή ασκείται στο σώμα μία οριζόντια δύναμη, οπότε, αφού διανύσει 40m, αποκτά ταχύτητα 20m/s. Πόση ενέργεια μεταφέρθηκε από τη δύναμη στο σώμα στο διάστημα των 40m;
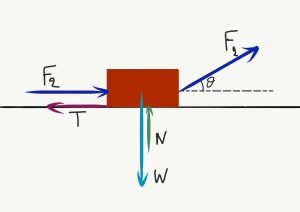
- Στο σώμα της εικόνας έχουμε F1=50N, F2=20N, w=100N, θ=300 και συντελεστή τριβής ολίσθηση μ=0,25. Το σώμα μετατοπίζεται κατά x=15m κατά την οριζόντια διεύθυνση. Υπολόγισε:
- Τη δύναμη N του δαπέδου επί του σώματος και την τριβή ολίσθησης Τ.
- Το έργο της κάθε δύναμης.
- Το συνολικό έργο όλων των δυνάμεων.
- Τη συνολική δύναμη ΣFx κατά τον άξονα x και τη ΣFy κατά τον άξονα y.
- Το έργο της συνισταμένης δύναμης.
Άσκηση 11
- Η δύναμη F ασκείται στο σώμα μάζας 12kg υπό γωνία 450 με κατεύθυνση προς τα κάτω. Το σώμα κινείται με σταθερή ταχύτητα για διάστημα 5m και ο συντελεστής τριβής ολίσθησης είναι μ=0,3. Πόσο είναι το έργο της δύναμης F;
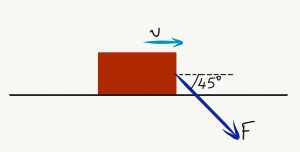
Άσκηση 12
- Ένα κιβώτιο 60kg το σέρνουμε στο οριζόντιο πάτωμα με μία οριζόντια δύναμη 200Ν. Ο συντελεστής της τριβής ολίθησης είναι μ=0,3. Βρες:
- Πόσο είναι το έργο που χρειάστηκε για να υπερβούμε την τριβή.
- Πόσο είναι το έργο που πήγε στην επιτάχυνση του κιβώτιου;
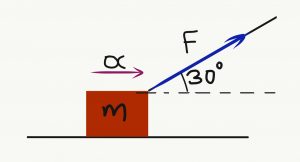
- Κιβώτιο μάζας 20kg βρίσκεται ακίνητο πάνω σε οριζόντιο επίπεδο. Με τη βοήθεια νήματος ασκούμε πάνω του δύναμη 100Ν υπό γωνία 300 με την οριζόντια διεύθυνση και το επιταχύνουμε με 3m/s2. Υπολόγισε:
- Το έργο που εκτελεί κάθε δύναμη που ασκείται πάνω στο κιβώτιο.
- Το συνολικό έργο όλων των δυνάμεων.
Άσκηση 14
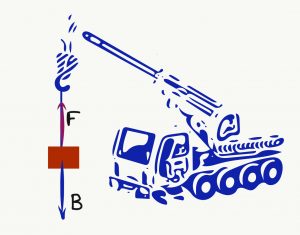
- Με τη βοήθεια γερανού ανυψώνουμε ένα κοντέινερ βάρους Β=5000Ν. Η ανυψωτική δύναμη του γερανού είναι F=6000Ν για τα πρώτα 6m και κατόπιν ελαττώνεται μέχρι να τοποθετηθεί το κοντέινερ σε ύψος 10m.
- Πόσο είναι το συνολικό έργο της ανυψωτικής δύναμης για να τοποθετηθεί το κοντέινερ στα 10m;
- Πώς κατανέμεται αυτό στα πρώτα 6m και στο υπόλοιπο της διαδρομής;
Άσκηση 15
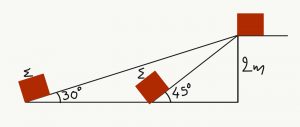
- Ένας εργάτης θέλει να ανεβάσει ένα βαρύ κιβώτιο σε ύψος 2m. Για το σκοπό αυτό έχει στη διάθεσή του δύο σανίδες, τις οποίες μπορεί να χρησιμοποιήσει σέρνοντας επάνω τους το κιβώτιο. Τη μία μπορεί να τη βάλει υπό γωνία 450 με το οριζόντιο επίπεδο και την άλλη υπό γωνία 300. Να συγκρίνεις το έργο που χρειάζεται να εκτελέσει ο εργάτης σε κάθε περίπτωση, όταν:
- Δε λάβουμε υπόψη τις τριβές του κιβωτίου με τις σανίδες.
- Ο συντελεστής τριβής μεταξύ του κιβώτιου και των σανίδων είναι μ.
Άσκηση 16
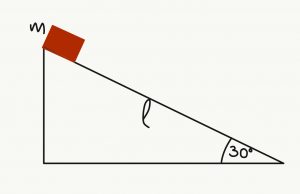
- Ένα σώμα μάζας 20kg αφήνεται να κινηθεί από την κορυφή κεκλιμένου επιπέδου γωνίας θ=300 και μήκους l=12m. Υπολόγισε το έργο που εκτελείται από κάθε δύναμη που ασκείται πάνω στο σώμα καθώς και το συνολικό έργο όλων των δυνάμεων, κατά την κίνηση του σώματος από την κορυφή προς τη βάση, όταν το κεκλιμένο επίπεδο:
- Δεν έχει τριβές.
- Έχει συντελεστή τριβής ολίσθησης με το σώμα μ=0,3.
Άσκηση 17
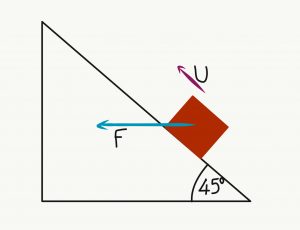
- Το σώμα έχει μάζα 10kg και βρίσκεται πάνω σε κεκλιμένο επίπεδο γωνίας 450 και μήκους l=2m. Με μία οριζόντια δύναμη F=200N, με κατεύθυνση προς τα αριστερά, σπρώχνουμε το σώμα προς τα πάνω επί του κεκλιμένου επιπέδου. Υπολόγισε το έργο που εκτελείται από κάθε δύναμη που ασκείται πάνω στο σώμα καθώς και το συνολικό έργο όλων των δυνάμεων, κατά την κίνηση του σώματος από τη βάση προς την κορυφή, όταν το κεκλιμένο επίπεδο:
- Δεν έχει τριβές.
- Έχει συντελεστή τριβής ολίσθησης με το σώμα μ=0,3.
Άσκηση 18
- Μία οριζόντια δύναμη θέτει σε κίνηση ένα σώμα μάζας m πάνω σε λεία οριζόντια επιφάνεια. Μετά από ορισμένο διάστημα το σώμα αποκτά ταχύτητα υ. Να αποδείξεις ότι το έργο της δύναμης είναι
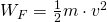 .
. - Πάνω σε οριζόντιο επίπεδο εκτοξεύουμε σώμα μάζας m με αρχική ταχύτητα υ0. Μετά από ορισμένο διάστημα το σώμα σταματάει. Να αποδείξεις ότι το έργο της τριβής είναι
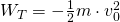 .
.
Γιάννης Γαϊσίδης
Visited 899 times, 1 visit(s) today
