Τοπίο στη Φυσική

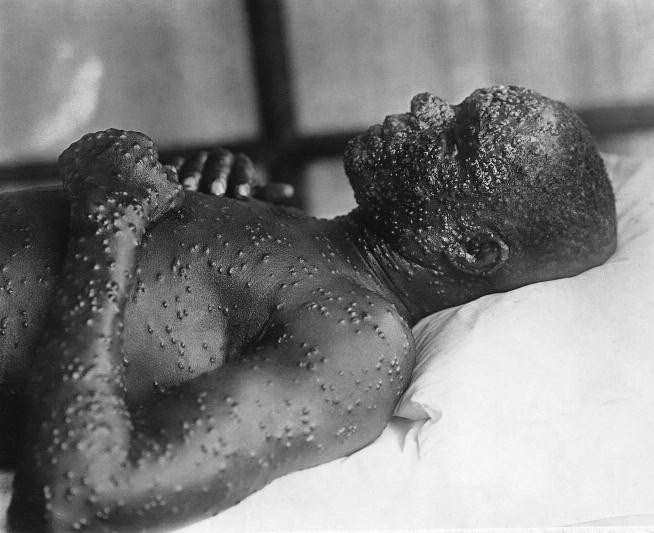
Ερευνητές σύντηξης στην Εθνική Εγκατάσταση Ανάφλεξης των Η.Π.Α. δημιούργησαν μια αντίδραση που παρήγαγε περισσότερη ενέργεια από όση έβαλαν

• Από τους Jeff Tollefson, Elizabeth Gibney, για το Nature magazine με αναδημοσίευση στο Scientific American

Οι επιστήμονες στη μεγαλύτερη εγκατάσταση πυρηνικής σύντηξης στον κόσμο πέτυχαν το φαινόμενο που είναι γνωστό ως ανάφλεξη – δημιουργώντας μια πυρηνική αντίδραση που παράγει περισσότερη ενέργεια από όση καταναλώνει. Τα αποτελέσματα της σημαντικής ανακάλυψης στην Εθνική Εγκατάσταση Ανάφλεξης των ΗΠΑ (NIF), που διεξήχθη στις 5 Δεκεμβρίου και ανακοινώθηκε στις 13 Δεκεμβρίου 2022 από την κυβέρνηση του προέδρου των ΗΠΑ Τζο Μπάιντεν, ενθουσίασαν την παγκόσμια ερευνητική κοινότητα σύντηξης. Αυτή η έρευνα στοχεύει να αξιοποιήσει την πυρηνική σύντηξη – το φαινόμενο που τροφοδοτεί τον Ήλιο – για να παρέχει μια πηγή σχεδόν απεριόριστης καθαρής ενέργειας στη Γη.

«Είναι ένα απίστευτο επίτευγμα», λέει ο Mark Herrmann, αναπληρωτής διευθυντής για θεμελιώδη φυσική όπλων στο Lawrence Livermore National Laboratory στην Καλιφόρνια, το οποίο στεγάζει το εργαστήριο σύντηξης. Το πείραμα ορόσημο έρχεται μετά από χρόνια εργασίας από πολλές ομάδες σε οτιδήποτε, από λέιζερ και οπτικά, έως στόχους και μοντέλα υπολογιστών, λέει ο Herrmann. «Φυσικά αυτό είναι που γιορτάζουμε».

Μια ναυαρχίδα πειραματικής εγκατάστασης του προγράμματος πυρηνικών όπλων του Υπουργείου Ενέργειας των ΗΠΑ που σχεδιάστηκε για να μελετά τις αντιδράσεις που δημιουργούνται από τέτοια όπλα, η NIF, είχε αρχικά στόχο να επιτύχει ανάφλεξη μέχρι το 2012 και αντιμετώπισε κριτική για καθυστερήσεις και υπερβάσεις κόστους. Τον Αύγουστο του 2021, επιστήμονες της NIF ανακοίνωσαν ότι είχαν χρησιμοποιήσει τη συσκευή τους λέιζερ υψηλής ισχύος για να επιτύχουν μια αντίδραση ρεκόρ, που ξεπέρασε ένα κρίσιμο όριο στην πορεία προς την ανάφλεξη, αλλά οι προσπάθειες να επαναλάβουν αυτό το πείραμα ή την κρούση τους επόμενους μήνες απέτυχαν. Τελικά, οι επιστήμονες ακύρωσαν τις προσπάθειες να αναπαραγάγουν αυτό το πλάνο και τους έκανε να ξανασκεφτούν τον πειραματικό σχεδιασμό – μια προσπάθεια που απέδωσε καρπούς την περασμένη εβδομάδα.

«Υπήρχαν πολλοί άνθρωποι που δεν πίστευαν ότι ήταν δυνατό, αλλά εγώ και άλλοι που κράτησαν την πίστη τους, νιώθουμε κάπως δικαιωμένοι», λέει ο Michael Campbell, πρώην διευθυντής του εργαστηρίου σύντηξης στο Πανεπιστήμιο του Ρότσεστερ στη Νέα Υόρκη και πρώιμος υποστηρικτής της NIF ενώ βρισκόταν στο εργαστήριο Lawrence Livermore. «Έχω ένα σύμπαν για να γιορτάσω».

Το Nature εξετάζει το τελευταίο πείραμα της NIF και τι σημαίνει για την επιστήμη της σύντηξης.

• Από το SCEPTIC Magazine, που εκδίδεται από τον οργανισμό SCEPTICS SOCIETY
• Του Daniel Loxton

To SCEPTIC SOCIETY είναι ένας μη κερδοσκοπικός μορφωτικός οργανισμός που προωθεί την επιστημονική γνώση, την κριτική σκέψη και ερευνά την ψευδοεπιστήμη και τα παραφυσικά φαινόμενα. Επικεφαλής και ιδρυτής του οργανισμού, στον οποίο μετέχουν πλήθος επιστημόνων, ερευνητών και δημοσιογράφων, είναι ο ακαδημαϊκός,καθηγητής του Chapman University, Michael Shermer, συγγραφέας επιστημονικών βιβλίων και ιστορίας της επιστήμης. Ένα από τα γνωστότερα βιβλία του είναι “Γιατί οι άνθρωποι πιστεύουν σε παράξενα πράγματα“, που έχει εκδοθεί από τις Πανεπιστημιακές Εκδόσεις Κρήτης, μεταφρασμένο στα Ελληνικά.

Το άρθρο που ακολουθεί δημοσιεύτηκε στο τεύχος του SCEPTIC Magazine και το αναδημοσιεύουμε, κατόπιν αδείας, στο site μας μεταφρασμένο. Είναι ένα εξαιρετικά ενδιαφέρον άρθρο μέσα από το οποίο μπορεί να μάθει κανείς την ιστορία των εμβολιασμών, αλλά και των αντιεμβολιαστικών κινημάτων σ’ αυτήν την ιδιαίτερα φορτισμένη κρίσιμη περίοδο.

Γιάννης Γαϊσίδης

Αιώνες Δυστυχίας

Θα μάθουμε πώς ανακαλύφθηκαν τα εμβόλια, πώς λειτουργούν και πώς σώζουν ζωές. Θα δούμε τρομακτικούς μύθους και θεωρίες συνωμοσίας για τα εμβόλια. Και θα διερευνήσουμε τη σκοτεινή πλευρά της ιστορίας των εμβολίων – γιατί ανεξάρτητα από το πόσο ασφαλές είναι κάτι, τα πράγματα μπορούν να πάνε ακόμα πιο στραβά.

Ας ξεκινήσουμε από την αρχή. Φανταστείτε για μια στιγμή πώς ήταν η ζωή πριν από χιλιάδες χρόνια, πριν υπάρξουν τα εμβόλια. Οι μεταδοτικές ασθένειες ήταν παντού. Εάν ζούσατε στην αρχαιότητα, η ζωή σας μπορεί να απειλούνταν από επιδημίες θανατηφόρων ασθενειών κάθε λίγα χρόνια. Η οικογένειά σας μπορεί να επιβίωνε ή να μολυνόταν, απλά για να αρρωστήσει και να πεθάνει στη συνέχεια. Σχεδόν όλοι έφεραν τη θλίψη από την απώλεια των αγαπημένων τους από μεταδοτικές ασθένειες.

Ακόμη χειρότερα, οι αρχαίοι άνθρωποι δεν καταλάβαιναν γιατί υπήρχαν οι ασθένειες. Κανείς δεν ήξερε ότι υπήρχαν μικρόβια. Μάντευαν αντ ‘αυτού ότι οι θεοί πρέπει να ήταν θυμωμένοι. Φαντάζονταν ότι οι ασθένειες στάλθηκαν για να τιμωρήσουν την ανθρωπότητα.

Σε προηγούμενη δημοσίευσή μας με τίτλο Η Φυσική πίσω από το πέταγμα της μποτίλιας παρουσιάσαμε μία ενδιαφέρουσα προσέγγιση της δημοφιλούς συνήθειας των μαθητών να πετούν τις πλαστικές φιάλες του νερού με σκοπό αυτές να προσγειωθούν κάθετα στην επιφάνεια του θρανίου τους. Το παρακάτω άρθρο από το American Journal of Physics παρουσιάζει μία πιο εμπεριστατωμένη και αναλυτική προσέγγιση του φαινομένου, μέσα από τη μελέτη πειραματικών και θεωρητικών δεδομένων, που λήφθηκαν από μία ομάδα προπτυχιακών φοιτητών του πανεπιστημίου Twente της Ολλανδίας.

• Των P. J. Dekker, L. A. G. Eek, M. M. Flapper, H. J. C. Horstink, A. R. Meulenkamp, and J. van der Meulen. Faculty of Science and Technology, University of Twente,The Netherlands
• Από το American Journal of Physics

Το ενδιαφέρον της μελέτης συνίσταται στην περιστροφή μιας φιάλης, μερικώς γεμάτης με νερό, που την προσγειώνουμε σε όρθια θέση. Είναι ένα εντυπωσιακό φαινόμενο, καθώς από την πρώτη ματιά φαίνεται μάλλον απίθανο ότι ένα ψηλό περιστρεφόμενο μπουκάλι θα μπορούσε να κάνει μια τέτοια σταθερή προσγείωση. Εδώ, αναλύουμε τη φυσική πίσω από την περιστροφή της φιάλης του νερού, με βάση πειράματα και ένα αναλυτικό μοντέλο που μπορεί να χρησιμοποιηθεί στην τάξη. Οι μετρήσεις μας δείχνουν ότι η γωνιακή ταχύτητα της φιάλης μειώνεται δραστικά, επιτρέποντας μια σχεδόν κάθετη κάθοδο και μια επιτυχημένη προσγείωση. Η μειωμένη περιστροφή οφείλεται σε αύξηση της ροπής αδράνειας που προκαλείται από την αναδιανομή της μάζας του νερού κατά τη διάρκεια της πτήσης κατά μήκος της φιάλης. Τα πειραματικά και αναλυτικά αποτελέσματα συγκρίνονται ποσοτικά και δείχνουμε πώς μπορούμε να βελτιστοποιήσουμε τις πιθανότητες επιτυχούς προσγείωσης.
(περισσότερα…)

Είναι βέβαιο ότι πολλές φορές, μέσα στην τάξη, κάνουμε παρατηρήσεις στους μαθητές, γιατί πετούν τα μπουκάλια τους με το νερό πάνω στο θρανίο σε έναν άτυπο διαγωνισμό μεταξύ τους, ποιος θα καταφέρει να το προσγειώσει κάθετα στην επιφάνεια του θρανίου. Ίσως η καταλληλότερη στιγμή για να ξεκινήσουμε μία συζήτηση, ποιοι νόμοι κρύβονται πίσω από το πέταγμα της μποτίλιας και πώς μπορούν να βελτιώσουν την τεχνική για να εντυπωσιάσουν τους συμμαθητές τους, είναι η στιγμή που τα βλέμματά τους στρέφονται στον συμμαθητή ή τη συμμαθήτριά τους, που κατάφερε να βάλει την μποτίλια όρθια, ενώ εμείς απτόητοι γράφουμε στον πίνακα το δεύτερο νόμο του Νεύτωνα για την περιστροφή των σωμάτων και πασχίζουμε να τον εξηγήσουμε. Το επόμενο βήμα είναι να τους ρίξουμε την ιδέα να διοργανώσουν ένα πρωτάθλημα για την ανάδειξη του μαθητή που θα καταφέρει να πετύχει τις περισσότερες κάθετες προσγειώσεις μέσα σε ένα αριθμό ρίψεων.

• Από το Scientific American

Το δημοφιλές βίντεο του μαθητή που πετάει μία μποτίλια με νερό και την προσγειώνει κάθετα στο τραπέζι.

Για να κατανοήσετε τη φυσική του πετάγματος της μποτίλιας, πρώτα πρέπει να καταλάβετε τη γωνιακή ορμή . Χωρίς πολλές λεπτομέρειες, πρόκειται για ένα γινόμενο δύο παραγόντων, της γωνιακής ταχύτητας ω (πόσο γρήγορα περιστρέφεται) και της ροπής αδράνειας Ι (πώς κατανέμεται η μάζα του γύρω από τον άξονα περιστροφής)  Όταν δεν υπάρχει εξωτερική ροπή στρέψης σε ένα αντικείμενο, ισχύει η αρχή διατήρησης της γωνιακής ορμής,  δηλαδή το γινόμενο της γωνιακής ταχύτητας και της ροπής αδράνειας παραμένει σταθερό. Κατά συνέπεια, αν το ένα από τα δύο αυξηθεί το άλλο θα πρέπει να μειωθεί ώστε να διατηρηθεί σταθερό το γινόμενό τους, δηλαδή η γωνιακή ορμή L. Ένα κλασικό παράδειγμα αυτού είναι μία περιστρεφόμενη αθλήτρια του πατινάζ στον πάγο. Αν αρχικά περιστρέφεται με τα χέρια της εκτεταμένα, έχει μια υψηλή ροπή αδράνειας, επειδή η μάζα της είναι απλωμένη, μακριά από τον άξονα περιστροφής της, που περνάει από το κέντρο μάζας της. Εάν τραβήξει τα χέρια της και τα φέρει σφιχτά στο σώμα της, η ροπή αδράνειας μειώνεται. Προκειμένου η γωνιακή ορμή της L να παραμείνει η ίδια, η γωνιακή της ταχύτητα πρέπει να αυξηθεί, ώστε να περιστρέφεται γρηγορότερα. Μπορείτε να παρατηρήσετε αυτό για τον εαυτό σας σε μια καρέκλα γραφείου που γυρίζει.

(περισσότερα…)

• Των Takeshi Asal, Takao Akatsuka και Steve Haake*
• Από το Physics World

Ο Bill Shankly, πρώην διευθυντής του ποδοσφαιρικού συλλόγου της Λίβερπουλ, είπε κάποτε: “Το ποδόσφαιρο δεν είναι θέμα ζωής και θανάτου. Είναι πιο σημαντικό από αυτά.” Αυτό το μήνα στο Παγκόσμιο Κύπελλο, εκατομμύρια φίλαθλοι θα νιώσουν το ίδιο συναίσθημα για λίγες, σύντομες εβδομάδες. Στη συνέχεια, η εκδήλωση θα τελειώσει και εκείνο που θα μείνει θα είναι μερικές επαναλήψεις στην τηλεόραση και η ατελείωτη εικασία για το τι θα μπορούσε να συμβεί. Είναι αυτή η πτυχή του ποδοσφαίρου που οι οπαδοί της αγαπούν και άλλοι μισούν. Τι θα γινόταν αν έμπαινε το πέναλτι; Τι θα συνέβαινε αν ο παίκτης δεν είχε αποβληθεί; Τι θα γινόταν αν το ελεύθερο λάκτισμα δε χτυπούσε στο τείχος και έμπαινε γκολ;

Ο Ρομπέρο Κάρλος της Βραζιλίας σκοράρει κατά της Γαλλίας με ένα τέλειο κτύπημα φάουλ.

Πολλοί οπαδοί θα θυμούνται το φάουλ που εκτέλεσε ο Βραζιλιάνος Ρομπέρτο Κάρλος σε ένα τουρνουά στη Γαλλία το 1997. Η μπάλα τοποθετήθηκε περίπου 30 μέτρα από την εστία του αντιπάλου και ελαφρώς δεξιά. Ο Κάρλος κτύπησε την μπάλα ξυστά στα δεξιά ώστε να περάσει αρχικά από το τείχος των αμυντικών κατά τουλάχιστον ένα μέτρο και να υποχρεώσει έναν ποδοσφαιριστή, που στεκόταν σε απόσταση μέτρια από το τέρμα, να σκύψει το κεφάλι του. Στη συνέχεια, σχεδόν μαγικά, η μπάλα έστριψε προς τα αριστερά και μπήκε στην πάνω δεξιά γωνία του γκολπόστ, προς μεγάλη έκπληξη των παικτών, του τερματοφύλακα και των μέσων μαζικής ενημέρωσης.

Προφανώς, ο Κάρλος εκτελούσε αυτό το λάκτισμα όλη την ώρα στο γήπεδο της προπόνησης. Ένιωθε διαισθητικά πώς να καμπυλώνει την μπάλα με το χτύπημα σε μια συγκεκριμένη ταχύτητα και με μία συγκεκριμένη περιστροφή. Πιθανότατα όμως δεν γνώριζε ότι πίσω από όλα ήταν η φυσική.

Αεροδυναμική των αθλητικών σφαιρών

Η πρώτη εξήγηση της πλευρικής κάμψης ενός περιστρεφόμενου αντικειμένου πιστώθηκε στο Λόρδο Rayleigh πάνω στην εργασία του Γερμανού φυσικού Gustav Magnus το 1852. Ο Magnus προσπαθούσε πραγματικά να προσδιορίσει γιατί περιστρεφόμενα κελυφοι και σφαίρες εκτρέπονται προς τη μία πλευρά αλλά η εξήγησή του ισχύει εξίσου καλά και με τις μπάλες. Πράγματι, ο θεμελιώδης μηχανισμός μιας μπάλας που καμπυλώνεται στο ποδόσφαιρο είναι σχεδόν ο ίδιος όπως σε άλλα αθλήματα όπως το μπέιζμπολ, το γκολφ, το κρίκετ και το τένις.

Περιστρεφόμενη μπάλα

Εξετάστε μια μπάλα που περιστρέφεται γύρω από έναν άξονα κάθετο στη ροή του αέρα και μέσα σ’ αυτόν (δείτε πάνω). Ο αέρας ταξιδεύει πιο γρήγορα σε σχέση με το κέντρο της σφαίρας εκεί όπου η περιφέρεια κινείται προς την ίδια κατεύθυνση με τη ροή του αέρα. Αυτό μειώνει την πίεση, σύμφωνα με την αρχή του Bernouilli. Το αντίθετο αποτέλεσμα συμβαίνει στην άλλη πλευρά της μπάλας, όπου ο αέρας ταξιδεύει πιο αργά σε σχέση με το κέντρο της μπάλας. Υπάρχει επομένως μια ανισορροπία στις δυνάμεις και η μπάλα εκτρέπεται – ή, όπως το έθεσε ο Sir J J Thomson το 1910, “η μπάλα ακολουθεί τη μύτη της”. Αυτή η πλευρική εκτροπή μιας μπάλας κατά την πτήση είναι γενικά γνωστή ως το “φαινόμενο Magnus”.

Οι δυνάμεις σε μια περιστρεφόμενη μπάλα που πετάει μέσα στον αέρα χωρίζονται γενικά σε δύο τύπους: τη δύναμη ανύψωσης και τη δύναμη αντίστασης. Η δύναμη ανύψωσης είναι η προς τα πάνω ή η προς τα πλάγια δύναμη που είναι υπεύθυνη για το φαινόμενο Magnus. Η δύναμη αντίστασης δρα στην αντίθετη κατεύθυνση από τη διαδρομή της μπάλας.

(περισσότερα…)

• Του J. Pantaleone
• Από το American Journal of Physics

ΠΕΡΙΛΗΨΗ

Όταν μια αλυσίδα ρέει πάνω από την άκρη ενός δοχείου και στη συνέχεια πέφτει κάτω στο έδαφος, παρατηρείται ότι η κορυφή της αλυσίδας ανεβαίνει πάνω από την άκρη του δοχείου. Αυτό ονομάζεται “πίδακας αλυσίδας” και είναι ένα διασκεδαστικό και αντιφατικό φαινόμενο. Σε αυτή την εργασία, αναλύεται πειραματικά και θεωρητικά η κίνηση σταθερής κατάστασης του πίδακα. Οι μετρήσεις δίνονται για τις ταχύτητες και τα ύψη για τρεις διαφορετικές αλυσίδες και τρεις διαφορετικές αποστάσεις από το δοχείο μέχρι το δάπεδο. Αποδεικνύεται ότι η απόσταση που η αλυσίδα ανυψώνεται πάνω από το δοχείο είναι ανάλογη της δύναμης από το δοχείο στην αλυσίδα. Ένα απλό μοντέλο αναπτύσσεται για τον τρόπο που η αλυσίδα αλληλεπιδρά με το δοχείο και δείχνει ότι ένας σύνδεσμος ανυψώνεται από το δοχείο μετά από περιστροφή με μια σχετικά μικρή γωνία. Οι προβλέψεις του μοντέλου συμφωνούν πολύ καλά με τις μετρήσεις για τις δύο αλυσίδες σφαιρών.

Ι. ΕΙΣΑΓΩΓΗ

Η κίνηση της πτώσης των αλυσίδων έχει μελετηθεί για μεγάλο χρονικό διάστημα. Οι αλυσίδες συχνά χρησιμοποιούνται ως παράδειγμα ενός συστήματος συνεχούς μάζας. Επιπλέον, οι πρόσφατες παρατηρήσεις έχουν βρει κάποια πολύ αντιφατικά αποτελέσματα. Για παράδειγμα, μια αλυσίδα που χτυπάει ένα τραπέζι μπορεί να επιταχυνθεί προς τα κάτω ταχύτερα από μια  αλυσίδα σε ελεύθερη πτώση.  Επίσης, όταν ένας σωρός αλυσίδας σε ένα τραπέζι τραβιέται γρήγορα οριζόντια, η αλυσίδα μπορεί να σηκωθεί αυθόρμητα για να σχηματίσει ένα τόξο πάνω από το τραπέζι. Το πιο εντυπωσιακό από όλα είναι το “πίδακας αλυσίδας”, επίσης γνωστό ως “αυτο-σιφόνιο χανδρών”. Σε ένα δημοφιλές βίντεο, ο Mould απέδειξε ότι μια αλυσίδα που πέφτει από ένα δοχείο μπορεί να ανεβεί αυθόρμητα σε ύψος και ότι η σταθεροποίηση του ύψους του μπορεί να είναι πολύ πάνω από το δοχείο, όπως φαίνεται στην Εικ. 1. Αυτή η εντυπωσιακή, αδιαμφισβήτητη επίδειξη παρέχει πολλές εκπαιδευτικές ευκαιρίες.

Εικ. 1. Ο πίδακας αλυσίδας

Ο βασικός φυσικός λόγος για τον οποίο συμβαίνει ο πίδακας είναι απλός. Όταν ένας σύνδεσμος σε κατάσταση ηρεμίας στο δοχείο έλκεται προς τα πάνω από την τάση στην ανερχόμενη αλυσίδα, αυτή η δύναμη επιταχύνει το κέντρο μάζας του συνδέσμου προς τα πάνω και προκαλεί επίσης την περιστροφή του συνδέσμου γύρω από το κέντρο μάζας. Η περιστροφή έχει ως αποτέλεσμα το άκρο του συνδέσμου που είναι σε επαφή με τον πάτο του δοχείου (ή με το σωρό της αλυσίδας) να ωθεί προς τα κάτω και έτσι να υπάρχει μια αντίστοιχη προς τα πάνω δύναμη “αντίδρασης” από το δοχείο στο σύνδεσμο. Αυτή η δύναμη αντίδρασης προκαλεί την ανύψωση της αλυσίδας πάνω από το δοχείο. Αν και η δύναμη αντίδρασης είναι ένα (σχετικά μικρό) κλάσμα της τάσης στην αλυσίδα του δοχείου, η τάση μπορεί να είναι μεγάλη όταν υπάρχει ένα μεγάλο μήκος αλυσίδας μεταξύ του δοχείου και του εδάφους. Όσο μεγαλύτερη είναι η απόσταση από το δοχείο μέχρι το πάτωμα, τόσο υψηλότερα πηγαίνει το τμήμα της αλυσίδας που υψώνεται πάνω από το δοχείο. (περισσότερα…)

The Physics Teacher Magazine (AAPT)

Του Eugene Hecht, Adelphi University, Garden City, NY

Όποιος έχει διδάξει εισαγωγική φυσική πρέπει να γνωρίζει ότι περίπου το ένα τρίτο των μαθητών αρχικά πιστεύει ότι οποιοδήποτε αντικείμενο σε κατάσταση ηρεμίας θα παραμείνει σε κατάσταση ηρεμίας, ενώ κάθε κινούμενο σώμα, στο οποίο δεν ασκούνται δυνάμεις, θα έρθει αμέσως σε ηρεμία. Ομοίως, περίπου οι μισοί από τους αμύητους μαθητές πιστεύουν ότι κάθε αντικείμενο που κινείται με σταθερή ταχύτητα πρέπει συνεχώς να το σπρώχνουμε, αν θέλουμε να διατηρεί την κίνησή του. Αυτό είναι ουσιαστικά ο νόμος του Αριστοτέλη για την κίνηση και είναι τόσο “προφανές” και επιβεβαιωμένο από την εμπειρία, ώστε ο νόμος αυτός έγινε αποδεκτός από τους μελετητές για 2000 χρόνια, ακριβώς μέχρι από την επανάσταση του Κοπέρνικου. Αλλά, φυσικά, είναι εντελώς λάθος. Το κείμενο αυτό αφηγείται την ιστορία τού πώς μπορούμε να κατανοήσουμε το νόμο της αδράνειας, πώς εξελίχθηκε και πώς ο Νεύτωνας κατέληξε να τον κάνει πρώτο του νόμο.

Ο Φιλόσοφος, η Ώθηση και ο Κέπλερ

Ο Αριστοτέλης (384-322 π.Χ.) ήταν τόσο αγαπητός κατά το Μεσαίωνα που ευλαβικά αναφερόταν ως “Ο Φιλόσοφος”. Ακόμα κι αν οι περισσότερες θεωρήσεις του επί της φυσικής ήταν λάθος, οι σχολαστικοί της εποχής ακολουθούσαν πεισματικά τις διδασκαλίες του. Γι αυτούς, και ως εκ τούτου για την Χριστιανοσύνη, η ουράνια περιοχή ήταν άπειρη και σχηματιζόταν από ένα πέμπτο τέλειο στοιχείο τον Αιθέρα. Ο χώρος ήταν γεμάτος, κενό δεν  μπορούσε να υπάρξει. Κάθε πρωταρχικό στοιχείο (φωτιά, γη, αέρας και νερό) είχε τη θέση του προς την οποία έτεινε να επιστρέψει. Κάθε γήινος βράχος είχε βαρύτητα και φυσικά έπεφτε προς στο κέντρο της Γης, το κέντρο του σύμπαντος. Κάθε άλλη κίνηση ήταν αφύσικη και απαιτούσε κάποια εξωτερική επίδραση. Ένας μηχανισμός έπρεπε συνεχώς να είναι σε επαφή με αυτό που κινείται. Εκτός από την πτώση, η ακινησία ήταν η προεπιλεγμένη (φυσιολογική) κατάσταση των υλικών πραγμάτων.
(περισσότερα…)