Έργο Βάρους και μεταβολή της Κ.Ε.

Τις ασκήσεις που ακολουθούν προσπάθησε να τις επιλύσεις εφαρμόζοντας το Θεώρημα Μεταβολής της Κινητικής Ενέργειας. Να λαμβάνονται υπόψιν οι τριβές και οι αντιστάσεις, εκτός αν δηλώνεται το αντίθετο. Επίσης να παίρνεις g=10m/s² .

Αθλητής του άλματος επί κοντώ περνάει πάνω από ύψος 5,80m. Αν η μάζα του είναι 80kg υπολόγισε:
1. Το έργο του βάρους του.
2. Την κινητική ενέργεια που θα έχει τη στιγμή που πέφτει στο στρώμα.
3. Την ταχύτητα με την οποία κουμπάει το στρώμα.
Άσκηση 1
Εκτοξεύουμε με το χέρι μας μικρή συμπαγή σφαίρα, κατακόρυφα προς τα πάνω, με ταχύτητα υ₀=8m/s.
1. Σε πόσο ύψος από το σημείο που την εκτοξεύσαμε τη σφαίρα χάνει το 50% της αρχικής της κινητικής ενέργειας;
2. Σε πόσο ύψος η ταχύτητά της μειώνεται κατά 50%;
3. Σε πόσο ύψος μπορεί να φτάσει η σφαίρα και σε πόσο χρόνο;
Οι τριβές θεωρούνται αμελητέες.
Από ύψος 13,2m πάνω από το έδαφος ρίχνουμε κατακόρυφα προς τα κάτω μικρό συμπαγές σώμα μάζας 5kg με ταχύτητα υ₀=5m/s.
1. Πόσο είναι το έργο του βάρους κατά την κίνησή του μέχρι το έδαφος;
2. Με πόση κινητική ενέργεια φτάνει στο έδαφος;
3. Πόσος χρόνος χρειάστηκε μέχρι να αγγίξει το έδαφος;
Οι τριβές θεωρούνται αμελητέες.
Σφαίρα μάζας 5kg ανεβαίνει προς τα πάνω με τη βοήθεια ενός σχοινιού. Μετά από διάστημα 4m η σφαίρα αποκτά ταχύτητα 8m/s. Πόσο είναι το έργο της δύναμης F που ασκεί το σχοινί στη σφαίρα για τη διαδρομή των 4m; Κατά τη διάρκεια της κίνησης, επί της σφαίρας ασκείται σταθερή δύναμη αντίστασης του αέρα F_αντ=10N.
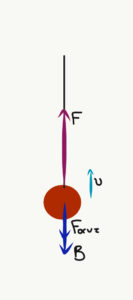
Άσκηση 4
Από ύψος 100m αφήνουμε να πέσει σώμα μάζας 20kg. Το σώμα φτάνει στο έδαφος με ταχύτητα 40m/s. Υπολόγισε:
1. Το έργο του βάρους.
2. Το έργο της αντίστασης του αέρα.
3. Με πόση ταχύτητα θα έφτανε στο έδαφος αν δεν υπήρχε αέρας;
Αθλητής της πτώσης με αλεξίπτωτο πέφτει από την κορυφή χαράδρας ύψους 200m και φτάνει στο έδαφος με ταχύτητα 6m/s. Ποιο είναι το ποσοστό του έργου του βάρους που χάθηκε από την αντίσταση του αέρα;
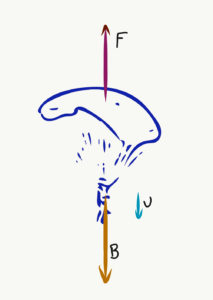
Άσκηση 5
Εκτοξεύουμε κατακόρυφα προς τα πάνω σώμα μάζας 2kg με ταχύτητα 15m/s. Σε πόσο ύψος από το σημείο της εκτόξευσης θα φτάσει το σώμα, αν ασκείται επάνω του η αντίσταστη του αέρα με σταθερό μέτρο F=10N; Σε πόσο χρόνο θα φτάσει στο μέγιστο ύψος;
Από την επιφάνεια του εδάφους εκτοξεύουμε κατακόρυφα προς τα πάνω σώμα μαζας 2kg με ταχύτητα υ₀=20m/s. Το σώμα φτάνει σε μέγιστο ύψος 8m και αρχίζει να πέφτει. Αν κατά τη διαρκεια της ανόδου και της καθόδου δέχεται αντίσταση από τον αέρα σταθερού μέτρου F, υπολόγισε:
1. Τη δύναμη αντίστασης F.
2. Την ταχύτητα με την οποία το σώμα επιστρέφει στο έδαφος.
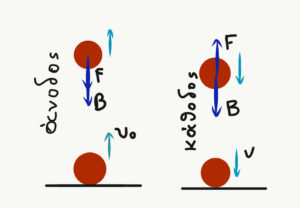
Άσκηση 5
Σώμα μάζας 4kg το αφήνουμε να πέσει στο στο έδαφος από ορισμένο ύψος. Ο χρόνος της πτώσης του είναι 5s και η ταχύτητα πρόσκρουσης στο έδαφος 40m/s, Από το θεώρημα μεταβολής της κινητικής ενέργειας υπολόγισε το έργο της αντίστασης του αέρα. Η δύναμη της αντίστασης είναι σταθερή.
Αφήνουμε από ύψος 50m να πέσει σώμα μάζας 4kg, οπότε η αντίσταση του αέρα καταναλώνει το 70% του έργου του βάρους. Με πόση ταχύτητα πρέπει να πετάξουμε κατακόρυφα προς τα πάνω το ίδιο σώμα ώστε να φτάσει στο σημείο από το οποίο αρχικά το αφήσαμε να πέσει; Η αντίσταση του αέρα παραμένει κατά μέτρο σταθερή και κατά την άνοδο και κατά την κάθοδο του σώματος.
Ποδοσφαιριστής σουτάρει φάουλ. Το πόδι του βρίσκεται σε επαφή με την μπάλα για 0,4m και ασκεί σ’ αυτή σταθερή δύναμη 700Ν. με πόση ταχύτητα φεύγει από το πόδι του η μπάλα; Η μάζα της μπάλας είναι 450gr.
Ένα σώμα έχει μάζα 20kg και βρίσκεται ακίνητο πάνω σε οριζόντια επιφάνεια. Ασκώντας επάνω του μία σταθερή οριζόντια δύναμη F, το θέτουμε σε κίνηση. Αν οι επιφάνειες που τρίβονται είναι λείες, τότε το σώμα αποκτά ταχύτητα 20m/s όταν διανύει 8m. Αν όμως είναι τραχείες, όταν διανύει και πάλι 8m, αποκτά ταχύτητα 15m/s. Πόση είναι η τριβή στην περίπτωση αυτή;
Αν θεωρήσουμε τις τριβές αμελητέες, πότε απαιτείται περισσότερο έργο, όταν θέλουμε να αυξήσουμε την ταχύτητα ενός αυτοκινήτου από 30Km/h σε 40km/h ή από 70km/h σε 80km/h;
Με ένα οριζόντιο σχοινί τραβάμε σώμα μάζας 5kg πάνω στο οριζόντιο επίπεδο. Η δύναμη που ασκείται στο σώμα από το σχοινί είναι F=60N. Μετά από 4m το σχοινί σπάει και το σώμα σταματάει, αφού διανύσει ορισμένο διάσυημα ακόμα. Αν ο συνετελεστής τριβής μεταξύ του σώματος και του οριζοντίου επιπέδου είναι μ=0,3 και το σώμα αρχικά ήταν ακίνητο, πόσο είναι το συνολικό διάστημα που διάνυσε το σώμα;
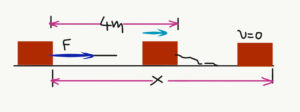
Άσκηση 14
Αθλητής των καταδύσεων εκτελεί βουτιά από βατήρα 10m. Αν το μέγιστο βάθος που φτάνει μέσα στην πισίνα είναι 4m, πόση είναι η αντίσταση που δέχεται από το νερό; Η μάζα του αθλητή είναι 60kg και η αντίσταση σταθερή.
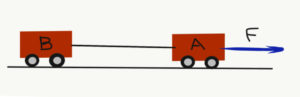
Τα βαγονάκια Α και Β είναι συνδεδεμένα με σχοινί. Aσκούμε στο Α οριζόντια δύναμη F=100N και θέτουμε το σύστημα σε κίνηση. Αν δεν υπάρχουν τριβές και οι μάζες είναι m_A=6N και m_B=4N, πόση είναι η τάση του σχοινιού; Υπόδειξη: Εφάρμοσε δύο φορές το Θεώρημα Μεταβολής της Κινητικής Ενεργειας. Μία για το ένα βαγονάκι και μία για το σύστημα και των δύο.
Άσκηση 16
Αυτοκίνητο τρέχει σε ευθεία οδό με ταχύτητα 72km/h. Ο οδηγός διαπιστώνει ότι σε απόσταση 70m υπάρχει πεσμένο στο δρόμο ένα δέντρο και φρενάρει για να αποφύγει τη σύγκρουση μ’ αυτό. Το αυτοκίνητο ολισθαίνει στο δρόμο όπου ο συντελεστής τριβής είναι 0,3. Θα αποφύγει τελικά τη σύγκρουση;
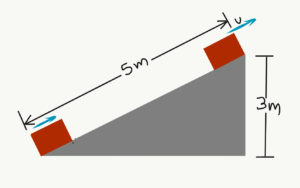
Από τη βάση κεκλιμένου επιπέδου βάλλεται προς τα πάνω και κατά μήκος του επιπέδου σώμα με αρχική ταχύτητα 14m/s. . Το σώμα φτάνει στην κορυφή του κεκλιμένου, αφού έχει διανύσει μηκος 5m και έχει ανεβεί κατά 3m. Αν ο συντελεστής τριβής είναι 0,4, υπολόγισε με πόση ταχύτητα φτάνει στην κορυφή.
Άσκηση 18
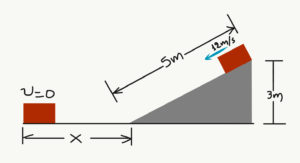
Από την κορυφή κεκλιμένου επιπέδου που βρίσκεται σε ύψιος 3m, βάλλεται κατά μήκος του και προς τα κάτω σώμα με ταχύτητα 12m/s. Το σώμα διανύει μήκος 5m επί του κεκλιμένου και συνεχίζει στο οριζόντιο επίπεδο. Υπολόγισε πόσο μήκος x θα κινηθεί επί του οριζόντιου επιπέδου μέχρι να σταματήσει, αν η συντελεστής τριβής σε όλη τη διαδρομή του είναι 0,4.
Άσκηση 19
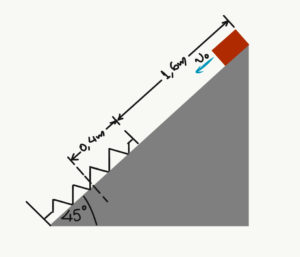
Από την κορυφή κεκλιμένου επιπέδου με γωνία κλίσης 45⁰, βάλλεται με αρχική ταχύτητα 6m/s, προς τα κάτω και κατά μήκος του επιπέδου, σώμα μάζας 10kg. Το σώμα, αφού διανύσει μήκος 1,6m, κτυπάει στην άκρη ενός ελατηρίου που είναι στερεωμένο στη βάση του κεκλιμένου επιπέδου και το συσπειρώνει κατά 0,4m. Πόσο είναι το έργο της δύναμης του ελατηρίου; Ο συνετελεστής τριβής μεταξύ του σώματος και του επιπέδου είνσι 0,4 και συν45⁰=0,7, ημ45⁰=0,7.
Άσκηση 20
Σε σώμα μάζας 4kg, που βρίσκεται στη βάση κεκλιμένου επιπέδου, ασκείται οριζόντια σταθερή δύναμη F=120Ν. Το σώμα αρχίζει να κινείται κατά μήκος του επιπέδου. Για πόσο μήκος πρέπει να ασκείται η F ώστε το σώμα να διανύσει συνολικά 10m μέχρι να σταματήσει και ταυτόχρονα να έχει ανεβεί κατά 6m; Ο συντελεστής τριβής σώματος-επιπέδου είναι 0,4.
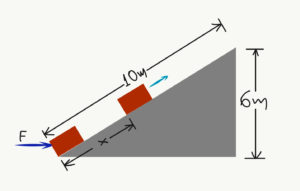
Άσκηση 21
Ένας σκιέρ αρχίζει την κάθοδό του από την κορυφή ενός λόφου με υψόμετρο 120m. Η κλίση του κεκλιμένου επιπέδου είναι 10⁰. Η συνολική μάζα του σκιέρ και του εξοπλισμού του είναι 80kg.
1. Χωρίς να λάβεις υπόψη τις τριβές και τις αντιστάσεις, πόση θα είναι η ταχύτητά του στη βάση του λόφου;
2. Αν τελικά ο αθλητής του σκι φτάνει στη βάση με μηδενική ταχύτητα, ποια θα είναι η μέση δύναμη της τριβής, συμπεριλαμβανομένης και της αντίστασης του αέρα;
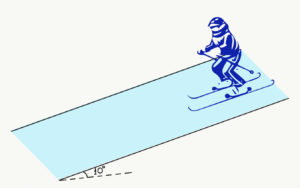
Άσκηση 22