Το πώς χρησιμοποιούμε το μαθηματικό φορμαλισμό μέσα στην τάξη, όσοι διδάσκουμε μαθήματα φυσικών επιστημών, είναι ένα τεράστιο κεφάλαιο, που ποτέ δε θα κλείσει. Πώς θα περάσουμε τη γνώση στους μαθητές μας; Θα παραμείνουμε πιστοί στην εννοιολογική μέθοδο; Θα βασιστούμε στη σιγουριά των μαθηματικών, για να δώσουμε απλές συνταγές επίλυσης; Ποιο είναι το ιδανικό μείγμα φυσικών και μαθηματικών γνώσεων; Το παρακάτω άρθρο του καθηγητή βιοεπιστημών Edward F. Redish μας κάνει μία εισαγωγή στο πρόβλημα, εντοπίζει τις διαφορές των καθαρών μαθηματικών από τα μαθηματικά για τις φυσικές επιστήμες και μας δίνει το έναυσμα για περαιτέρω προβληματισμό.
- Edward F. Redish
- Από το περιοδικό The Physics Teacher
Η βασική διαφορά μεταξύ των μαθηματικών ως μαθηματικών και των μαθηματικών στις φυσικές επιστήμες είναι ότι στις επιστήμες συνδυάζουμε τη φυσική μας γνώση με τις γνώσεις μας για τα μαθηματικά. Αυτή η ανάμειξη αλλάζει τον τρόπο που δίνουμε νόημα στα μαθηματικά και ακόμη και τον τρόπο που ερμηνεύουμε τις μαθηματικές εξισώσεις. Το να μάθουμε να σκεφτόμαστε τη φυσική με μαθηματικά, αντί απλώς να υπολογίζουμε, αυτό περιλαμβάνει μια σειρά από γενικές επιστημονικές δεξιότητες σκέψης, που συχνά θεωρούνται δεδομένες (και σπάνια διδάσκονται) στα μαθήματα φυσικής. Σε αυτό το άρθρο, δίνω μια επισκόπηση της ανάλυσής μου για αυτές τις πρόσθετες δεξιότητες.
Πολλές από τις ιδέες και τις μεθόδους που συζητώ εδώ αναπτύχθηκαν στο πλαίσιο της μελέτης της εισαγωγικής φυσικής με φοιτητές βιοεπιστημών—πρώτα, βασισμένη στην άλγεβρα της φυσικής και στη συνέχεια στη NEXUS/Physics, ένα εισαγωγικό μάθημα φυσικής σχεδιασμένο ειδικά για τις βιοεπιστήμες Οι μαθητές σε αυτές τις τάξεις συχνά αντιστέκονται στην ιδέα ότι τα συμβολικά μεγέθη στις φυσικές επιστήμες αντιπροσωπεύουν φυσικές μετρήσεις και όχι αριθμούς και ότι οι εξισώσεις αντιπροσωπεύουν σχέσεις και όχι τρόπους υπολογισμού.
Τα μαθηματικά στην επιστήμη είναι διαφορετικά από τα μαθηματικά στα μαθηματικά
Στις φυσικές επιστήμες, τα σύμβολα αντιπροσωπεύουν ένα μείγμα – ένα νοητικό συνδυασμό φυσικής γνώσης με γνώση του πώς συμπεριφέρεται ένα μαθηματικό στοιχείο, όπως μια μεταβλητή ή μια σταθερά. Η εξέταση μιας εξίσωσης μέσω ενός μεγενθυτικού φακού που συνδυάζει τη φυσική και τα μαθηματικά αλλάζει τον τρόπο που τη σκεφτόμαστε και τη χρησιμοποιούμε.
Για παράδειγμα, όταν ορίζουμε το ηλεκτρικό πεδίο ως ![]() , έχουμε κατά νου ότι το F δεν είναι απλώς μια αυθαίρετη μεταβλητή, αλλά η συγκεκριμένη ηλεκτρική δύναμη που αισθάνεται το δοκιμαστικό φορτίο q, ένα εννοιολογικό μείγμα φυσικής και μαθηματικών. Στα μαθηματικά, θα συμπεριλαμβάναμε ρητά την q-εξαρτημένη στην ετικέτα μας. Στη φυσική, συνήθως δεν το κάνουμε. Μάλλον, περιμένουμε από τον θεατή να ερμηνεύσει το σύμβολο ως κάτι φυσικό και επομένως να συνειδητοποιήσει ότι, όταν το q αλλάζει, το ίδιο συμβαίνει και με το F. Ως αποτέλεσμα, όταν αλλάζει το q, το E δεν αλλάζει, εκπλήσσοντας τους μαθητές.
, έχουμε κατά νου ότι το F δεν είναι απλώς μια αυθαίρετη μεταβλητή, αλλά η συγκεκριμένη ηλεκτρική δύναμη που αισθάνεται το δοκιμαστικό φορτίο q, ένα εννοιολογικό μείγμα φυσικής και μαθηματικών. Στα μαθηματικά, θα συμπεριλαμβάναμε ρητά την q-εξαρτημένη στην ετικέτα μας. Στη φυσική, συνήθως δεν το κάνουμε. Μάλλον, περιμένουμε από τον θεατή να ερμηνεύσει το σύμβολο ως κάτι φυσικό και επομένως να συνειδητοποιήσει ότι, όταν το q αλλάζει, το ίδιο συμβαίνει και με το F. Ως αποτέλεσμα, όταν αλλάζει το q, το E δεν αλλάζει, εκπλήσσοντας τους μαθητές.
- Τα μαθηματικά στις τάξεις των μαθηματικών τείνουν να αφορούν αριθμούς. Τα μαθηματικά στις φυσικές επιστήμες δεν κάνουν κάτι τέτοιο. Συνδυάζουν την εννοιολογική γνώση της φυσικής με τα μαθηματικά σύμβολα.
Τα μαθηματικά στις φυσικές επιστήμες αφορούν στις σχέσεις μεταξύ φυσικών μεγεθών που μετατρέπονται σε αριθμούς μέσω της μέτρησης. Ως αποτέλεσμα, οι ποσότητες στις φ. επιστήμες τείνουν να έχουν διαστάσεις και μονάδες. Αυτά πρέπει να αντιμετωπίζονται διαφορετικά από τους συνηθισμένους αριθμούς. Σε αντίθεση με τους συνηθισμένους αριθμούς, διαφορετικά είδη ποσοτήτων δεν μπορούν να εξισωθούν. Οι μαθητές αναρωτιούνται γιατί απαγορεύονται εξισώσεις όπως ![]() (και
(και ![]() ) αλλά επιτρέπεται η εξίσωση
) αλλά επιτρέπεται η εξίσωση ![]() .
.
Οι μαθητές συνήθως δεν μαθαίνουν να κάνουν αυτό το μείγμα στα μαθηματικά και οι περισσότεροι μαθητές στην εισαγωγική φυσική δεν έχουν εμπειρία με αυτό. Αυτή η ανάμειξη έχει πολλή δομή και έχει ως αποτέλεσμα διαφορές στους τρόπους που χρησιμοποιούμε τα σύμβολα στα μαθηματικά και στις φυσικές επιστήμες.
- Τα μαθηματικά στις τάξεις μαθηματικών τείνουν να χρησιμοποιούν έναν μικρό αριθμό συμβόλων με περιορισμένους τρόπους. Τα μαθηματικά στη φυσική χρησιμοποιούν πολλά σύμβολα με διαφορετικούς τρόπους—και το ίδιο σύμβολο μπορεί να έχει διαφορετικές σημασίες ανάλογα με το πλαίσιο.
Σε ένα τυπικό βιβλίο άλγεβρας ή λογισμού, θα βρείτε πολύ λίγες εξισώσεις με περισσότερα από ένα ή δύο σύμβολα και τείνουν να ακολουθούν μια προβλέψιμη σύμβαση — τα x, y, z και t θα είναι μεταβλητές. f, g και h θα είναι συναρτήσεις. Τα a, b και c θα είναι σταθερές. Σε ένα τυπικό βιβλίο φυσικής, σπάνια θα βρείτε μια εξίσωση με λιγότερα από τρία σύμβολα και συχνά θα βρείτε εξίσωση με έξι ή περισσότερα. Και δεν θα ακολουθήσουν τις μαθηματικές συμβάσεις. Αυτό κάνει τις εξισώσεις που χρησιμοποιούμε στη φυσική να φαίνονται άγνωστες στους μαθητές και αυξάνει το επίπεδο δυσφορίας τους.
- Τα σύμβολα στα μαθήματα φυσικών επιστημών συχνά φέρουν νόημα που αλλάζει τον τρόπο που ερμηνεύουμε την ποσότητα.
Στα καθαρά μαθηματικά δεν έχει σημασία πώς ονομάζουμε κάτι. Στις φ. επιστήμες έχει. Εδώ, επιλέγουμε ένα σύμβολο για μια μεταβλητή ή σταθερά για να μας δώσει μια υπόδειξη για το είδος της ποσότητας που μιλάμε. Χρησιμοποιούμε το m για τη μάζα και το t για το χρόνο – ποτέ το αντίστροφο. Ακόμη πιο μπερδεμένο είναι το γεγονός ότι χρησιμοποιούμε το ίδιο σύμβολο για να σημαίνουν διαφορετικά πράγματα. Στην τάξη μου, το σύμβολο Q μπορεί να σημαίνει θερμότητα, ηλεκτρικό φορτίο ή ογκομετρική ροή. Το T μπορεί να αντιπροσωπεύει την τάση, τη θερμοκρασία ή την περίοδο μιας ταλάντωσης.
Μπορείτε να πείτε, «Λοιπόν, εν τάξει. Αλλά η ερμηνεία εξαρτάται από το πλαίσιο. Τότε είναι προφανές τι εννοείς». Αυτό είναι αλήθεια. Αλλά η αναζήτηση του πλαισίου σημαίνει ότι ήδη συνδυάζετε τις γνώσεις σας για το τι σημαίνουν φυσικά τα σύμβολα με τις μαθηματικές σας γνώσεις. Οι εξισώσεις στη φυσική δεν αντιπροσωπεύουν μόνο την ποσοτική γνώση του φυσικού κόσμου. Μέσω του μείγματος, κωδικοποιούν τόσο τη φυσική εννοιολογική γνώση όσο και τη λειτουργική εξάρτηση.
- Στα εισαγωγικά μαθηματικά, τα σύμβολα τείνουν να αντιπροσωπεύουν είτε μεταβλητές είτε σταθερές. Στις φ. επιστήμες, έχουμε πολλά διαφορετικά είδη συμβόλων και μπορεί να αλλάξουν από σταθερές σε μεταβλητές, ανάλογα με το τι θέλουμε να κάνουμε.
Τα μαθηματικά στα μαθηματικά φαίνονται τόσο καθαρά. Μια μεταβλητή είναι μια μεταβλητή. Μια σταθερά είναι μια σταθερά. Στη φυσική, οι σταθερές μας μπορεί να είναι καθολικές σταθερές, παράμετροι, αρχικές συνθήκες. και μπορεί να επιλέξουμε να διαφορίσουμε σε σχέση με αυτά.
- Στα εισαγωγικά μαθηματικά, οι εξισώσεις αφορούν σχεδόν πάντα την επίλυση και τον υπολογισμό. Στη φυσική είναι συχνά η εξήγηση.
Κάθε εξάμηνο, έχω έναν ή δύο φοιτητές των οποίων τα σχόλια είναι περίπου: «Δεν εξηγεί αρκετά. Ξοδεύει πάρα πολύ χρόνο κάνοντας άλγεβρα στον πίνακα». Αυτοί οι μαθητές δεν έχουν καταλάβει κάτι που προσπαθώ να καταστήσω ξεκάθαρο (αλλά προφανώς δεν τα καταφέρνω για όλους τους μαθητές): Η εξαγωγή μιας εξίσωσης είναι μια εξήγηση, εάν βλέπετε τις εξισώσεις να φέρουν εννοιολογικό νόημα. Αυτό είναι κάτι που δεν είναι προφανές και δεν είναι εύκολο να μαθευτεί, ειδικά όταν άλλες τάξεις φυσικών επιστημών δεν χρησιμοποιούν μαθηματικά με αυτόν τον τρόπο.
Αυτές οι «μαθητικές δυσκολίες» είναι διαφορετικές από τις συνηθισμένες μαθητικές δυσκολίες για τις οποίες μπορεί να ανησυχούμε. Δεν είναι απλώς έλλειψη γνώσης, όπως το να ξεχνάμε πώς να διαιρέσουμε με ένα κλάσμα. Αυτά είναι πιο περίπλοκα και «μετα»—ένα άλλο επίπεδο, που επικαλύπτει όλα όσα κάνουν οι μαθητές. Πολλά από τη βιβλιογραφία στην εκπαίδευση της φυσικής έχουν να κάνουν με το να βοηθήσουμε τους μαθητές να κατανοήσουν καλύτερα τις έννοιες της φυσικής. Η εστίαση στις έννοιες μερικές φορές θεωρείται ως απομάκρυνση από τα μαθηματικά. Αλλά πώς πρέπει να σκεφτόμαστε τη σκέψη των μαθητών όταν η έννοια που πρέπει να μαθευτεί είναι θεμελιωδώς μαθηματική όσο και φυσική.
Αδικώ τα μαθηματικά;
Ξέρω ότι κάποιοι μαθηματικοί φυσικοί (και ίσως ακόμη και κάποιοι μαθηματικοί) θα παραπονεθούν ότι έχω κάνει τα μαθηματικά αχυράνθρωπο. Πολλά από τα πράγματα που λέω ότι δεν κάνουν τα μαθηματικά, ασφαλώς και τα κάνουν — σε πιο προχωρημένες τάξεις. Στην εισαγωγική φυσική, υπάρχουν μερικά ενδιαφέροντα «κρυμμένα» προχωρημένα μαθηματικά. Χρησιμοποιούμε μερικές πολύ εξελιγμένες μαθηματικές δομές σε μια εισαγωγική τάξη, επειδή περιμένουμε από τους μαθητές μας να τις ερμηνεύσουν όχι χρησιμοποιώντας φανταχτερά μαθηματικά, αλλά μέσω του συνδυασμού με την κοινή φυσική γνώση.
Για παράδειγμα, το γεγονός ότι οι διαστάσεις μιας εξίσωσης πρέπει να ταιριάζουν μπορεί να θεωρηθεί ως μια ασαφής θεωρητική πρόταση του τύπου: «εφόσον οι κλίμακες μέτρησης είναι αυθαίρετες, οι εξισώσεις πρέπει να μετασχηματιστούν με την ίδια αναπαράσταση του γινομένου των ομάδων κλίμακας». Ορίζοντας ένα διανυσματικό πεδίο μαθηματικά ορθά, προϋποθέτει από τους μαθητές να σκεφτούν να τοποθετήσουν ένα διανυσματικό χώρο σε κάθε σημείο του χώρου. Αυτό απαιτεί κάτι που είναι γνωστό ως περιγραφή του χώρου ως πολλαπλότητα και δημιουργία μιας εφαπτομένης δέσμης. Ναι!
Εννοείται, οι φυσικοί δεν χρειάζονται αυτά τα φανταχτερά μαθηματικά και δεν τα διδάσκουμε ακόμη και στα μαθήματα των μεγάλων τάξεων. Είναι προφανές ότι δεν έχει νόημα να εξισώνουμε μια απόσταση και έναν χρόνο (εκτός αν υποθέσουμε μια σταθερή ταχύτητα φωτός). Είναι προφανές τι σημαίνει να έχεις ένα διάνυσμα σε κάθε σημείο του χώρου. Είναι σαν ένας χάρτης καιρού που δείχνει την ταχύτητα του ανέμου. Αυτό είναι αλήθεια. Αλλά το κρίσιμο στοιχείο για να μπορέσουμε να κάνουμε έναν έλεγχο μονάδας ή να ορίσουμε ένα πεδίο Ε χωρίς τα φανταχτερά μαθηματικά είναι η οικοδόμηση του μείγματος — ο διανοητικός συνδυασμός φυσικής γνώσης με μαθηματικές αναπαραστάσεις. Αυτή η ανάμειξη δεν είναι ούτε προφανής ούτε εύκολη και πρέπει να διδαχθεί.
Ζητάω πάρα πολλά;
Αν είστε ένας έμπειρος εκπαιδευτικός στην εισαγωγική φυσική, μπορεί να αισθάνεστε κάποια αγωνία σε αυτό το σημείο. «Το πρόγραμμα σπουδών μου είναι ήδη γεμάτο! Δεν έχω χρόνο να διδάξω ένα σωρό νέα περιεχόμενα!». Σύμφωνοι. Αλλά δεν προτείνω την προσθήκη νέου περιεχομένου. Αντίθετα, λέω ότι, αν πιστεύουμε ότι είναι σημαντικό για τους μαθητές να μάθουν να χρησιμοποιούν τα μαθηματικά στην επιστήμη αποτελεσματικά, τότε πρέπει να διδάξουμε το περιεχόμενο που διδάσκουμε με διαφορετικό τρόπο.
Αυτοί οι νέοι μαθησιακοί στόχοι δεν προσθέτουν στο περιεχόμενο της τάξης. Εμφανίζονται σε όλα τα περιεχόμενα, προσδιορίζοντας στρατηγικές που έχουν γενική χρησιμότητα. Είναι νήματα, ένας τρόπος σκέψης που διασταυρώνει το περιεχόμενο που τρέχει σε όλη την τάξη, συνδέοντάς το με τεχνικές και τρόπους σκέψης, όπως το στημόνι και το υφάδι σε μια ύφανση (Εικ. 1).
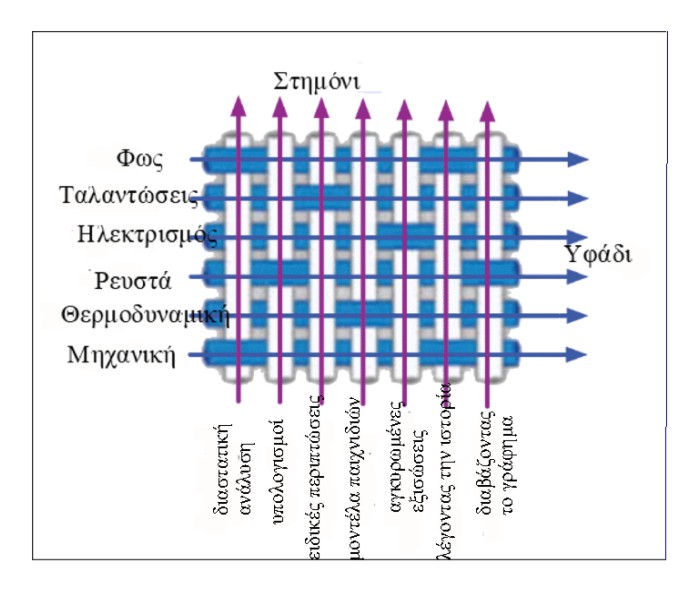
Αργότερα στην εργασία, θα παρουσιάσω μια σύντομη λίστα με μερικά από τα εργαλεία που χρησιμοποιώ για τη διδασκαλία της μαθηματικής σκέψης σε πολλαπλά πλαίσια. Αλλά πρώτα, χρειαζόμαστε μια βαθύτερη κατανόηση των εμποδίων που εμποδίζουν τους μαθητές να μάθουν αυτές τις δεξιότητες.
Αναλύοντας πώς σκέφτονται οι μαθητές
Όταν ζητάμε από τους μαθητές να κάνουν το είδος της «σκέψης με μαθηματικά» που περιγράφω, όχι μόνο τους βλέπουμε να δυσκολεύονται να το κάνουν, αλλά συχνά βρίσκουμε ισχυρή αντίσταση. Σε μια σειρά συνεντεύξεων με φοιτητές βιοεπιστημών σε ένα εισαγωγικό μάθημα φυσικής, οι Watkins και Elby τεκμηρίωσαν τις απόψεις ενός μαθητή για τα μαθηματικά στις φυσικές επιστήμες.
Ashlyn: Δεν μου αρέσει να σκέφτομαι τη βιολογία με όρους αριθμών και μεταβλητών. Νιώθω ότι για αυτό είναι η φυσική και ο λογισμός. Λοιπόν, εκείνο που εννοώ είναι ότι, όταν έρθει η ώρα για τις εξετάσεις, προφανώς θα κοιτάξω αυτές τις εξισώσεις, θα τις καταλάβω και θα τις απομνημονεύσω, αλλά δεν μου αρέσουν πραγματικά.
Η Ashlyn εκφράζει σημαντική δυσφορία με την προσπάθεια να χρησιμοποιήσει τις εξισώσεις για οτιδήποτε περισσότερο από υπολογισμό.
Από την άλλη πλευρά, σε ένα άλλο πλαίσιο, εκφράζει την ευχαρίστησή της που μαθαίνει στο μάθημα της βιολογίας (με μοντέλα και μαθηματικά) ότι η λειτουργική εξάρτηση του όγκου από το μέγεθος εξηγεί τον λόγο που δεν μπορούμε να έχουμε γιγάντια μυρμήγκια που είχε δει στο παρελθόν σε τηλεοπτικές σειρές.
Ashlyn: Ήξερα ότι δεν λειτουργεί όταν μεγαλώνεις τα μικρά πράγματα, αλλά ποτέ δεν είχα κανέναν να μου εξηγήσει ότι υπάρχει μια μαθηματική σχέση μεταξύ αυτού και αυτό ήταν πραγματικά χρήσιμο για τη γενική μου κατανόηση του κόσμου. Ήταν συγκλονιστικό…. Πραγματικά, μου τσάκισε το μυαλό.
Έχω δει και τις δύο αντιδράσεις της Ashlyn από πολλούς από τους μαθητές μου: αντίσταση στη χρήση των μαθηματικών για να σκέφτονται και όμως απολαμβάνουν όταν τα μαθηματικά τους επιτρέπουν να καταλάβουν κάτι που γνώριζαν αλλά δεν καταλάβαιναν γιατί ήταν έτσι.
Για να κατανοήσουμε αυτές τις πολυπλοκότητες των απαντήσεων των μαθητών, πρέπει να αναζητήσουμε τις βαθύτερες αιτίες της αντίστασης των μαθητών.
Η βασική ιδέα είναι ότι η γνώση έρχεται σε βασικά κομμάτια που αντλούνται από την εμπειρία στην καθημερινή ζωή καθώς και μέσω της σχολικής εκπαίδευσης. Αυτά τα κομμάτια γνώσης ενεργοποιούνται δυναμικά στον εγκέφαλο ως απόκριση τόσο σε εξωτερικά όσο και σε εσωτερικά ερεθίσματα.
Μερικές από τις διαφορές μεταξύ των μαθηματικών στα μαθηματικά και των μαθηματικών στις φ. επιστήμες, που απαρίθμησα παραπάνω, αφορούν στις προσδοκίες σχετικά με τη φύση της γνώσης της φυσικής –επιστημολογία– και κάποιες αφορούν στο είδος των πραγμάτων για τα οποία μιλάμε – την οντολογία.
Γνώση για τη γνώση-επιστημολογία
Όταν σκεφτόμαστε τις δυσκολίες των μαθητών με τα μαθηματικά στη φυσική, βοηθάει να σκεφτόμαστε τις προσδοκίες των μαθητών σχετικά με τη φύση της γνώσης που μαθαίνουν. Αυτά είναι εσωτερικά ερεθίσματα που καθοδηγούν και περιορίζουν τον τρόπο με τον οποίο οι μαθητές ανταποκρίνονται στη μάθηση στις τάξεις μας. Αυτές οι προσδοκίες μπορεί να περιλαμβάνουν ιδέες όπως, «Ξέρω ότι αυτό το μάθημα έχει να κάνει με την απομνημόνευση εξισώσεων. Απλώς πρέπει να βρω ποια εξίσωση έχει το σωστό σύμβολο» ή «Ξέρω ότι έχω κακή διαίσθηση για τη φυσική, επομένως πρέπει να εμπιστευτώ τα μαθηματικά μου ακόμα κι αν το αποτέλεσμα φαίνεται τρελό». Αναφέρομαι σε αυτό το είδος προσδοκίας ως επιστημολογία – γνώση για τη γνώση.
Οι επιστημολογικές προσδοκίες των μαθητών μπορούν να έχουν βαθιές επιπτώσεις σε αυτά που ακούν και πώς σκέφτονται για αυτά που μαθαίνουν. Συχνά κάνω μια σύντομη ερώτηση στις εξετάσεις μου. Αυτό με βοηθά να αποκτήσω μια ιδέα για το πώς σκέφτονται οι μαθητές πέρα από το «σωστό ή λάθος». Κάποτε, στις πρώτες μέρες μου, διδάσκοντας φυσική με βάση την άλγεβρα, στο τέλος του πρώτου εξαμήνου (νευτώνεια μηχανική), ρώτησα το εξής στην τελική εξέταση: «Ποια πιστεύετε ότι είναι η πιο σημαντική εξίσωση που μάθατε σε αυτό το μάθημα;» Προς αμηχανία μου, η πιο συνηθισμένη απάντηση ήταν ![]() . Ο δεύτερος νόμος του Νεύτωνα αναφέρθηκε σπάνια. Σαφώς έπρεπε να αλλάξω τον τρόπο που δίδασκα για τις εξισώσεις. Οι μαθητές μου έβλεπαν τις εξισώσεις ως καθαρά υπολογιστικά εργαλεία, όχι ως τρόπους για να τους βοηθήσω να σκεφτούν τη φυσική ή να οργανώσουν τις εννοιολογικές τους γνώσεις. Άλλαξα εντελώς την παρουσίασή μου για να επικεντρωθώ στους νόμους του Νεύτωνα ως πλαίσιο για τη μοντελοποίηση.
. Ο δεύτερος νόμος του Νεύτωνα αναφέρθηκε σπάνια. Σαφώς έπρεπε να αλλάξω τον τρόπο που δίδασκα για τις εξισώσεις. Οι μαθητές μου έβλεπαν τις εξισώσεις ως καθαρά υπολογιστικά εργαλεία, όχι ως τρόπους για να τους βοηθήσω να σκεφτούν τη φυσική ή να οργανώσουν τις εννοιολογικές τους γνώσεις. Άλλαξα εντελώς την παρουσίασή μου για να επικεντρωθώ στους νόμους του Νεύτωνα ως πλαίσιο για τη μοντελοποίηση.
Ένας χρήσιμος τρόπος να σκεφτούμε τις επιστημολογικές προσδοκίες των μαθητών είναι να εξετάσουμε τους βασικούς τρόπους με τους οποίους αποφασίζουν ότι γνωρίζουν κάτι: τους γνωσιολογικούς (επιστημολογικούς) πόρους τους. Αυτά μπορεί να είναι πράγματα που έμαθαν ως βρέφη («Ξέρω γιατί μου το είπε κάποιος που εμπιστεύτηκα») ή που τα έμαθαν στο σχολείο («Ξέρω γιατί έλυσα την εξίσωση και πήρα αυτήν την απάντηση.») Μερικές επιστημολογικές πηγές που θέλουμε οι μαθητές μας να μαθαίνουν στη φυσική περιλαμβάνουν:
- Ο χειρισμός συμβόλων που μπορεί να είναι αξιόπιστος — Τα αλγοριθμικά μετασχηματιστικά βήματα που ξεκινούν από μια εξίσωση εφαρμογής οδηγούν σε ένα αξιόπιστο αποτέλεσμα.
- Το φυσικό νόημα που μπορεί να αντιστοιχιστεί στα μαθηματικά — Μια μαθηματική συμβολική αναπαράσταση χαρακτηρίζει πιστά κάποιο χαρακτηριστικό του φυσικού ή γεωμετρικού συστήματος που προορίζεται να αναπαραστήσει.
- Εάν τα μαθηματικά είναι τα ίδια, η αναλογία είναι καλή — Τα μαθηματικά έχουν μια κανονικότητα και αξιοπιστία που είναι συνεπής σε διαφορετικές εφαρμογές.
- Τα μοντέλα παιχνιδιών που δίνουν διορατικότητα — Τα εξαιρετικά απλοποιημένα παραδείγματα μπορούν να δώσουν διορατικότητα σε περίπλοκη μαθηματική αναπαράσταση.
- Η συνέπεια είναι ζωτικής σημασίας — Όταν εξετάζετε ένα πρόβλημα με διαφορετικούς τρόπους, θα πρέπει να έχετε το ίδιο αποτέλεσμα. Αυτό είναι ιδιαίτερα πολύτιμο όταν μια φυσική και μαθηματική προοπτική μπορεί να τεθεί ανεξάρτητα, επιβεβαιώνοντας μια απάντηση στο μείγμα.
Σημειώστε ότι οι επιστημολογικοί πόροι, όπως αυτοί για τη φυσική γνώση, μπορεί να αντικρούονται μεταξύ τους. “Περισσότερα σημαίνει περισσότερα” μπορεί σωστά να υποδηλώνει ότι “ένα μεγαλύτερο αντικείμενο έχει περισσότερη αδράνεια και είναι πιο δύσκολο να κινηθεί”, αλλά “πιο κοντά είναι ισχυρότερο” σημαίνει ότι η λιγότερη απόσταση παράγει ένα μεγαλύτερο αποτέλεσμα όπως “πιο κοντά σε μια φωτιά είναι πιο ζεστό”, έτσι σε αυτή την περίπτωση «το λιγότερο είναι περισσότερο». Το τέχνασμα με τη χρήση πόρων για την επίλυση προβλημάτων είναι η δημιουργία συνεκτικών συντονισμένων συλλογών αυτών των πόρων και η ανάπτυξη κατανόησης των πλαισίων στα οποία είναι κατάλληλος το καθένας.
Γνώση για τα πράγματα — οντολογία
Ένα δεύτερο ζήτημα που είναι χρήσιμο για τον προβληματισμό σχετικά με τις δυσκολίες των μαθητών με τα μαθηματικά στη φυσική, είναι η οντολογία—η γνώση τους για το τι είδους πράγματα μιλάμε.
- Πολλές από τις έννοιές μας στη φυσική χωρίζουν κάτι που φαίνεται από φυσική άποψη σαν μια ενιαία έννοια, σε δύο μαθηματικές αναπαραστάσεις.
Για παράδειγμα, οι μαθητές συχνά αντιμετωπίζουν την «κίνηση» ως ένα μοναδικό πράγμα, αποτυγχάνοντας να διακρίνουν την ταχύτητα από την επιτάχυνση. Ενώ έχουν καλή φυσική εμπειρία τόσο με την κίνηση όσο και με την επιτάχυνση (πιάνοντας μια μπάλα ή αισθάνονται μια ώθηση προς τα πίσω όταν ένα όχημα επιταχύνει), η δημιουργία της σύνδεσης με τους ρυθμούς αλλαγής της τιμής της ταχύτητας, δεν είναι αυτόματη.
- Ορισμένες έννοιες στη φυσική δεν ταιριάζουν με τις απλές καθημερινές οντολογίες (π.χ. ύλη ή διαδικασία), αλλά απαιτούν μείγματα.
Κανείς δεν μας υποσχέθηκε ότι η φυσική επρόκειτο απλώς να κωδικοποιήσει την κοινή λογική! Η κβαντική φυσική είναι το πιο κραυγαλέα παράδειγμα, όπου η περιγραφή μας περιλαμβάνει χαρακτηριστικά που κάνουν τα αντικείμενα να μοιάζουν τόσο με σωματίδια (τοπική εκπομπή και απορρόφηση, διατήρηση ορμής σε συγκρούσεις, …) όσο και με κύμα (συμβολή, αρχή της αβεβαιότητας, …). Στην πραγματικότητα, υπάρχουν πολλά παραδείγματα επ’ αυτού, μερικά από αυτά ξεκάθαρα – όπως η αντιμετώπιση του φωτός ως ακτίνες, κύματα ή φωτόνια – και μερικά υπονοούμενα – όπως η εξέταση της ενέργειας από τη σκοπιά της ύλης (διατήρηση, πρέπει να είναι θετική τη τιμή της) και στις αναπαραστατικές της πτυχές (μπορεί να είναι αρνητική, να αντιμετωπίζεται ως ύψος πάνω ή κάτω από ένα σημείο αναφοράς).
- Ορισμένες από τις έννοιές μας στη φυσική ορίζονται μαθηματικά και μπορεί να μην έχουν προφανή φυσική αντιστοιχία.
Οι φυσικοί των σωματιδίων θα είναι εξοικειωμένοι με το γεγονός ότι τα θεμελιώδη πεδία (ή τα «στοιχειώδη σωματίδια») καθορίζονται ως προς το «τι είναι», προσδιορίζοντας πώς αποκρίνονται μαθηματικά σε διάφορους μετασχηματισμούς—την ομάδα περιστροφής (Τι είναι το σπιν του;), την ανταλλαγή σωματιδίων ( Είναι φερμιόνιο ή μποζόνιο;), και την ομάδα του Καθιερωμένου Μοντέλου, (Τι συγκεκριμένο σωματίδιο είναι;).
Αυτό το ίδιο είδος «η οντολογία ως μαθηματικά» συμβαίνει και στην εισαγωγική φυσική. Απλώς τείνουμε να μην το παρατηρούμε. Γίνεται προφανές όταν προσπαθούμε να εξηγήσουμε τι είναι ένα ηλεκτρικό πεδίο, χωρίς να συζητήσουμε τα διανυσματικά πεδία ή όταν προσπαθούμε να εξηγήσουμε, γιατί οι διασταυρωμένοι γραμμικοί πολωτές αφήνουν το φως να περάσει, όταν ένας γωνιακός γραμμικός πολωτής παρεμβάλλεται ανάμεσά τους, χωρίς να μιλάμε για διανύσματα και την αποσύνθεσή τους. Ίσως να μπορέσετε να το κάνετε αυτό (εγώ δεν μπορώ), αλλά είναι σαν να προσπαθείτε να παίξετε συλλαβογρίφους με τα χέρια δεμένα πίσω από την πλάτη σας.
Μια ζώνη εργαλείων για τα μαθηματικά των φυσικών επιστημών
Αυτή η ανάλυση των δυσκολιών που αντιμετωπίζουν οι μαθητές στο συνδυασμό των μαθηματικών με τις φυσικές επιστήμες εγείρει πολλά ερωτήματα. Τα επιστημολογικά και οντολογικά ζητήματα είναι μετα – διατρέχουν πολλά από τα συγκεκριμένα θέματα περιεχομένου που διδάσκουμε. Όταν εστιάζουμε μόνο στη λίστα των θεμάτων φυσικής που «καλύπτουμε», μπορεί να χάσουμε τις γενικότερες δεξιότητες που θέλουμε να αναπτύξουν οι μαθητές στην πορεία. Οι ειδικοί της φυσικής καταφέρνουν να μάθουν αυτές τις δεξιότητες, αλλά συχνά μετά από πολλά χρόνια (ή και δεκαετίες).
Η κατανόηση αυτών των βαθύτερων ζητημάτων σχετικά με τη φύση των γνώσεων και των εννοιών της φυσικής είναι ακόμη πιο σημαντική για τους μη προχωρημένους σπουδαστές φυσικής από οποιοδήποτε συγκεκριμένο περιεχόμενο που θα μπορούσαμε να επιλέξουμε να διδάξουμε. Αλλά οι μαθητές μας του «έχω να πάρω τη φυσική μόνο για ένα έτος» τείνουν να επικεντρώνονται στο «απλώς να τα καταφέρουν» και, εάν είναι στο πρώτο έτος της ιατρικής, να βεβαιωθούν ότι θα έχουν καλή βαθμολογία στις ΕΞΕΤΑΣΕΙΣ. Πολύ λίγοι θα κάνουν την προσπάθεια να σκεφτούν βαθιά αυτά που μαθαίνουν. Αν εκτιμούμε ότι πρέπει να τους μάθουμε να χρησιμοποιούν τα μαθηματικά ως επιστήμονες, πρέπει να βρούμε τρόπους να τα διδάξουμε με σαφήνεια στους μαθητές μας.
Το κλειδί είναι να διδάξουμε τους εισαγωγικούς μαθητές της φυσικής να κάνουν τη μετάβαση από τα μαθηματικά, ως επιστήμη των αριθμών, στα μαθηματικά ως εργαλείο για να σκεφτούν τη φυσική. Για να το κάνω αυτό, έχω αναπτύξει ένα σύνολο στρατηγικών γενικού σκοπού που ονομάζω «επιστημονικά παιχνίδια» ή «ηλεκτρονικά παιχνίδια», για συντομία: συγκεκριμένες προσεγγίσεις που μπορούν να εφαρμοστούν σε μια ποικιλία προβλημάτων. Περιγράφω την εκμάθηση του τρόπου εργασίας ως ανάπτυξη της μαθηματικής σας ζώνης εργαλείων. Δεν διδάσκω μόνο αυτές τις μεθόδους ρητά, αλλά κάθε μέθοδος έχει ένα συγκεκριμένο εικονίδιο εργαλείου. Κάθε φορά που χρησιμοποιώ ένα εργαλείο στην τάξη, το εικονίδιό του εμφανίζεται στη διαφάνεια.
Εδώ είναι μερικά από τα ηλεκτρονικά παιχνίδια που έχουμε αναπτύξει η ομάδα μου και εγώ.
- Διαστατική ανάλυση
- Υπολογισμός
- Εξισώσεις αγκύρωσης
- Μοντέλα παιχνιδιών
- Λειτουργική εξάρτηση
- Διαβάζοντας τη φυσική σε ένα γράφημα
- Λέγοντας την ιστορία
*Για περαιτέρω μελέτη μπορείτε να αναζητήσετε άρθρα του συγγραφέα Edward F. Redish στα επιστημονικά περιοδικά The Physics Teacher και Amarican Journal of Physics.
ΕΚΠΛΗΚΤΙΚΗ ΠΡΟΣΕΓΓΙΣΗ ΤΟΥ ΘΕΜΑΤΟΣ.ΜΕ ΠΡΟΒΛΗΜΑΤΙΣΕΣ ΠΟΛΥ.