Μία ποσοτική ανάλυση του πίδακα αλυσίδας

Του J. Pantaleone
Από το American Journal of Physics

ΠΕΡΙΛΗΨΗ

Όταν μια αλυσίδα ρέει πάνω από την άκρη ενός δοχείου και στη συνέχεια πέφτει κάτω στο έδαφος, παρατηρείται ότι η κορυφή της αλυσίδας ανεβαίνει πάνω από την άκρη του δοχείου. Αυτό ονομάζεται “πίδακας αλυσίδας” και είναι ένα διασκεδαστικό και αντιφατικό φαινόμενο. Σε αυτή την εργασία, αναλύεται πειραματικά και θεωρητικά η κίνηση σταθερής κατάστασης του πίδακα. Οι μετρήσεις δίνονται για τις ταχύτητες και τα ύψη για τρεις διαφορετικές αλυσίδες και τρεις διαφορετικές αποστάσεις από το δοχείο μέχρι το δάπεδο. Αποδεικνύεται ότι η απόσταση που η αλυσίδα ανυψώνεται πάνω από το δοχείο είναι ανάλογη της δύναμης από το δοχείο στην αλυσίδα. Ένα απλό μοντέλο αναπτύσσεται για τον τρόπο που η αλυσίδα αλληλεπιδρά με το δοχείο και δείχνει ότι ένας σύνδεσμος ανυψώνεται από το δοχείο μετά από περιστροφή με μια σχετικά μικρή γωνία. Οι προβλέψεις του μοντέλου συμφωνούν πολύ καλά με τις μετρήσεις για τις δύο αλυσίδες σφαιρών.

Ι. ΕΙΣΑΓΩΓΗ

Η κίνηση της πτώσης των αλυσίδων έχει μελετηθεί για μεγάλο χρονικό διάστημα. Οι αλυσίδες συχνά χρησιμοποιούνται ως παράδειγμα ενός συστήματος συνεχούς μάζας. Επιπλέον, οι πρόσφατες παρατηρήσεις έχουν βρει κάποια πολύ αντιφατικά αποτελέσματα. Για παράδειγμα, μια αλυσίδα που χτυπάει ένα τραπέζι μπορεί να επιταχυνθεί προς τα κάτω ταχύτερα από μια αλυσίδα σε ελεύθερη πτώση. Επίσης, όταν ένας σωρός αλυσίδας σε ένα τραπέζι τραβιέται γρήγορα οριζόντια, η αλυσίδα μπορεί να σηκωθεί αυθόρμητα για να σχηματίσει ένα τόξο πάνω από το τραπέζι. Το πιο εντυπωσιακό από όλα είναι το “πίδακας αλυσίδας”, επίσης γνωστό ως “αυτο-σιφόνιο χανδρών”. Σε ένα δημοφιλές βίντεο, ο Mould απέδειξε ότι μια αλυσίδα που πέφτει από ένα δοχείο μπορεί να ανεβεί αυθόρμητα σε ύψος και ότι η σταθεροποίηση του ύψους του μπορεί να είναι πολύ πάνω από το δοχείο, όπως φαίνεται στην Εικ. 1. Αυτή η εντυπωσιακή, αδιαμφισβήτητη επίδειξη παρέχει πολλές εκπαιδευτικές ευκαιρίες.

Εικ. 1. Ο πίδακας αλυσίδας

Ο βασικός φυσικός λόγος για τον οποίο συμβαίνει ο πίδακας είναι απλός. Όταν ένας σύνδεσμος σε κατάσταση ηρεμίας στο δοχείο έλκεται προς τα πάνω από την τάση στην ανερχόμενη αλυσίδα, αυτή η δύναμη επιταχύνει το κέντρο μάζας του συνδέσμου προς τα πάνω και προκαλεί επίσης την περιστροφή του συνδέσμου γύρω από το κέντρο μάζας. Η περιστροφή έχει ως αποτέλεσμα το άκρο του συνδέσμου που είναι σε επαφή με τον πάτο του δοχείου (ή με το σωρό της αλυσίδας) να ωθεί προς τα κάτω και έτσι να υπάρχει μια αντίστοιχη προς τα πάνω δύναμη “αντίδρασης” από το δοχείο στο σύνδεσμο. Αυτή η δύναμη αντίδρασης προκαλεί την ανύψωση της αλυσίδας πάνω από το δοχείο. Αν και η δύναμη αντίδρασης είναι ένα (σχετικά μικρό) κλάσμα της τάσης στην αλυσίδα του δοχείου, η τάση μπορεί να είναι μεγάλη όταν υπάρχει ένα μεγάλο μήκος αλυσίδας μεταξύ του δοχείου και του εδάφους. Όσο μεγαλύτερη είναι η απόσταση από το δοχείο μέχρι το πάτωμα, τόσο υψηλότερα πηγαίνει το τμήμα της αλυσίδας που υψώνεται πάνω από το δοχείο.

Ένα πράγμα που κάνει τον πίδακα αλυσίδας μια τόσο καλή εκπαιδευτική επίδειξη είναι ότι μπορεί να εξηγηθεί χρησιμοποιώντας απλούστερα φυσικά παραδείγματα. Συγκεκριμένα, η αλληλεπίδραση μεταξύ του δοχείου και του συνδέσμου που απομακρύνεται από αυτό, μπορεί να απεικονισθεί άμεσα με ένα πείραμα βολής πάνω σε ένα κομμάτι ξύλου. Εξετάστε τι συμβαίνει όταν μια σφαίρα προς τα πάνω χτυπά ένα κομμάτι ξύλου που βρίσκεται πάνω σε μια οριζόντια επιφάνεια. Το ξύλο θα ανυψωθεί πιο πολύ όταν η σφαίρα το χτυπήσει κοντά στην άκρη σε σύγκριση με την ανύψωση όταν η σφαίρα το χτυπά στο κέντρο. Η εξήγηση εδώ είναι πανομοιότυπη με τον πίδακα αλυσίδας και βασίζεται στο γεγονός ότι η δύναμη αντίδρασης από την οριζόντια επιφάνεια που περιστρέφει το κομμάτι ξύλου, ωθεί το ξύλο υψηλότερα. Το βίντεο αυτής της επίδειξης συμπεριλαμβάνει και μια συζήτηση για το πώς σχετίζεται ο πίδακας αλυσίδας με το ξύλο που βάλλεται από τη σφαίρα.Αυτή η συζήτηση κάνει την επίδειξη προσβάσιμη σε όλα τα επίπεδα των μαθητών φυσικής.

Υπάρχουν μόνο λίγες δημοσιευμένες εργασίες που συζητούν τον πίδακα αλυσίδας. Οι αρχικές εργασίες των Biggins και Warner εξήγησαν το βασικό λόγο για την ανύψωση της αλυσίδας πάνω από το δοχείο, μέτρησαν πόσο ψηλά ανυψώθηκε, ως συνάρτηση της απόσταση του δοχείου από το πάτωμα και ανέπτυξαν ένα απλό μοντέλο για να περιγράψουν τα αποτελέσματα. Με μια άλλη εργασία στη συνέχεια, ο Biggins περιέγραψε το σχηματισμό του πίδακα και την τιμή στην οποία προσέγγιζε τη σταθερή κατάσταση. Πιο πρόσφατα, οι Andrew κ.ά έχουν παρατηρήσει τον πίδακα για πολύ μεγάλες αλυσίδες και αναφέρουν μια μη γραμμική σχέση μεταξύ του ύψους ττου πίδακα και του ύψους της πτώσης.

Σε αυτή την εργασία, η σταθερή κατάσταση της αλυσίδας αναλύεται ποσοτικά. Το τμήμα ΙΙ περιέχει τις παρατηρήσεις μας για τους πίδακες με μετρημένα ύψη και ταχύτητες σταθερής κατάστασης για τρεις διαφορετικές αλυσίδες, δύο αλυσίδες μπάλας και μία αλυσίδα ράβδων. Το κεφάλαιο ΙΙΙ περιέχει το θεωρητικό μας μοντέλο που περιγράφει τον πίδακα αλυσίδας. Ένα γενικό πλαίσιο για τις δυνάμεις περιγράφεται στο Κεφ. III A και παράγεται ένας τύπος που συνδέει την ταχύτητα της αλυσίδας με τα ύψη ανόδου και πτώσης της αλυσίδας. Επίσης, αυτή η ενότητα δείχνει ότι η αλληλεπίδραση μεταξύ του δοχείου και του συνδέσμου που ανυψώνεται είναι κρίσιμη για την ανύψωση της αλυσίδας πάνω από το δοχείο. Αυτή η αλληλεπίδραση εξετάζεται λεπτομερώς στο Κεφ. ΙΙΙ Β. Εδώ, προκύπτουν τύποι για το ύψος που η αλυσίδα ανυψώνεται πάνω από το δοχείο και για την κρίσιμη γωνία του συνδέσμου σε σχέση με το πλάτος και το μήκος των αλυσίδων. Οι προβλέψεις του μοντέλου συμφωνούν ικανοποιητικά με τα μετρούμενα αποτελέσματα για τις δύο αλυσίδες σφαιρών. Για την αλυσίδα βάβδων, οι προβλέψεις είναι πολύ λιγότερο ακριβείς, αλλά εξηγείται ο λόγος της απόκλισης. Το τμήμα IV εξετάζει επιπρόσθετες φυσικές επιδράσεις και επίσης διαφορετικούς τρόπους με τους οποίους μπορεί να χρησιμοποιηθεί ο πίδακας αλυσίδας για τη διδασκαλία. Τέλος, το τμήμα V παρέχει μια σύντομη περίληψη των αποτελεσμάτων.

ΙΙ. ΠΑΡΑΤΗΡΗΣΕΙΣ

Ένας τυπικός πίδακας αλυσίδας φαίνεται στην Εικ. 1. Το σχήμα της αλυσίδας αποτελείται από σχετικά ευθείες κάθετες πλευρές με ένα μικρό καμπύλο τμήμα στην κορυφή. Είναι σύνηθες για τα κύματα να διαδίδονται κατά μήκος της αλυσίδας (βλέπε αριστερή πλευρά της Εικ. 1) και κοντά στην κορυφή μια ομαλή καμπύλη να έχει μικρές παραμορφώσεις σχετικά μακράς διαρκείας. Το μέγιστο ύψος της αλυσίδας παρουσιάζει διακυμάνσεις λόγω διαφόρων συνθηκών στο δοχείο. Για παράδειγμα, τα μπερδέματα ή τα χτυπήματα στο δοχείο μειώνουν προσωρινά το ύψος.

Οι παρατηρήσεις που αναφέρθηκαν εδώ έγιναν χρησιμοποιώντας τρεις διαφορετικές αλυσίδες: αλυσίδα μικρής σφαίρας, αλυσίδα μεγάλης σφαίρας και αλυσίδα βάβδου (βλ. Εικ. 2). Οι μπάλες και οι ράβδοι είναι κούφιες και συνδέονται με μικρές μπάρες που φουσκώνουν στα άκρα. Και για τις τρεις αλυσίδες η μέγιστη γωνία κάμψης σε μια ένωση μεταξύ μπάρας και σφαίρας / ράβδου ήταν περίπου 20 °. Ωστόσο, λόγω της γεωμετρίας σύνδεσης, όσο μεγαλύτερη είναι η γωνία κάμψης τόσο περισσότερο πρέπει να ολισθήσει η μπάρα μέσα στη σφαίρα / ράβδο. Η αλυσίδα ράβδου και η αλυσίδα μεγάλης σφαίρας είχαν μήκος περίπου 30m, ενώ η μικρή αλυσίδα είχε μήκος 75m. Οι φυσικές παράμετροι αυτών των αλυσίδων δίδονται στον πίνακα Ι (βλέπε Εικ. 3 για τους ορισμούς των μηκών).

Εικ. 2. Φωτογραφία των αλυσίδων που χρησιμοποιήθηκαν σ’ αυτό το πείραμα.

Πίνακας Ι. Φυσικές παράμετροι των τριών αλυσίδων. Σε όλες τις αλυσίδες, λ είναι η γραμμική πυκνότητα μάζας. Για την αλυσίδα μπάλας D και L είναι οι διαστάσεις των αλυσίδων όπως ορίζονται στην Εικ. 3. Για την αλυσίδα ράβδου, ως σύνδεσμος ορίζονται δύο ράβδοι που συνδέονται μεταξύ τους με μια μικρή μπάρα. Μια ράβδος παριστάνεται από δύο ημισφαίρια διαμέτρου D διαχωρισμένα από ένα κύλινδρο μήκους S και με L ορίζεται η απόσταση μεταξύ των εξωτερικών ημισφαιρίων του συνδέσμου, έτσι L = 2S + D + το μήκος της μπάρας σύνδεσης. Η ποσότητα δ είναι ένα αδιάστατο μέτρο της ροπής αδράνειας ενός συνδέσμου όπως ορίζεται στην εξίσωση (13).

Αλυσίδα	λ(g/m)	D(cm)	L(cm)	S(cm)	δ
Μικρής μπάλας	16,5	0,30	0,44	0	1,34
Μεγάλης μπάλας	34,0	0,44	0,63	0	1,33
Ράβδου	22,9	0,30	1,02	0,30	0,65

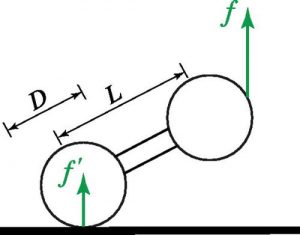
Eik. 3. Σχηματικό διάγραμμα που δείχνει έναν σύνδεσμο της αλυσίδας που ανυψώνεται από το δοχείο, με τις δυνάμεις που επενεργούν σε αυτό και τον τρόπο με τον οποίο επισημαίνονται τα μήκη.

Για να παρατηρηθεί ο πίδακας αλυσίδας, μια αλυσίδα τοποθετήθηκε σε ένα διαφανές, πλαστικό δοχείο που έχει βάση 9 cm × 9 cm και ύψος 13 cm (το δοχείο φαίνεται στην Εικ. 1). Η αλυσίδα αφέθηκε να πέσει σε κουτί από χαρτόνι που είχε στον πάτο μια πάνινη πετσέτα. Για κάθε τύπο αλυσίδας παρατηρήθηκε ο πίδακας για τρία διαφορετικά (κατά μέσον όρο) ύψη πτώσης, τα οποία ορίζονται ως η (μέση) απόσταση από την κορυφή της αλυσίδας στο πάτωμα: 1,29 m, 2,35 m και 3,57 m. Πραγματοποιήθηκαν τουλάχιστον τέσσερις επαναλήψεις σε κάθε ύψος πτώσης.

Το ύψος της αλυσίδας επάνω από το δοχείο προσδιορίστηκε από εγγραφή βίντεο χρησιμοποιώντας το ελεύθερα διαθέσιμο πρόγραμμα ανάλυσης – βίντεο Tracker. Από κάθε βίντεο μιας επανάληψης έγιναν μετρήσεις των υψών h_above ( h_πάνω ) και h_below (h_κάτω). Εδώ, ως h_above ορίζεται η απόσταση σταθερής κατάστασης στην οποία η αλυσίδα ανέρχεται πάνω από την κορυφή του δοχείου που περιέχει το σωρό της αλυσίδας. Προκειμένου να θεωρηθεί ότι βρίσκεται σε σταθερή κατάσταση, απαιτείται η τιμή του h_above να είναι ίδια για πολλά πλαίσια λήψης του βίντεο. Για κάθε βίντεο καταγράφηκαν από μία έως πέντε διαφορετικές μετρήσεις ύψους. Για να διασφαλιστεί ότι οι μετρήσεις αυτές ήταν σχετικά ανεξάρτητες, απαιτείτο να διαχωρίζονται εγκαίρως. Έτσι, ένας μικρότερος αριθμός δεδομένων σημείων ανά βίντεο καταγράφηκε για τις μεγαλύτερες τιμές του h_below επειδή η αλυσίδα κινείται γρηγορότερα και έτσι το πείραμα διήρκεσε μικρότερο χρόνο. Επίσης, το ίδιο συνέβη για την αλυσίδα μικρών σφαιρών επειδή τείνει να μπερδεύεται πιο συχνά. Από τις μετρούμενες τιμές του h_above και του h_below υπολογίστηκε ο αδιάστατος λόγος h_above / h_below . Η μέση και τυπική απόκλιση αυτής της αναλογίας είναι η γραφική παράσταση στην Εικ. 4.

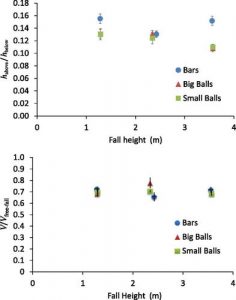
Εικ. 4. Οι μετρούμενοι (χωρίς διάσταση) λόγοι ως συνάρτηση του ύψους πτώσης h_below καθορίζονται για τις τρεις διαφορετικές αλυσίδες. Η άνω γραφική παράσταση δείχνει το λόγο του ύψους ανύψωσης προς το ύψος πτώσης (h_above / h_below ) και το κάτω γράφημα δείχνει το λόγο της ταχύτητας αλυσίδας σε σταθερή κατάσταση προς την ταχύτητα ελεύθερης πτώσης (V / V_free-fall). Σημειώστε ότι (i) οι αδιάστατες αναλογίες είναι περίπου σταθερές, ανεξάρτητα από το ύψος πτώσης, και (ii) η αλυσίδα ράβδου ανεβαίνει ελαφρώς υψηλότερα από τις άλλες αλυσίδες.

Επίσης φαίνεται στην Εικ. 4 ο λόγος της ταχύτητας αλυσίδας σταθερής κατάστασης V προς την ταχύτητα ελεύθερης πτώσης V_free-fall.

(1) $\begin{equation*} V_{free-fall}=\sqrt{2gh_{below}} \end{equation*}$

(Η ταχύτητα ελεύθερης πτώσης είναι η τυπική ταχύτητα σταθερής κατάστασης για μία ροή). Για να μετρηθεί η ταχύτητα σταθερής κατάστασης V της αλυσίδας, το χαρτονένιο κουτί που έπληξε η αλυσίδα τοποθετήθηκε σε μια Πλατφόρμα Δύναμης PASCO. Η δύναμη που ασκήθηκε στην πλατφόρμα – το (ενεργό) βάρος W_box του κουτιού – καταγράφηκε ενώ η αλυσίδα πέφτει και ο μέσος ρυθμός μεταβολής αυτής της δύναμης, $\frac{dW_{box}}{dt}$ , προσδιορίστηκε κατά την κίνηση σταθερής κατάστασης. Η ταχύτητα σταθερής κατάστασης της αλυσίδας που πέφτει υπολογίστηκε από τη σχέση

(2) $\begin{equation*} \frac{dW_{box}}{dt}=\lambda g V \end{equation*}$

Όπου λ είναι η μάζα ανά μονάδα μήκους της αλυσίδας και g είναι η ένταση του πεδίου βαρύτητας. Το βάρος W_box θα έχει γενικά μια δυναμική συνεισφορά ανάλογη του λV² . Ωστόσο, αυτό δεν θα συμβάλει στη μέτρηση από την εξίσωση (2).

Γενικά, τα δεδομένα στην Εικ. 4 δείχνουν ότι οι αδιάστατοι λόγοι h_above / h_below και V / V_free-fall είναι ανεξάρτητοι από το ύψος πτώσης. Οι μέσες μετρούμενες τιμές αυτών των λόγων, για κάθε τύπο αλυσίδας, δίδονται στον πίνακα II. Αυτά τα αποτελέσματα συμφωνούν με τη θεωρητικά υπολογισμένη τιμή h_above / h_below= 0.14, για μια αλυσίδα με διαστάσεις παρόμοιες με την αλυσίδα μεγάλης σφαίρας που χρησιμοποιείται εδώ, και παρόμια με αυτά όταν h_below <3,5 m.

Πίνακας II. Μετρούμενες και προβλεπόμενες παρατηρήσεις για τον πίδακα αλυσίδας. Οι μετρούμενες τιμές είναι οι μέσοι όροι των αδιάστατων λόγων που απεικονίζονται στην Εικ. 4. Όλες οι αβεβαιότητες είναι μόνο στατιστικές. Οι προβλεπόμενες τιμές του h_above / h_below, V / V_{free-fall. πτώσης} και θ_c υπολογίζονται χρησιμοποιώντας τις Εξισ. (19), (7) και (18) αντίστοιχα.

	Πειραματικά μετρούμενες τιμές		Θεωρητικά προβλεπόμενες τιμές
	h_πάνω/h_κάτω	V/V_{ελεύθ. πτώσης}	h_πάνω/h_κάτω	V/V_{ελεύθ. πτώσης}
Μικρής μπάλας	$0,12 \pm 0,01$	$0,70 \pm 0,03$	0,13	0,74
Μεγάλης μπάλας	$0,12 \pm 0,01$	$0,69 \pm 0,03$	0,13	0,74
Ράβδου	$0,14 \pm 0,01$	$0,71 \pm 0,04$	0,32	0,75

III. ΘΕΩΡΗΤΙΚΕΣ ΕΠΕΞΗΓΗΣΕΙΣ

Α. Δυνάμεις στoν πίδακα αλυσίδας

Ένα σκίτσο των δυνάμεων σταθερής κατάστασης που δρουν στον πίδακα αλυσίδας φαίνεται στην Εικ. 5. Για λόγους υπολογισμού, η αλυσίδα έχει διασπαστεί στα τρία τμήματα: το (μικρό) τμήμα στο σωρό που ανασηκώνεται από το δοχείο, το τμήμα πάνω από την κορυφή του σωρού και το τμήμα κάτω από το σωρό. Έχουν σχεδιαστεί οι δυνάμεις σταθερής κατάστασης που δρουν σε κάθε τμήμα της αλυσίδας στο σκίτσο. Οι δυνάμεις που επενεργούν στο τμήμα της αλυσίδας που ανασηκώνεται έξω από το δοχείο παρουσιάζονται στην αριστερή πλευρά του σκίτσου (πράσινο), εκείνες που δρουν στο τμήμα πάνω από το σωρό εμφανίζονται στη μέση (μπλε) και εκείνες που δρουν στο τμήμα κάτω από το σωρό εμφανίζονται στα δεξιά (κόκκινο).

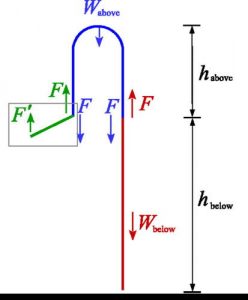
Εικ. 5. Διάγραμμα των δυνάμεων που επενεργούν στον πίδακα αλυσίδας.

Για το τμήμα κάτω από το σωρό υπάρχουν δύο δυνάμεις που έχουν σχεδιαστεί: το βάρος W_below (W_κάτω) του τμήματος αυτού της αλυσίδας και η τάση F στην αλυσίδα στην κορυφή του τμήματος. Οποιαδήποτε δύναμη ενεργεί στο κάτω άκρο της αλυσίδας, που προσκρούει στο έδαφος, έχει παραληφθεί. Αυτή η προσέγγιση είναι δικαιολογημένη επειδή η αλυσίδα δεν θα υποστηρίξει μια προς τα άνω (συμπιεστική) δύναμη και οποιαδήποτε δύναμη προς τα κάτω (τάση), όπως παρατηρήθηκε σε μερικά πειράματα, είναι μικρή και δεν είναι κρίσιμη για την κατανόηση του φαινομένου του πίδακα. Επειδή αυτό το τμήμα της αλυσίδας δεν επιταχύνεται (σε σταθερή κατάσταση), οι δυνάμεις πρέπει να ισορροπήσουν, δίνοντας

(3) $\begin{equation*} F=W_{below} \end{equation*}$

Τα άλλα δύο τμήματα της αλυσίδας επιταχύνονται (αν και η ταχύτητα είναι σταθερή στο άνω τμήμα, η κατεύθυνση της ταχύτητας δεν είναι). Για να περιγράψουμε την κίνηση της αλυσίδας σε αυτές τις περιοχές, θα χρησιμοποιηθεί μια εξειδικευμένη μορφή νόμου του Νεύτωνα κατάλληλη για ένα σταθερό όγκο ενός συστήματος συνεχούς μάζας. Αθροίζοντας $\vec{f_{o \lambda}}=m \vec{a}$ στην αλυσίδα σε μια σταθερή περιοχή και υποθέτοντας ότι το σύστημα βρίσκεται σε σταθερή κατάσταση παίρνουμε

(4) $\begin{equation*} \vec{f_{o \lambda}}=Q \Delta \vec{\nu} \end{equation*}$

Όπου $\vec{f_{o \lambda}}$ είναι η συνισταμένη δύναμη στην περιοχή, το Q είναι ο ρυθμός ροής μάζας μέσα από τα όρια της περιοχής και το $\Delta \vec{\nu}$ είναι η μεταβολή της ταχύτητας της αλυσίδας μεταξύ των ορίων. Η εξίσωση (4) είναι η εφαρμογή στη σταθερή κατάσταση αυτού που είναι κοινώς γνωστό ως αρχή διατήρησης ορμής ή θεώρημα ορμής. Επειδή το σύστημα βρίσκεται σε σταθερή κατάσταση, η ολική ορμή σε μια σταθερή περιοχή δεν αλλάζει. Έτσι, η συνισταμένη δύναμη που ασκείται στην περιοχή είναι ίση με τη ροή της ορμής έξω από την περιοχή. Ο ρυθμός ροής της ορμής μέσω ενός συνόρου περιγράφεται ποσοτικά από την ταχύτητα $\vec{\nu}$ επί το ρυθμό ροής μάζας μέσω του συνόρου, $Q = \lambda \nu$ , όπου λ είναι η γραμμική πυκνότητα μάζας της αλυσίδας.

Για το τμήμα της αλυσίδας πάνω από το σωρό υπάρχουν τρεις δυνάμεις που δρουν (βλέπε Εικ. 5): το βάρος W_above (W_πάνω) αυτού του τμήματος της αλυσίδας και, στο κάτω όριο, οι δύο δυνάμεις εφελκυσμού στα άκρα της αλυσίδας. Επειδή η αλυσίδα είναι σε σταθερή κατάσταση κίνησης, αυτές οι δύο δυνάμεις εφελκυσμού πρέπει να έχουν την ίδια τιμή, F. Εφαρμόζοντας την εξίσωση (4) στην περιοχή αυτή οδηγεί στο

(5) $\begin{equation*} 2F+W_{above}=2 \lambda V^2 \end{equation*}$

Η αριστερή πλευρά της εξ. (5) είναι η συνολική προς τα κάτω δύναμη της αλυσίδας σε αυτή την περιοχή και η δεξιά πλευρά είναι η προς τα κάτω μεταβολή της ροής ορμής: $\lambda V^2$ κατεβαίνοντας, μείον $\lambda V^2$ ανεβαίνοντας (και ως εκ τούτου αντίθετο πρόσημο).
Για το τμήμα της αλυσίδας στο δοχείο, επικεντρωνόμαστε στους λίγους δεσμούς αλυσίδας στην μεταβατική περιοχή, όπου μεταβάλλονται από οριζόντιοι και ακίνητοι σε κάθετοι και κινούμενοι προς τα πάνω. Η δύναμη F τραβά αυτό το τμήμα της αλυσίδας προς τα πάνω στο άνω όριο της περιοχής και το δοχείο παρέχει μια επιπλέον προς τα πάνω δύναμη $F'$ στην αλυσίδα στο κατώτερο όριο αυτής της περιοχής (βλέπε Εικ. 5). Οποιεσδήποτε οριζόντιες δυνάμεις που δρουν σε αυτό το τμήμα της αλυσίδας έχουν αγνοηθεί. Η παράβλεψη των οριζόντιων δυνάμεων εδώ πρέπει να είναι εύλογη επειδή η αλυσίδα είναι σχετικά χωρίς περιορισμούς στην οριζόντια κατεύθυνση και επειδή δεν υπάρχει καθαρός προσανατολισμός των συνδέσμων των αλυσίδων, έτσι ώστε τα αποτελέσματα των οριζόντιων δυνάμεων να τείνουν να ακυρώνονται. Εφαρμόζοντας την εξίσωση (4) στην περιοχή αυτή παίρνουμε

(6) $\begin{equation*} F+F' = \lambda V^2 \end{equation*}$

Όπου $F'$ είναι η μέση δύναμη που ενεργεί προς τα πάνω στον πυθμένα της περιοχής αυτής, το F είναι η μέση δύναμη που ενεργεί προς τα πάνω στην κορυφή της περιοχής και $\lambda V^2$ είναι η ροή της ορμής προς τα πάνω και προς τα έξω αυτής της περιοχής. Η βαρυτική δύναμη που ασκείται σε αυτή την περιοχή παραλείπεται επειδή αυτό το τμήμα περιέχει μόνο λίγους συνδέσμους, έτσι το βάρος τους θα είναι μικρό σε σύγκριση με τις άλλες δυνάμεις στην εξίσωση (6).

Ο αδιάστατος λόγος της ταχύτητας της αλυσίδας σταθερής κατάστασης προς την ταχύτητα ελεύθερης πτώσης, $V_{free-fall}$ , μπορεί να υπολογιστεί συνδυάζοντας τις εξισώσεις (1), (3) και (5) για να δώσει

(7) $\begin{equation*} \frac{V}{V_{free-fall}}=\sqrt{\frac{1}{2} \left ( 1+\frac{W_{above}}{2W_{below}}\right )} \approx \sqrt{\frac{1}{2} \left ( 1+\frac{h_{above}}{h_{below}}\right )} \end{equation*}$

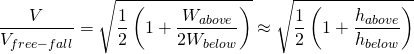
Το τελευταίο μέρος της Εξ. (7) κάνει χρήση του γεγονότος ότι $W_{below} \approx \lambda h_{below} g$ και $W_{above} \approx \lambda 2h_{above} g$ , όπου η καμπύλη στο επάνω τμήμα έχει παραμεληθεί. Σημειώστε ότι η Εξ. (7) συσχετίζει τις δύο παρατηρήσεις που απεικονίζονται στην Εικ. 4 και έτσι δίνει ένα έλεγχο συνέπειας στο μοντέλο. Επίσης, η εξαγωγή της Εξ. (7) δεν έκανε χρήση της Εξ. (6), οπότε είναι ανεξάρτητη από το πώς αλληλεπιδρούν οι σύνδεσμοι με το δοχείο.

Οι τιμές του λόγου $V / V_{free-fall}$ που προβλέπονται στην εξίσωση (7), και όπως υπολογίζεται από τις παρατηρούμενες τιμές του $h_{above} / h_{below}$ , δίδονται στον Πίνακα II. Οι προβλεπόμενες τιμές είναι ελαφρώς μεγαλύτερες, αλλά γενικά σε λογική συμφωνία, με τις μετρούμενες τιμές. Σημειώστε ότι η μικρή συστηματική απόκλιση είναι πολύ μεγάλη για να εξηγηθεί από την προσέγγιση της παραμέλησης της καμπυλότητας στην κορυφή της αλυσίδας. Επιπλέον, πρέπει να επισημανθεί ότι η προσθήκη πτωτικής δύναμης στο κάτω μέρος της αλυσίδας θα καθιστούσε χειρότερη αυτή τη μικρή απόκλιση. Η ασυμφωνία μπορεί να οφείλεται σε δύναμη αντίστασης που ασκείται στην κινούμενη αλυσίδα.

Ο (αδιάστατος) λόγος του ύψους ανύψωσης προς το ύψος πτώσης μπορεί να υπολογιστεί συνδυάζοντας τις εξισώσεις (3), (5) και (6) για να δώσει

(8) $\begin{equation*} \frac{F}{F'}=\frac{W_{above}}{2W_{below}} \approx \frac{h_{above}}{h_{below}}} \end{equation*}$

Όπου το καμπύλο τμήμα στην κορυφή της αλυσίδας δε λήφθηκε υπόψη και πάλι. Η εξίσωση (8) δείχνει ότι η αλυσίδα ανυψώνεται πάνω από το σωρό απευθείας λόγω της δύναμης αντίδρασης $F'$ . Για τον υπολογισμό του $F'$ απαιτείται ένα μοντέλο για την αλληλεπίδραση μεταξύ ενός συνδέσμου και του δαπέδου του δοχείου προκειμένου να προσδιοριστεί πώς μια προς τα πάνω έλξη δύναμης μέσης τιμής F στο ένα άκρο του συνδέσμου, παράγει μια προς τα άνω δύναμη μέσης τιμής $F'$ στο άλλο άκρο.

Το μοντέλο της κίνησης της αλυσίδας που παρουσιάζεται εδώ δεν προϋποθέτει ρητά ότι η μηχανική ενέργεια της αλυσίδας διατηρείται. Η διατήρηση της μηχανικής ενέργειας στις πτώσεις των αλυσίδων υπήρξε θέμα συζήτησης και σύγχυσης στη βιβλιογραφία. Η τρέχουσα συναίνεση είναι ότι οι θεωρητικοί υπολογισμοί που υποθέτουν τη διατήρηση της μηχανικής ενέργειας περιγράφουν με ακρίβεια αλυσίδες που ξεδιπλώνονται ομαλά, αλλά αποτυγχάνουν στην περιγραφή αλυσίδων που κινούνται μέσα ή έξω από ένα σωρό. Μια αφελής εφαρμογή διατήρησης ενέργειας στον πίδακα αλυσίδας θα προέβλεπε ότι η ταχύτητα σταθερής κατάστασης της αλυσίδας πρέπει να είναι η ταχύτητα ελεύθερης πτώσης $V_{free-fall}$ , το βασικό αποτέλεσμα για μία ροή. Ωστόσο, η Εξ. (7) προβλέπει ότι $V / V_{free-fall}<1$ , δεδομένου ότι είναι και $h_{above} / h_{below}<1$ . Ο λόγος για τη διαφορά μπορεί να εντοπιστεί πίσω από αυτό που συμβαίνει όταν ένας δεσμός ανυψώνεται από το σωρό στο δοχείο. Το συνολικό έργο που γίνεται στο σύνδεσμο καθώς περιστρέφεται από οριζόντια θέση σε κάθετη είναι $E_{total} = FL$ , η ανυψωτική δύναμη F επί την απόσταση L που αυτή η δύναμη δρα (βλέπε Εικ. 3, L είναι το μήκος της ζεύξης ενώ το πάχος του συνδέσμου έχει παραμεληθεί για λόγους απλοποίησης). Σημειώστε ότι η δύναμη αντίδρασης $F'$ δεν δουλεύει πάνω στο σύνδεσμο επειδή το άκρο του συνδέσμου σε επαφή με το δοχείο δεν κινείται κατακόρυφα. To συνολικό έργο μπορεί να χωριστεί σε δύο μέρη, $E_{total} = E_{trans} + E_{rot}$ , τα ποσά που πηγαίνουν στην αύξηση της μεταφορικής, ( $E_{trans}$ ), και περιστροφικής ( $E_{rot}$ ) κινητικής ενέργειας του συνδέσμου. To μεταφορικό έργο ισούται με τη συνολική μέση δύναμη που επενεργεί επί του συνδέσμου επί την απόσταση που μετακινείται το κέντρο της μάζας του συνδέσμου καθώς στρέφεται από την οριζόντια σε κατακόρυφη θέση, $E_{trans} = (F + F ') (L / 2)$ . Εξισώνοντας αυτό με τη μεταβολή της κινητικής ενέργειας μεταφοράς, $1/2MV^2$ (όπου M είναι η μάζα του συνδέσμου), και χρησιμοποιώντας λ = M / L, παίρνουμε την Εξ. (6). Επομένως, είναι το μεταφορικό έργο αυτό που προκαλεί τη μαζική κίνηση της αλυσίδας. Η περιστροφικό έργο προκύπτει με το ολοκλήρωμα της συνολικής ροπής στο σύνδεσμο κατά τη στροφή από την οριζόντια θέση στην κάθετη, δίνοντας $E_{rot} = (F - F ') (L / 2)$ , το οποίο συμφωνεί με τη διαφορά $E_{total} - E_{trans}$ . Αυτό το περιστροφικό έργο δημιουργεί μια περιστροφική κινητική ενέργεια του συνδέσμου και συνεπώς αποκλίσεις της αλυσίδας από γραμμική / ομαλή κίνηση. Αυτή η τελευταία μηχανική ενέργεια δεν συμβάλλει στη μαζική κίνηση της αλυσίδας αλλά αντ’ αυτού μεταφέρεται κατά μήκος της αλυσίδας ως κύμα. Έτσι, τα αποτελέσματα εδώ συμφωνούν με την τυπική συμφωνία στη βιβλιογραφία για τη διατήρηση ενέργειας στις αλυσίδες.

Είναι ενδιαφέρον να σημειωθεί ότι η Εξ. (5) μπορεί να εφαρμοστεί κοντά στην κορυφή της αλυσίδας (όπου $W_{above} \approx 0$ ) για να πάρουμε $T \approx \lambda V^2$ , όπου Τ είναι η τάση στην κορυφή. Αυτό το αποτέλεσμα για μια περιστρεφόμενη αλυσίδα ή χορδή μπορεί να βρεθεί σε πολλά εγχειρίδια και έχει σχέση με τις συζητήσεις για την επίδειξη μέσα στην τάξη ενός βρόχου περιστρεφόμενης αλυσίδας που κυλίεται κατά μήκος του δαπέδου.

Β. Λεπτομερές μοντέλο της αλληλεπίδρασης συνδέσμου-δοχείου

Η κίνηση του συνδέσμου που έρχεται σε επαφή με το πάτωμα του δοχείου (ή το σωρό) καθορίζεται από τις δυνάμεις και τις ροπές που επενεργούν σε αυτό. Εδώ, ένας σύνδεσμος ορίζεται ως δύο (κοίλες) σφαίρες συνδεδεμένες με μία ράβδο, όπως φαίνεται σττην Εικ. 3. Η εφαρμογή του δεύτερου νόμου του Νεύτωνα στην κίνηση του κέντρου της μάζας του συνδέσμου δίνει

(9) $\begin{equation*} f+f'= M \frac{d \nu}{dt} \end{equation*}$

Όπου M είναι η μάζα του συνδέσμου, v είναι η (κάθετη) ταχύτητα του κέντρου της μάζας και τα σύμβολα μικρά γράμματα χρησιμοποιούνται τώρα για να αντιπροσωπεύουν τις εξαρτώμενες από το χρόνο εκδόσεις των ανάλογων ποσοτήτων στο Κεφ. ΙΙΙ Α (Οι δυνάμεις $F$ και $F '$ είναι οι μέσες χρονικά τιμές, $F=\langle f \rangle$ και $F'=\langle f \rangle$ και η ταχύτητα σταθερής κατάστασης V είναι η τελική ταχύτητα του κέντρου μάζας του συνδέσμου, $V = V_{final}$ .) Για την περιστροφή του συνδέσμου ως προς το κέντρο της μάζας η εξίσωση της κίνησης είναι

(10) $\begin{equation*} \bigg [ f \bigg ( \frac{L+D}{2} \bigg ) - f' \bigg (\frac{L}{2} \bigg ) \bigg ] cos \theta =I_{cm} \frac{d \omega}{dt} \end{equation*}$

Όπου θ είναι η γωνία μεταξύ του συνδέσμου και της οριζόντιας διεύθυνσης, ω = dθ / dt είναι η γωνιακή ταχύτητα του συνδέσμου γύρω από το κέντρο της μάζας και $I_{cm}$ είναι η ροπή αδράνειας γύρω από το κέντρο της μάζας (βλ. Εικ. 3),

Θα πρέπει να σημειωθεί ότι η Εξ. (10) υποθέτει ότι ο σύνδεσμος είναι μια άκαμπτη δομή, οπότε η εφαρμογή της σε μια αλυσίδα μπάλας είναι προσεγγιστική. Επίσης, σημειώστε ότι για μια αλυσίδα μπάλας οι δύο σφαίρες που αποτελούν το σύνδεσμο αλλάζουν σε όλη τη διαδικασία. Καθώς μία σφαίρα φεύγει από την οριζόντια επιφάνεια, αυτή η σφαίρα και η γειτονική σφαίρα που βρίσκεται ακόμα σε επαφή με την επιφάνεια, αποτελούν μία σύνδεση. Μετά από ένα σύντομο χρονικό διάστημα, η κάτω σφαίρα αυτής της ζεύξης θα αφήσει την επιφάνεια, οπότε θα γίνει η ανώτερη σφαίρα του επόμενου συνδέσμου.

Οι γραμμικές και περιστροφικές κινήσεις του συνδέσμου, όπως περιγράφονται στις εξισώσεις (9)και (10), δεν είναι ανεξάρτητες επειδή ο σύνδεσμος είναι σε επαφή με το πάτωμα του δοχείου (ή το σωρό). Όσο ο σύνδεσμος παραμένει σε επαφή με το δάπεδο, η κατακόρυφη ταχύτητα της κάτω σφαίρας θα είναι μηδενική, δηλαδή

(11) $\begin{equation*} \nu_{bottom}=\nu- \omega \frac{L}{2} cos \theta =0 \end{equation*}$

Συνδυάζοντας τις εξισώσεις (9)-(11) και λύνοντας ως προς $f'$ για τυχαία γωνία θ και γωνιακή ταχύτητα ω, παίρνουμε

(12) $\begin{equation*} f'= \bigg (\frac{1+D/L-\delta}{1+\delta} \bigg )f-\frac{(2+D/L) \delta sin^2 \theta}{(cos^2 \theta+ \delta)(1+\delta)}f- \frac{\delta ML \omega^2 sin \theta}{2(cos^2 \theta+ \delta)} \end{equation*}$

όπου

(13) $\begin{equation*} \delta =\frac{4I_{cm}}{ML^2} \end{equation*}$

είναι ένα (αδιάστατο) μέτρο της ροπής αδράνειας γύρω από το κέντρο της μάζας.

Η εξίσωση (12) έχει γραφτεί σε μια μορφή όπου ο πρώτος όρος είναι η αρχική δύναμη αντίδρασης, f ‘(θ = 0), ενώ ο δεύτερος και ο τρίτος όρος περιγράφουν τη μεταβολή της δύναμης αντίδρασης καθώς ο σύνδεσμος περιστρέφεται προς τα πάνω. Αυτοί οι “διορθωτικοί όροι” μπορούν να γίνουν κατανοητοί. Ο δεύτερος όρος προκύπτει από τη μείωση του κάθετου βραχίονα, ο οποίος μειώνει τη ροπή από το f και επομένως το μέγεθος της δύναμης αντίδρασης $f'$ . Ο τρίτος όρος προκύπτει από τη γωνιακή κίνηση, η οποία προκαλεί μια επιτάχυνση που μοιάζει με κεντρομόλο προς τα κάτω, η οποία προκαλεί τη μείωση της συνολικής προς τα πάνω επιτάχυνσης και έτσι η δύναμη προς τα πάνω του συνδέσμου από το δοχείο πρέπει επίσης να μειωθεί.

Η αδιάστατη παράμετρος δ εξαρτάται από το σχήμα του συνδέσμου. Για τη διαμόρφωση σύνδεσης που φαίνεται στην Εικ. 3 και αγνοώντας τη μάζα των συνδετικών ράβδων σε σύγκριση με τη μάζα των (κοίλων) σφαιρών, ο υπολογισμός της ροπής αδράνειας δίνει την παράμετρο δ περίπου

(14) $\begin{equation*} \delta \approx 1+\frac{2}{3} \bigg ( \frac{D}{L} \bigg )^2 \end{equation*}$

Για την αλυσίδα ράβδου, επιλέγεται ο σύνδεσμος έτσι ώστε να είναι η απλούστερη δυνατή γενίκευση της Εικ. 3, όπου κάθε μπάλα αντικαθίσταται απλά από μία ράβδο. Κάθε ράβδος υποτίθεται ότι είναι δύο (κοίλα) ημισφαίρια συνδεδεμένα με έναν κύλινδρο. Ο υπολογισμός της ροπής αδράνειας δίνει στη συνέχεια την παράμετρο δ ως

(15) $\begin{equation*} \delta \approx \bigg (1-\frac{S}{L} \bigg )^2 + \frac{M_s}{M} \bigg [\frac{2}{3} \bigg ( \frac{D}{L} \bigg )^2 +\bigg ( \frac{S}{L} \bigg ) \bigg ( \frac{D}{L} \bigg )+\bigg ( \frac{S}{L} \bigg )^2 \bigg ]+\frac{M_c}{M} \bigg [\frac{1}{2} \bigg ( \frac{D}{L} \bigg )^2 +\frac{1}{3}\bigg ( \frac{S}{L} \bigg )^2 \bigg ] \end{equation*}$

Όπου $M_S$ είναι η ολική μάζα στα δύο ημισφαίρια, $M_C$ είναι η συνολική μάζα στο κυλινδρικό τμήμα, ενώ η μάζα στη συνδετική μπάρα έχει και πάλι αγνοηθεί (έτσι ώστε $M = M_S + M_C$ ). Θεωρώντας την πυκνότητα και το πάχος του μετάλλου στους συνδέσμους ίδια παντού, αυτές οι ποσότητες ακυρώνονται στους λόγους των μαζών, έτσι ώστε να μπορεί κανείς να πάρει $M_S \propto \pi D^2$ και $M_C \propto \pi DS$ . Για τις αλυσίδες που χρησιμοποιούνται εδώ οι τιμές δ που δίδονται στις εξισώσεις (14) και (15) παρατίθενται στον Πίνακα Ι.

Αρχικά, ο σύνδεσμος είναι οριζόντιος (θ = 0) και σε ηρεμία (ω = 0) και ο δεύτερος και τρίτος όρος στην εξίσωση (12) εξαφανίζονται. Στην περίπτωση αυτή το $f'$ είναι ένας μικρός, θετικός αριθμός, όπως αναμένεται από τις παρατηρήσεις. Καθώς ο σύνδεσμος περιστρέφεται προς τα πάνω και τα θ και ω γίνονται μη μηδενικά, ο δεύτερος και ο τρίτος όρος στην Εξ. (12) προκαλούν μείωση του $f'$ . Πριν το θ πάρει την τιμή π / 2 υπάρχει μια κρίσιμη γωνία $\theta_c$ όπου $f'= 0$ . Για γωνίες (πολλαπλάσιες) πέρα από αυτό το κρίσιμο σημείο, ο σύνδεσμος αφήσει τον πάτο του δοχείου και η εξίσωση περιορισμού (11) στο κάτω άκρο του συνδέσμου δεν ισχύει πλέον. Ως αποτέλεσμα, επίσης και η Εξ. (12) δεν ισχύει πλέον. Μόλις ο σύνδεσμος ανυψωθεί από το πάτωμα του δοχείου, γίνεται τμήμα της αλυσίδας που τροφοδοτεί την προς τα πάνω δύναμη f στον επόμενο σύνδεσμο που έχει ακόμα ένα άκρο στο πάτωμα του δοχείου.

Για να βρείτε το λόγο του ύψους ανύψωσης προς το ύψος πτώσης, όπως αναφέρεται στην εξίσωση (8), ο μέσος όρος της $f'$ είναι απαραίτητος κατά τη στιγμή που ο κρίκος είναι σε επαφή με το πάτωμα. Αυτός ο μέσος όρος θα ήταν δύσκολο να προσδιοριστεί επακριβώς, αλλά δεν είναι δύσκολο να υπολογιστεί στο περίπου. Η προσέγγιση που γίνεται είναι ότι η συμβολή του δεύτερου και του τρίτου όρου στην εξίσωση (12) είναι μικρή σε σύγκριση με τον πρώτο όρο και ότι μπορούν να αντιμετωπίζονται ως διακυμάνσεις. Αυτή η προσέγγιση είναι εύλογη επειδή η βάβδος κινείται πιο αργά στην αρχική χρονική στιγμή όπου θ = 0 και επομένως ο πρώτος όρος θα συμβάλει περισσότερο στο χρονικό μέσο χρόνο.

Παραλείποντας το δεύτερο και τρίτο όρο στην Εξ. (12), και υποθέτοντας ότι η f είναι σταθερή στο χρόνο (έτσι ώστε f = F), η Εξ.(10) μπορεί να λυθεί ακριβώς για να δώσει

(16) $\begin{equation*} \omega^2 \approx \bigg (\frac{4F}{ML} \bigg ) \bigg (\frac{2+D/L}{1+\delta} \bigg ) sin \theta \end{equation*}$

Η υπόθεση ότι η f είναι σταθερή μπορεί να φαίνεται δραστική, ωστόσο, η εξάρτηση της f από το χρόνο επηρεάζει μόνο τους διακυμαντικούς όρους διόρθωσης και επομένως μπορεί να θεωρηθεί ως διόρθωση υψηλότερης τάξης που είναι αμελητέα στο πρώτο επίπεδο διόρθωσης. Αντικαθιστώντας αυτή την έκφραση για το $\omega^2$ στην Εξ. (12) οδηγούματσε στη συνέχεια

(17) $\begin{equation*} \frac{f'}{F} \approx \frac{1+D/L- \delta}{1+\delta}-\frac{3(2+D/L) \delta sin^2 \theta}{(cos^2 \theta+ \delta)(1+\delta)} \end{equation*}$

Αυτή η εξίσωση εύκλολα τώρα μπορεί να λυθεί ως προς την κρίσιμη γωνία, θέτoντας $f'=0$ , οπότε παίρνουμε

(18) $\begin{equation*} sin^2 \theta \approx \frac{(1+D/L-\delta)(1+\delta)}{1+D/L+\delta(5+3D/L)} \end{equation*}$

Η κρίσιμη γωνία (η γωνία που σχηματίζει ο σύνδεσμος με το δάπεδο του δοχείου όταν αρχίζει να απομακρύνεται από το δάπεδο) είναι μια παρατηρήσιμη ποσότητα. Σημειώστε ότι η κρίσιμη γωνία είναι ανεξάρτητη από το ύψος πτώσης $h_{below}$ και την πυκνότητα μάζας λ και εξαρτάται μόνο από τον τρόπο κατανομής της μάζας στους κρίκους της αλυσίδας μέσω των παραμέτρων D / L και δ.

Οι κρίσιμες γωνίες για τις αλυσίδες που χρησιμοποιούνται εδώ, όπως υπολογίστηκαν χρησιμοποιώντας την εξίσωση (18), δίδονται στον Πίνακα II. Αυτές οι γωνίες είναι μάλλον μικρές, οι οποίες έχουν δύο σημαντικές επιπτώσεις. Πρώτον, σημειώστε ότι αυτές οι γωνίες είναι μικρότερες από το μέτρο της κάμψης που είναι δυνατή στη διασταύρωση μεταξύ μίας σφαίρας και μιας ράβδου σύνδεσης. Αυτό το γεγονός δικαιολογεί την επιλογή ενός συνδέσμου αποτελούμενου από τη μικρότερη δυνατή μονάδα, δύο μπάλες. Δεύτερον, είναι σκόπιμο να χρησιμοποιείται η προσέγγιση μικρών γωνιών κατά τον υπολογισμό του μέσου χρόνου στην εξίσωση (17).

Στην κατώτατης τάξης προσέγγιση μικρής γωνίας παίρνουμε $cos^2 \theta \approx 1$ και $sin^2 \theta \approx \theta^2$
στην εξίσωση (17) και σημειώστε, από την εξίσωση (16), ότι η γωνιακή επιτάχυνση είναι πλέον σταθερή στο χρονικό διάστημα. Έτσι, $\theta \propto t^2$ και η χρονική μέση τιμή του $\theta^2$ μειώνεται στο ${\theta_c}^2 / 5$ . Ο λόγος των υψών πάνω και κάτω από το δοχείο, όπως δίδεται στην Εξ. (8) είναι τώρα

(19) $\begin{equation*} \frac{h_{above}}{h_{below}} \approx \bigg (\frac{1+D/L-\delta}{1+\delta} \bigg ) \bigg \{1-\frac{3}{5} \frac{(2+D/L)\delta}{[1+D/L+\delta(5+3D/L)]} \bigg \} \end{equation*}$

Σημειώστε ότι το δεξιό μέλος της εξίσωσης (19) είναι ανεξάρτητη από την $h_{below}$ και λ, σε συμφωνία με τις παρατηρήσεις. Ο διορθωτικός όρος είναι αρνητικός επειδή το $f'$ μειώνεται όσο αυξάνεται το θ, όπως σημειώνεται στην Εξ. (12). Ποσοτικά, για τις τρεις διαφορετικές αλυσίδες που χρησιμοποιούνται, οι διορθωτικοί όροι είναι το πολύ 19% του όρου βασικής τάξης. Αυτό το μικρό μέγεθος καταδεικνύει τη συνέπεια στην προσέγγιση των διακυμάνσεων.

Η μορφή του πρώτου παράγοντα στις παρενθέσεις στην εξίσωση (19) μπορεί να κατανοηθεί ποιοτικά ως εξής. Ο αδιάστατος συντελεστής 1 + δ στον παρονομαστή είναι περίπου ανάλογος της ροπής αδράνειας του συνδέσμου γύρω από το άκρο που έρχεται σε επαφή με το δάπεδο. Όσο μεγαλύτερη είναι αυτή η ροπή αδράνειας, τόσο λιγότερο περιστρέφεται ο σύνδεσμος σε σχέση με την κατακόρυφη κίνηση και τόσο μικρότερη είναι η δύναμη αντίδρασης από το δοχείο. Εν τω μεταξύ, ο συντελεστής 1 + D / L-δ στον αριθμητή καθίσταται μηδέν όταν δ = 1 + D / L, που αντιστοιχεί στο “κέντρο κρούσης” στο τέλος του συνδέσμου όπου εφαρμόζεται η δύναμη f. Το κέντρο κρούσης είναι ένας όρος που χρησιμοποιείται συνήθως όταν περιγράφονται τα ρόπαλα του μπέιζμπολ, οι ρακέτες του τένις ή τα σπαθιά. Όταν εφαρμόζεται δύναμη στο κέντρο της κρούσης, δεν υπάρχει δύναμη αντίδρασης στον άξονα περιστροφής (συνήθως όταν τα χέρια συγκρατούν τη ρόπαλο του μπέιζμπολ, την ρακέτα του τένις ή το ξίφος). Στην παρούσα περίπτωση, με το κέντρο κρούσης στη θέση όπου εφαρμόζεται η f, η δύναμη αντίδρασης $f'= 0$ , η οποία οδηγεί σε μηδενικό ύψος για τον πίδακα αλυσίδας από την εξίσωση (8).

Οι τιμές του $h_{above} / h_{below}$ που προβλέπονται στην εξίσωση (19) από το σχήμα των συνδέσμων δίνονται στον Πίνακα II. Οι μετρούμενες και προβλεπόμενες τιμές στον Πίνακα II για τις δύο αλυσίδες μπάλας συμφωνούν με τις στατιστικές αβεβαιότητες. Η αλυσίδα ράβδου έχει μια πιο ομοιόμορφη κατανομή μάζας από τις αλυσίδες μπάλας, και έτσι προβλέπεται ότι θα έχει μεγαλύτερο $h_{above} / h_{below}$ , σε ποιοτική συμφωνία με τις μετρήσεις. Ωστόσο, για την αλυσίδα ράβδου, η απόκλιση μεταξύ των προβλεπόμενων και των μετρηθεισών τιμών είναι μεγάλη.

IV. ΣΥΖΗΤΗΣΗ

Α. Ποσοτική επιτυχία του μοντέλου για το h_above/h_below

Το μοντέλο που προτείνεται εδώ για τον υπολογισμό του $h_{above} / h_{below}$ δεν έχει ελεύθερες παραμέτρους. Ωστόσο, ενώ δεν υπάρχουν ρυθμιζόμενες παράμετροι, έγιναν πολλές επιλογές ως προς τη δομή του μοντέλου. Εδώ συζητούνται μερικές από αυτές τις επιλογές και οι συνέπειές τους.

Η πρόβλεψη για το λόγο $h_{above} / h_{below}$ επηρεάζεται από το πώς ορίζεται ένας δεσμός. Για παράδειγμα, η αγνόηση του πάχους των συνδέσμων οδηγεί σε δραστικά διαφορετικά αποτελέσματα. Η επιλογή που γίνεται εδώ, που φαίνεται στην Εικ. 3, είναι η πιο φυσική για μια αλυσίδα μπάλας. Αλλά αυτή η επιλογή είναι πολύ πιο προβληματική για μια αλυσίδα ράβδου. Για παράδειγμα, όταν η αλυσίδα είναι σε κατάσταση ηρεμίας στο δοχείο, είναι σχεδόν βέβαιο ότι υπάρχουν κάποιες κάμψεις μεταξύ οποιωνδήποτε δύο γειτονικών ράβδων. Έτσι, η περιστροφή ενός συνδέσμου που αποτελείται από δύο τέτοιες ράβδους σε έναν ευθύ, κατακόρυφο προσανατολισμό δεν θα είναι μια καθαρά επίπεδη διαδικασία (όπως είναι για δύο μπάλες), αλλά θα περιλαμβάνει περιστροφή γύρω από τουλάχιστον δύο διαφορετικούς άξονες. Επιπλέον, για μία αλυσίδα ράβδου το μήκος του βραχίονα της ροπής για τη δύναμη από το δοχείο καθίσταται δυσκολότερο να προσδιοριστεί επειδή αυτή η δύναμη πιθανώς δρα κατά μήκος του ράβδου σε κατάσταση ηρεμίας στο δοχείο και όχι μόνο στο άκρο. Για τους λόγους αυτούς, δεν προκαλεί έκπληξη το γεγονός ότι το μοντέλο που χρησιμοποιείται εδώ για να περιγράψει την αλυσίδα μπάλας δεν λειτουργεί τόσο καλά για την αλυσίδα ράβδου.

Το μοντέλο για την ταχύτητα της αλυσίδας που περιγράφεται στο Κεφ. ΙΙΙ Α υποδηλώνει ότι υπάρχει κάποιος τύπος δύναμης αντίστασης (οπισθέλκουσας). Μια τέτοια δύναμη θα ελαττώσει ελαφρώς τις προβλεπόμενες αναλογίες του $h_{above} / h_{below}$ . Αντίθετα, προσθέτοντας τη μάζα των συνδετικών ράβδων μεταξύ των σφαιρών / ράβδων στον υπολογισμό του δ στις εξισώσεις (14) και (15) θα αυξήσει το M χωρίς να αλλάζει ουσιαστικά το $I_{cm}$ και έτσι θα μειώσει την τιμή του δ, πράγμα που θα αυξήσει ελαφρώς την πρόβλεψη του $h_{above} / h_{below}$ .

Η πρόβλεψη της εξίσωσης (19) είναι ότι ο λόγος $h_{above} / h_{below}$ είναι σταθερός. Αυτό διαφωνεί με παρατηρήσεις ότι το $h_{above} / h_{below}$ μειώνεται σε μεγάλο βαθμό. Οι παρατηρήσεις μπορούν να εξηγηθούν εάν μια πρόσθετη δύναμη, όπως μια δύναμη αντίστασης, είναι σημαντική σε μεγάλο βαθμό. Καθώς η ανάλυση στο Κεφ. ΙΙΙ Α δείχνει ότι η ταυτόχρονη μέτρηση της ταχύτητας σταθερής κατάστασης και περισσότερο του $h_{above} / h_{below}$ θα καθορίσει εάν υπάρχει δύναμη αντίστασης.

Δεδομένης της απλότητας και της έλλειψης ελεύθερων παραμέτρων, το παρόν μοντέλο είναι αρκετά επιτυχημένο.

Β. Πρόσθετες φυσικές επιδράσεις

Υπάρχουν ενδιαφέροντα φυσικά φαινόμενα που δεν σχετίζονται με την πρόβλεψη του $h_{above} / h_{below}$ . Πρώτο από όλα είναι η ταχύτητα των κυμάτων στην αλυσίδα. Τα κύματα παράγονται και στα δύο άκρα της αλυσίδας, σ’ αυτό που φεύγει από το δοχείο και σ’ εκείνο που χτυπά στο πάτωμα. Η ταχύτητα αυτών των κυμάτων δίνεται από τη συνήθη έκφραση για τα κύματα σε χορδή, $\sqrt{T/\lambda}$ , όπου Τ είναι η τάση. Για τον πίδακα αλυσίδας, η τάση είναι μεγαλύτερη στην κορυφή όπου $T \approx \lambda V^2$ . Αντικαθιστώντας αυτή την τάση στον τύπο για την ταχύτητα κύματος προκύπτει ότι η ταχύτητα των κυμάτων είναι ίση με την ταχύτητα της αλυσίδας στην κορυφή της αλυσίδας. Κάτω από την κορυφή, η τάση είναι μικρότερη, ώστε τα κύματα να διαδίδονται πιο αργά από την ταχύτητα της ίδιας της αλυσίδας. Το αποτέλεσμα είναι ότι τα κύματα που δημιουργούνται όταν η αλυσίδα χτυπά στο πάτωμα δεν μπορούν να διαδοθούν στην αλυσίδα. Στο άλλο άκρο της αλυσίδας, τα κύματα που παράγονται στο δοχείο που κινούνται στην ίδια κατεύθυνση με την αλυσίδα κινούνται γρήγορα πάνω από την κορυφή και εξαφανίζονται στο πάτωμα. Εντούτοις, τα κύματα που δημιουργούνται στο δοχείο και διαδίδονται απέναντι από την κίνηση της αλυσίδας αρχικά κινούνται πιο αργά από την αλυσίδα και έτσι μεταφέρονται στην κορυφή της αλυσίδας όπου κολλούν. Αυτό εξηγεί γιατί είναι συνηθισμένο να παρατηρούμε στην κορυφή της αλυσίδας σχετικά παρατεταμένες στρεβλώσεις και όχι μια ομαλή καμπύλη.

Γ. Χρησιμοποιώντας τον πίδακα αλυσίδας για τη διδασκαλία

Υπάρχουν πολλές ευκαιρίες για πρόσθετες εργασίες που αφορούν στον πίδακα αλυσίδας. Όπως ήδη αναφέρθηκε, οι ταυτόχρονες μετρήσεις σταθερών υψών και ταχυτήτων σε μεγάλα $h_{below}$ είναι μία πολύ ενδιαφέρουσα περίπτωση. Μια άλλη δυνατότητα θα ήταν να τεθεί ένας αισθητήρας δύναμης κάτω από το δοχείο για να παρατηρήσουμε άμεσα τη μέση δύναμη αντίδρασης $F'$ μεταξύ της αλυσίδας και του δοχείου. Μία άλλη εργασία θα ήταν η βιντεοσκόπηση του πίδακα αλυσίδας και η μελέτη των κυμάτων που διαδίδονται κατά μήκος της αλυσίδας. Αυτό θα ήταν καλό παράδειγμα για συζητήσεις σχετικά με τις υποκρίσιμες και τις υπερκρίσιμες ροές. Εάν είναι διαθέσιμη μια βιντεοκάμερα υψηλής ταχύτητας, ένα άλλο που θα μπορούσαμε να κάνουμε είναι η παρακολούθηση των αλληλεπιδράσεων μεταξύ της αλυσίδας και του δοχείου. Ένα τέτοιο βίντεο μπορεί να επιτρέψει τη μέτρηση της κρίσιμης γωνίας, η οποία είναι μια νέα παρατήρηση που προβλέπεται από το μοντέλο που παρουσιάζεται εδώ.

Άλλη εργασία θα ήταν η παρατήρηση του πίδακα για μια ευρύτερη ποικιλία αλυσίδων. Οι παρατηρήσεις που αναφέρθηκαν εδώ περιορίζονταν κυρίως στις αλυσίδες τύπου μπάλας, διότι αυτές έχουν χρησιμοποιήσει άλλοι ερευνητές. Το θεωρητικό μοντέλο υποδηλώνει ότι, κατ ‘αρχήν, πολλοί διαφορετικοί τύποι αλυσίδων μπορούν να παράγουν πίδακα. Ωστόσο, οι αλυσίδες τύπου σφαιρών έχουν ένα πλεονέκτημα στο ότι η γωνία κάμψης σε κάθε διασταύρωση είναι περιορισμένη και έτσι οι αλυσίδες αυτές τείνουν να μπερδεύονται λιγότερο στο δοχείο, καθιστώντας ευκολότερη την παρακολούθηση ενός πίδακα.

Όταν κάνουμε μια επίδειξη του πίδακα στην τάξη, καλύπτουμε συνήθως τους βασικούς υπολογισμούς με αυτά που αναφέραμε στο Κεφ. III A και μόνο τον υπολογισμό του όρου κύριας τάξης με την εξίσωση (19). Αυτό διαρκεί περίπου 15 λεπτά και δίνει μια αριθμητική τιμή για σύγκριση με τις μετρήσεις που έγιναν στην επίδειξη. Η αλυσίδα μεγάλης σφαίρας χρησιμοποιείται για αυτές τις επιδείξεις, επειδή μπερδεύεται λιγότερο συχνά από την αλυσίδα μικρών σφαιρών. Αντίθετα, για μια καθαρά εννοιολογική παρουσίαση χρησιμοποιούμε την αλυσίδα ράβδων και το βίντεο του πειράματος του ξύλου που βάλλεται από σφαίρα. Η αλυσίδα είναι καλύτερη εδώ, επειδή αυξάνει το υψηλότερο σημείο πάνω από το δοχείο και επειδή οι ράβδοι είναι οπτικά πιο όμοιες με τα κομμάτια ξύλου στο πείραμα της βολής.

Ο πίδακας αλυσίδας μπορεί να χρησιμοποιηθεί για να συζητηθούν θέματα σε συστήματα συνεχούς μάζας, όπως το θεώρημα ορμής, η ταχύτητα των κυμάτων και η υποκρίσιμη και υπερκρίσιμη ροή. Για διακριτά συστήματα μάζας, μπορεί να χρησιμοποιηθεί για να συζητηθούν θέματα όπως η σχέση μεταξύ των δυνάμεων και των ροπών, η περιστροφή και η μεταφορά, οι δυνάμεις αντίδρασης, το κέντρο κρούσεων και πολλά άλλα. Σε γενικές γραμμές, διαπιστώνουμε ότι η πίδακας προσφέρει πολλές ευκαιρίες διδασκαλίας.

V. ΣΥΜΠΕΡΑΣΜΑΤΑ

Σε αυτή την εργασία, για να περιγράψουμε τον πίδακα αλυσίδας έχουμε χρησιμοποιήσει την αρχή διατήρησης της ορμής και μια μορφή νόμων του Νεύτωνα για συστήματα συνεχούς μάζας. Χρησιμοποιώντας αυτή την προσέγγιση, είναι εύκολο να συναχθεί ότι η αλυσίδα ανυψώνεται πάνω από το δοχείο λόγω των ωθήσεων που δίδονται στους αλυσωτούς συνδέσμους από το δοχείο καθώς περιστρέφονται εγκαταλείποντας το οριζόντιο επίπεδο και την ηρεμία στο δοχείο. Επίσης, προκύπτει η σχέση μεταξύ της ταχύτητας αλυσίδας σε σταθερή κατάσταση και του $h_{above} / h_{below}$ . Οι ταυτόχρονες μετρήσεις της ταχύτητας της αλυσίδας και του $h_{above} / h_{below}$ , που παρουσιάζονται εδώ, υποδηλώνουν ότι οι συνέπειες οποιασδήποτε καθοδικής δύναμης στην αλυσίδα που προσκρούει στο δάπεδο, μπορούν να παραμεληθούν.

Ο υπολογισμός του $h_{above} / h_{below}$ απαιτεί ένα μοντέλο του τρόπου αλληλεπίδρασης των αλυσίδων με τον πάτο του δοχείου. Το μοντέλο που αναπτύσσεται εδώ υπερβαίνει αυτό προηγούμενων συγγραφέων, συμπεριλαμβάνοντας το πάχος των συνδέσμων και λαμβάνοντας επίσης υπόψη την εξαρτώμενη από το χρόνο κίνηση του συνδέσμου που έρχεται σε επαφή με το δάπεδο του δοχείου. Το μοντέλο δίνει μια ποσοτική πρόβλεψη για το $h_{above} / h_{below}$ στην εξίσωση (19), που δεν έχει ελεύθερες παραμέτρους και καμία ασάφεια ως προς το τι αποτελεί σύνδεσμο. Το μοντέλο δείχνει ότι ένας σύνδεσμος θα απομακρυνθεί από το δοχείο αφού περιστραφεί μόνο με μια μικρή γωνία και αυτή η κρίσιμη γωνία υπολογίζεται στην εξίσωση (18). Οι προβλέψεις του μοντέλου είναι αρκετά επιτυχείς για τις αλυσίδες μπάλας αλλά δεν είναι ιδιαίτερα ακριβείς για την αλυσίδα ράβδου. Αυτή η ανακρίβεια είναι πιθανή επειδή το μοντέλο δεν περιλαμβάνει τις επιπτώσεις της κάμψης στις διασταυρώσεις μέσα στο σύνδεσμο, οι οποίες είναι πολύ πιο σημαντικές για τους μακρύτερους συνδέσμους που αποτελούνται από ράβδους.

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr