- Των Takeshi Asal, Takao Akatsuka και Steve Haake*
- Από το Physics World
Ο Bill Shankly, πρώην διευθυντής του ποδοσφαιρικού συλλόγου της Λίβερπουλ, είπε κάποτε: “Το ποδόσφαιρο δεν είναι θέμα ζωής και θανάτου. Είναι πιο σημαντικό από αυτά.” Αυτό το μήνα στο Παγκόσμιο Κύπελλο, εκατομμύρια φίλαθλοι θα νιώσουν το ίδιο συναίσθημα για λίγες, σύντομες εβδομάδες. Στη συνέχεια, η εκδήλωση θα τελειώσει και εκείνο που θα μείνει θα είναι μερικές επαναλήψεις στην τηλεόραση και η ατελείωτη εικασία για το τι θα μπορούσε να συμβεί. Είναι αυτή η πτυχή του ποδοσφαίρου που οι οπαδοί της αγαπούν και άλλοι μισούν. Τι θα γινόταν αν έμπαινε το πέναλτι; Τι θα συνέβαινε αν ο παίκτης δεν είχε αποβληθεί; Τι θα γινόταν αν το ελεύθερο λάκτισμα δε χτυπούσε στο τείχος και έμπαινε γκολ;

Ο Ρομπέρο Κάρλος της Βραζιλίας σκοράρει κατά της Γαλλίας με ένα τέλειο κτύπημα φάουλ.
Πολλοί οπαδοί θα θυμούνται το φάουλ που εκτέλεσε ο Βραζιλιάνος Ρομπέρτο Κάρλος σε ένα τουρνουά στη Γαλλία το 1997. Η μπάλα τοποθετήθηκε περίπου 30 μέτρα από την εστία του αντιπάλου και ελαφρώς δεξιά. Ο Κάρλος κτύπησε την μπάλα ξυστά στα δεξιά ώστε να περάσει αρχικά από το τείχος των αμυντικών κατά τουλάχιστον ένα μέτρο και να υποχρεώσει έναν ποδοσφαιριστή, που στεκόταν σε απόσταση μέτρια από το τέρμα, να σκύψει το κεφάλι του. Στη συνέχεια, σχεδόν μαγικά, η μπάλα έστριψε προς τα αριστερά και μπήκε στην πάνω δεξιά γωνία του γκολπόστ, προς μεγάλη έκπληξη των παικτών, του τερματοφύλακα και των μέσων μαζικής ενημέρωσης.
Προφανώς, ο Κάρλος εκτελούσε αυτό το λάκτισμα όλη την ώρα στο γήπεδο της προπόνησης. Ένιωθε διαισθητικά πώς να καμπυλώνει την μπάλα με το χτύπημα σε μια συγκεκριμένη ταχύτητα και με μία συγκεκριμένη περιστροφή. Πιθανότατα όμως δεν γνώριζε ότι πίσω από όλα ήταν η φυσική.
Αεροδυναμική των αθλητικών σφαιρών
Η πρώτη εξήγηση της πλευρικής κάμψης ενός περιστρεφόμενου αντικειμένου πιστώθηκε στο Λόρδο Rayleigh πάνω στην εργασία του Γερμανού φυσικού Gustav Magnus το 1852. Ο Magnus προσπαθούσε πραγματικά να προσδιορίσει γιατί περιστρεφόμενα κελυφοι και σφαίρες εκτρέπονται προς τη μία πλευρά αλλά η εξήγησή του ισχύει εξίσου καλά και με τις μπάλες. Πράγματι, ο θεμελιώδης μηχανισμός μιας μπάλας που καμπυλώνεται στο ποδόσφαιρο είναι σχεδόν ο ίδιος όπως σε άλλα αθλήματα όπως το μπέιζμπολ, το γκολφ, το κρίκετ και το τένις.
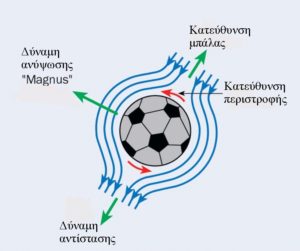
Περιστρεφόμενη μπάλα
Εξετάστε μια μπάλα που περιστρέφεται γύρω από έναν άξονα κάθετο στη ροή του αέρα και μέσα σ’ αυτόν (δείτε πάνω). Ο αέρας ταξιδεύει πιο γρήγορα σε σχέση με το κέντρο της σφαίρας εκεί όπου η περιφέρεια κινείται προς την ίδια κατεύθυνση με τη ροή του αέρα. Αυτό μειώνει την πίεση, σύμφωνα με την αρχή του Bernouilli. Το αντίθετο αποτέλεσμα συμβαίνει στην άλλη πλευρά της μπάλας, όπου ο αέρας ταξιδεύει πιο αργά σε σχέση με το κέντρο της μπάλας. Υπάρχει επομένως μια ανισορροπία στις δυνάμεις και η μπάλα εκτρέπεται – ή, όπως το έθεσε ο Sir J J Thomson το 1910, “η μπάλα ακολουθεί τη μύτη της”. Αυτή η πλευρική εκτροπή μιας μπάλας κατά την πτήση είναι γενικά γνωστή ως το “φαινόμενο Magnus”.
Οι δυνάμεις σε μια περιστρεφόμενη μπάλα που πετάει μέσα στον αέρα χωρίζονται γενικά σε δύο τύπους: τη δύναμη ανύψωσης και τη δύναμη αντίστασης. Η δύναμη ανύψωσης είναι η προς τα πάνω ή η προς τα πλάγια δύναμη που είναι υπεύθυνη για το φαινόμενο Magnus. Η δύναμη αντίστασης δρα στην αντίθετη κατεύθυνση από τη διαδρομή της μπάλας.
Ας υπολογίσουμε τις δυνάμεις στην εργασία με ένα καλά κτυπημένο ελεύθερο λάκτισμα. Υποθέτοντας ότι η ταχύτητα της σφαίρας είναι 25-30m/s (περίπου 108km/h) και ότι η περιστροφή είναι περίπου 8-10 περιστροφές ανά δευτερόλεπτο, τότε η δύναμη ανύψωσης είναι περίπου 3,5 N. Οι κανονισμοί ορίζουν ότι η μπάλα ποδοσφαίρου πρέπει να έχει μάζα 410-450g, πράγμα που σημαίνει ότι επιταχύνεται κατά περίπου 8m/s2. Και δεδομένου ότι η μπάλα θα κινηθεί για 1 δευτερόλεπτο πάνω στην τροχιά των 30 μέτρων, η δύναμη ανύψωσης θα μπορούσε να κάνει την μπάλα να αποκλίνει κατά 4 μέτρα από την κανονική της ευθεία. Αρκετά για να αντιμετωπίσει κάποιον τερματοφύλακα!
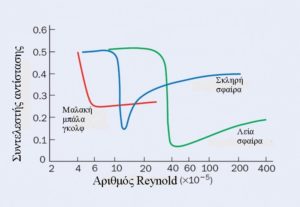
Φυσική αντίσταση
Η δύναμη αντίστασης, FΑ , σε μια σφαίρα αυξάνεται με το τετράγωνο της ταχύτητας υ, υποθέτοντας ότι η πυκνότητα ρ της σφαίρας και της περιοχής της εγκάρσιας τομής Α παραμένουν αμετάβλητες: FΑ = CΑ· ρ·A·υ2 / 2. Φαίνεται, ωστόσο, ότι ο “συντελεστής αντίστασης”, CΑ, εξαρτάται επίσης από την ταχύτητα της μπάλας. Για παράδειγμα, αν σχεδιάσουμε τον συντελεστή σε συνάρτηση με τον αριθμό Reynold – μια αδιάστατη παράμετρος ίση με ρ·υ· D / μ, όπου D είναι η διάμετρος της σφαίρας και μ είναι το κινηματικό ιξώδες του αέρα – διαπιστώνουμε ότι ο συντελεστής αντίστασης πέφτει ξαφνικά όταν η ροή αέρα στην επιφάνεια της σφαίρας αλλάζει από ομαλή και στρωτή προς στροβιλώδη (βλ. κάτω).
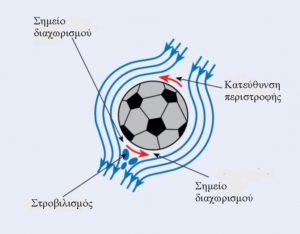
Στροβιλισμός του αέρα και αντίσταση
Όταν η ροή αέρα είναι στρωτή και ο συντελεστής αντίστασης είναι υψηλός, το οριακό στρώμα του αέρα στην επιφάνεια της σφαίρας «χωρίζει» σχετικά νωρίς καθώς ρέει πάνω από την σφαίρα, δημιουργώντας στροβίλους στο πέρασμά της. Ωστόσο, όταν η ροή αέρα είναι τυρβώδης, το οριακό στρώμα κολλάει στην μπάλα για μεγαλύτερο χρονικό διάστημα. Αυτό παράγει καθυστερημένο χωρισμό και μικρή αντίσταση.
Ο αριθμός Reynold στον οποίο πέφτει ο συντελεστής αντίστασηςς εξαρτάται συνεπώς από την τραχύτητα της επιφάνειας της μπάλας. Για παράδειγμα, οι μπάλες του γκολφ, οι οποίες είναι βαριές, έχουν αρκετά μεγάλη τραχύτητα επιφάνειας και ο συντελεστής αντίστασης πέφτει σε σχετικά χαμηλό αριθμό Reynold (~ 2 × 104). Μία μπάλα ποδοσφαίρου, ωστόσο, είναι ομαλότερη από μια μπάλα γκολφ και η κρίσιμη μετάβαση επιτυγχάνεται με έναν πολύ υψηλότερο αριθμό Reynold’s (~ 4 × 105).
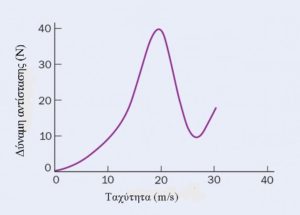
Δύναμη αντίστασης – ταχύτητα
Το αποτέλεσμα όλων αυτών είναι ότι μία αργά κινούμενη μπάλα υφίσταται μια σχετικά μεγάλη επιβραδυντική δύναμη. Αλλά αν μπορείτε να χτυπήσετε την μπάλα αρκετά γρήγορα ώστε η ροή του αέρα πάνω από αυτή να είναι στροβιλώδης, η μπάλα υφίσταται μια μικρή επιβραδυντική δύναμη (βλ. πάνω). Μία ταχύτατα κινούμενη μπάλα είναι επομένως διπλό πρόβλημα για έναν τερματοφύλακα που ελπίζει να κάνει μια απόκρουση – όχι μόνο η μπάλα κινείται με μεγάλη ταχύτητα, αλλά δεν επιβραδύνει όσο αναμένεται. Ίσως οι καλύτεροι τερματοφύλακες κατανοούν διαισθητικά περισσότερη φυσική από ό, τι νομίζουν.
Το 1976 ο Peter Bearman και οι συνεργάτες του από το Imperial College, Λονδίνο, πραγματοποίησαν μια κλασική σειρά πειραμάτων στις μπάλες του γκολφ. Διαπίστωσαν ότι η αύξηση της περιστροφής σε μια μπάλα παρήγαγε υψηλότερο συντελεστή ανύψωσης και κατά συνέπεια μεγαλύτερη δύναμη Magnus. Ωστόσο, η αύξηση της ταχύτητας σε δεδομένη περιστροφή μείωσε τον συντελεστή ανύψωσης. Αυτό σημαίνει για μία μπάλα ποδοσφαίρου ότι μπάλα αργής κίνησης με πολλή περιστροφή θα έχει μεγαλύτερη πλάγια δύναμη από μια γρήγορη μπάλα με την ίδια περιστροφή. Έτσι, καθώς μια μπάλα επιβραδύνεται στο τέλος της τροχιάς της, η καμπύλη γίνεται πιο έντονη.
Η επανεξέταση της περίπτωσης του σουτ του Ρομπέρτο Κάρλος
Πώς εξηγείται λοιπόν αυτό το ελεύθερο λάκτισμα του Roberto Carlos; Παρόλο που δεν μπορούμε να είμαστε απολύτως βέβαιοι, τα ακόλουθα είναι πιθανώς μια δίκαιη εξήγηση για το τι συνέβη.
Ο Κάρλος έδιωξε την μπάλα με το εξωτερικό του αριστερού ποδιού για να την κάνει να περιστραφεί αριστερόστροφα καθώς κοίταζε πάνω της. Οι συνθήκες ήταν στεγνές, οπότε το ποσό της περιστροφής που έδωσε στην μπάλα ήταν υψηλό, ίσως πάνω από 10 περιστροφές ανά δευτερόλεπτο. Το χτύπημα με το εξωτερικό του ποδιού του επέτρεψε να χτυπήσει σκληρά την μπάλα, πιθανότατα με ταχύτητα πάνω από 30m/s (108Km/h). Η ροή του αέρα πάνω από την επιφάνεια της μπάλας ήταν τυρβώδης, γεγονός που έδωσε στη σφαίρα μια σχετικά χαμηλή δύναμη αντίστασης. Με κάποιο τρόπο στην πορεία της – ίσως γύρω από το σημείο των 10 μέτρων (ή περίπου στη θέση του τείχους των αμυντικών) – η ταχύτητα της μπάλας έπεσε έτσι ώστε να εισέλθει στο καθεστώς στρωτής ροής. Αυτό αύξησε σημαντικά την αντίσταση στην μπάλα, γεγονός που την επιβράδυνε ακόμα περισσότερο. Αυτό επέτρεψε στην πλαγία δύναμη Magnus, η οποία έστριψε την μπάλα προς τα γκολπόστ, να γίνει ακόμα πιο αποτελεσματική. Υποθέτοντας ότι το ποσοστό περιστροφής δεν είχε μειωθεί υπερβολικά, τότε ο συντελεστής αντίστασης αυξήθηκε. Αυτό εισήγαγε μια ακόμη μεγαλύτερη πλάγια δύναμη και προκάλεσε τη στροφή της μπάλας. Τέλος, καθώς η σφαίρα επιβραδύνθηκε, η κάμψη έγινε ακόμα πιο μεγάλη (πιθανώς λόγω της αύξησης του συντελεστή ανύψωσης) μέχρι να φτάσει στο πίσω μέρος του δικτύου – προς μεγάλη χαρά των φυσικών στο πλήθος.
Η τρέχουσα έρευνα για την κίνηση της μπάλας
Υπάρχουν περισσότερα για την ποδοσφαιρική έρευνα από την απλή μελέτη της κίνησης της μπάλας κατά την πτήση της. Οι ερευνητές ενδιαφέρονται επίσης να μάθουν πώς ένας ποδοσφαιριστής χτυπά μια μπάλα. Για παράδειγμα, ο Stanley Plagenhof του Πανεπιστημίου της Μασαχουσέτης στις ΗΠΑ έχει μελετήσει τη κινηματική της κλωτσιάς – με άλλα λόγια, αγνοώντας τις εμπλεκόμενες δυνάμεις. Άλλοι ερευνητές, όπως η Elizabeth Roberts και οι συνεργάτες της στο Πανεπιστήμιο του Ουισκόνσιν, πραγματοποίησαν δυναμικές αναλύσεις του λακτίσματος, λαμβάνοντας υπόψη τις εμπλεκόμενες δυνάμεις.
Αυτές οι πειραματικές προσεγγίσεις παρήγαγαν μερικά εξαιρετικά αποτελέσματα, αν και εξακολουθούν να υπάρχουν πολλές προκλήσεις. Ένα από τα πιο κρίσιμα προβλήματα είναι η δυσκολία μέτρησης της σωματικής κίνησης των ανθρώπων, εν μέρει επειδή οι κινήσεις τους είναι τόσο απρόβλεπτες. Ωστόσο, οι πρόσφατες εξελίξεις στην ανάλυση της κίνησης με ηλεκτρονικούς υπολογιστές έχουν προσελκύσει μεγάλη προσοχή στην αθλητική επιστήμη και, με τη βοήθεια νέων επιστημονικών μεθόδων, είναι πλέον δυνατή η λήψη εύλογα ακριβών μετρήσεων της ανθρώπινης κίνησης.
Για παράδειγμα, δύο από τους συγγραφείς του παρόντος άρθρου και μια ερευνητική ομάδα στο Πανεπιστήμιο Yamagata της Ιαπωνίας χρησιμοποίησαν μια υπολογιστική επιστημονική προσέγγιση συνδυασμένη με τις πιο συμβατικές δυναμικές μεθόδους για την προσομοίωση του τρόπου με τον οποίο οι παίκτες κλωτσούν μια μπάλα. Αυτές οι προσομοιώσεις επέτρεψαν τη δημιουργία “εικονικών” ποδοσφαιριστών διαφόρων τύπων – από αρχάριους και μικρά παιδιά έως επαγγελματίες – που να παίζουν σε εικονικό χώρο και χρόνο στον υπολογιστή. Οι κατασκευαστές αθλητικού εξοπλισμού, όπως η ASICS Corporation, που χρηματοδοτούν το έργο στο Yamagata, ενδιαφέρονται επίσης για την εργασία. Ελπίζουν να χρησιμοποιήσουν τα αποτελέσματα για να σχεδιάσουν ασφαλέστερο και αποδοτικότερο αθλητικό εξοπλισμό που μπορεί να κατασκευαστεί γρηγορότερα και πιο οικονομικά από τα υπάρχοντα προϊόντα.

Πώς καμπυλώνεται η τροχιά της μπάλας
Ακολουθήθηκε η κίνηση των παικτών χρησιμοποιώντας βίντεο υψηλής ταχύτητας στα 4500 καρέ ανά δευτερόλεπτο και στη συνέχεια η επίδραση του ποδιού στην μπάλα μελετήθηκε με ανάλυση πεπερασμένων στοιχείων. Τα αρχικά πειράματα απέδειξαν ό,τι γνωρίζουν οι περισσότεροι ποδοσφαιριστές: εάν χτυπάτε την μπάλα ευθεία με το κουτουπιέ σας, έτσι ώστε το πόδι να χτυπάει τη μπάλα σε ευθεία με το κέντρο βάρους της μπάλας, τότε η μπάλα φεύγει σε ευθεία γραμμή. Ωστόσο, αν κλωτσήσετε την μπάλα με το μπροστινό μέρος του ποδιού σας και με τη γωνία μεταξύ της κνήμης και του πέλματός σας σε 90 ° (βλέπε πάνω), θα καμπυλωθεί κατά την πτήση. Σε αυτή την περίπτωση, ο δραση είναι εκτός κέντρου βάρους. Αυτό φέρνει ως αποτέλεσμα ότι η εφαρμοζόμενη δύναμη λειτουργεί ως ροπή στρέψης, η οποία επομένως δίνει στη σφαίρα περιστροφή.
Τα πειραματικά αποτελέσματα έδειξαν επίσης ότι η περιστροφή που προσλαμβάνεται από τη σφαίρα είναι στενά συνδεδεμένη με το συντελεστή τριβής μεταξύ του ποδιού και της σφαίρας και την απόσταση μετατόπισης του ποδιού από το κέντρο βάρους της μπάλας. Ένα μοντέλο πεπερασμένων στοιχείων της επίδρασης του ποδιού στην μπάλα, γραμμένο με το λογισμικό DYTRAN και PATRAN από την εταιρία MacNeal Schwendler Corporation, χρησιμοποιήθηκε για την αριθμητική ανάλυση αυτών των συμβάντων. Αυτή η μελέτη έδειξε ότι η αύξηση του συντελεστή τριβής μεταξύ της μπάλας και του ποδιού προκάλεσε στην μπάλα περισσότερη περιστροφή. Υπήρξε επίσης περισσότερη περιστροφή όταν αυξήθηκε η απόσταση μετατόπισης από το κέντρο βάρους. Παρατηρήθηκαν και δύο άλλα ενδιαφέροντα αποτελέσματα. Πρώτον, αν η απόσταση μετατόπισης αυξηθεί, τότε το πόδι άγγιξε την μπάλα για μικρότερο χρόνο και σε μικρότερη περιοχή, γεγονός που οδήγησε σε μείωση τόσο της περιστροφής όσο και της ταχύτητας της μπάλας. Υπάρχει λοιπόν μια ιδανική θέση για να χτυπήσετε την μπάλα εάν θέλετε μέγιστη περιστροφή: αν χτυπήσετε την μπάλα πάρα πολύ κοντά ή πολύ μακριά από το κέντρο βάρους, δεν θα πάρει καθόλου περιστροφή.
Το άλλο ενδιαφέρον αποτέλεσμα ήταν ότι ακόμα κι αν ο συντελεστής τριβής είναι μηδέν, η μπάλα εξακολουθεί να κερδίζει κάποια περιστροφή αν την κλωτσήσετε σε μια απόσταση από το κέντρο βάρους του. Αν και στην περίπτωση αυτή δεν υπάρχει περιφερειακή δύναμη παράλληλη με την περιφέρεια της σφαίρας (δεδομένου ότι ο συντελεστής τριβής είναι μηδέν), η σφαίρα παραμορφώνεται προς το κέντρο της, πράγμα που προκαλεί κάποια δύναμη που δρα γύρω από το κέντρο βάρους. Είναι επομένως δυνατό να περιστρέψεται την μπάλα μια βροχερή μέρα, αν και η περιστροφή θα είναι πολύ μικρότερη από ό, τι σε συνθήκες ξηρές.
Φυσικά, η ανάλυση έχει αρκετούς περιορισμούς. Ο αέρας έξω από την σφαίρα αγνοήθηκε και υποτίθεται ότι ο αέρας μέσα στην μπάλα συμπεριφέρθηκε σύμφωνα με ένα συμπιεσμένο μοντέλο ροής ρευστού. Στην ιδανική περίπτωση, ο αέρας τόσο εντός όσο και εκτός της σφαίρας θα πρέπει να συμπεριληφθεί και τα ιξώδη να υπακούουν στις εξισώσεις Navier-Stokes. Θεωρήθηκε επίσης ότι το πόδι ήταν ομοιογενές, όταν είναι προφανές ότι ένα πραγματικό πόδι είναι πολύ πιο περίπλοκο από αυτό. Αν και θα ήταν αδύνατο να δημιουργηθεί ένα τέλειο μοντέλο που να λαμβάνει υπόψη όλους τους παράγοντες, το μοντέλο αυτό περιλαμβάνει τα πιο σημαντικά χαρακτηριστικά.
Εξετάζοντας το μέλλον, δύο από εμάς (συγγραφείς του άρθρου) σκοπεύουμε επίσης να διερευνήσουμε την επίδραση διαφορετικών τύπων υποδημάτων στην κλωτσιά μιας μπάλας. Εν τω μεταξύ, η ASICS συνδυάζει τις προσομοιώσεις πεπερασμένων στοιχείων του Yamagata με τη βιο-μηχανική, τη φυσιολογία και την επιστήμη των υλικών για να σχεδιάσει νέους τύπους ποδοσφαιρικών παπουτσιών. Τελικά, όμως, ο ποδοσφαιριστής κάνει τη διαφορά – και χωρίς ικανότητα, η τεχνολογία είναι άχρηστη.
Το τελικό σφύριγμα
Τι μπορούμε να μάθουμε από τον Ρομπέρτο Κάρλος; Εάν κλωτσήσετε τη σφαίρα αρκετά σκληρά ώστε η ροή του αέρα πάνω από την επιφάνεια να γίνει στροβιλώδης, τότε η δύναμη τριβής παραμένει μικρή και η μπάλα πραγματικά θα πετάξει. Εάν θέλετε να καμπυλωθεί η μπάλα, δώστε πολύ περιστροφή κτυπώντας την μπάλα μακρυά από το κέντρο της. Αυτό είναι ευκολότερο σε μια ξηρή ημέρα από ό,τι σε μια υγρή ημέρα, αλλά μπορεί ακόμα να γίνει αυτό ανεξάρτητα από τις συνθήκες. Η μπάλα καμπυλώνεται περισσότερο όταν επιβραδύνεται σε καθεστώς στρωτής ροής, οπότε θα πρέπει να εξασκηθείτε για να βεβαιωθείτε ότι αυτή η μετάβαση συμβαίνει στη σωστή θέση – για παράδειγμα, αμέσως μετά που η μπάλα θα περάσει ένα αμυντικό τείχος. Εάν οι συνθήκες είναι υγρές, μπορείτε και πάλι να κάνετε περιστροφή, αλλά θα ήταν καλύτερα να στεγνώσετε την μπάλα (και τα παπούτσια σας).
Σχεδόν 90 χρόνια πριν, ο J J Thomson έδωσε διάλεξη στο Royal Institution του Λονδίνου για τη δυναμική των μπάλων του γκολφ. Αναφέρεται ως εξής: “Αν μπορούσαμε να δεχτούμε τις εξηγήσεις για τη συμπεριφορά της μπάλας που έδωσαν πολλοί συνεισφέροντες στην πολύ ογκώδη λογοτεχνία που συγκεντρώθηκε γύρω από το παιχνίδι … θα έπρεπε να φέρω σε σας απόψε μία νέα δυναμική και να ανακοινώσω ότι η ύλη, όταν αποτελείται από μπάλες [του γκολφ], υπακούει σε νόμους εντελώς διαφορετικού χαρακτήρα από εκείνους που διέπουν τη δράση της σε άλλες συνθήκες.” Στο ποδόσφαιρο, τουλάχιστον, μπορούμε να είμαστε σίγουροι ότι τα πράγματα έχουν προχωρήσει.
*Ο Takeshi Asal βρίσκεται στην Παιδαγωγική Σχολή του Πανεπιστημίου Yamagata, Yamagata-City, Ιαπωνία. Ο Takao Akatsuka είναι στην Πολυτεχνική Σχολή του Πανεπιστημίου Yamagata, Yamagata-City, Ιαπωνία. Ο Steve Haake βρίσκεται στο Κέντρο Αθλητισμού και Άσκησης, στο Πανεπιστήμιο Sheffield Hallam του Ηνωμένου Βασιλείου
Γιάννης Γαϊσίδης
