Το δίλημμα του Ταρζάν

Εικ. 1

…πριν καταπιαστήτε με το πρόβλημα.

Σκοπός αυτής της διαδικασίας είναι να έλθουν σε επαφή οι μαθητές, που τους ενδιαφέρει η Φυσική, με θεωρητικούς υπολογισμούς τους οποίους μπορούν να κάνουν αν έχουν γνώσεις για τις βολές και μάλιστα για την πλάγια. Η αλήθεια είναι ότι από τη διδακτέα ύλη των Λυκείων η πλάγια βολή έχει αφαιρεθεί και το μόνο που υπάρχει από τις βολές είναι η οριζόντια, την οποία διδάσκονται οι μαθητές της Β´ Λυκείου στη Φυσική ΓΠ. Θα μπορούσαν επίσης να ασχοληθούν με το πρόβλημα και οι πρωτοετείς φοιτητές θετικών επιστημών και γενικά ο καθένας που τον ενδιαφέρει να κάνει μία μικρή εξάσκηση σε απλές θεωρητικές γνώσεις Φυσικής και λίγων μαθηματικών επιπέδου Γ´ Λυκείου ή πρώτου πανεπιστημιακού έτους.

Το λεγόμενο “Δίλημμα του Ταρζάν” μπορεί κανείς να το βρει σε αρκετές εκδοχές και προσεγγίσεις. Σας παρουσιάζω μια αρκετά εκλαϊκευμένη προσέγγιση από το περιοδικό The Physics Teacher της Αμερικάνικης Ένωσης Καθηγητών Φυσικής (AAPT) που αναπτύσσεται στο τεύχος του Νοεμβρίου 2013 από τους Matthew Rave και Marcus Sayers του πανεπιστημίου Western Carolina. Ως συνοδευτικό του άρθρου έχω προσθέσει και ένα αρχείο excel στο οποίο ενσωμάτωσα τους απαραίτητους μαθηματικούς τύπους για την κατασκευή του διαγράμματος που περιγράφει το άρθρο των δύο καθηγητών.

Το “Δίλημμα του Ταρζάν” θα μπορούσε να αποτελέσει και θέμα για ένα ενδιαφέρον project προς μαθητές της Β´ Λυκείου, όπου, με την καθοδήγηση του καθηγητή τους θα προσεγγίσουν το πρόβλημα βήμα-βήμα θεωρητικά και θα ασχοληθούν επίσης και με την κατασκευή του σχετικού φύλλου εργασίας στο excel. Με τον τρόπο αυτόν θα προάγουν ταυτόχρονα τις γνώσεις τους στη Φυσική, στο κεφάλαιο των βολών, και τις γνώσεις τους στην κατασκευή και το χειρισμό των φύλλων εργασίας στο Excel.

Το πρόβλημα

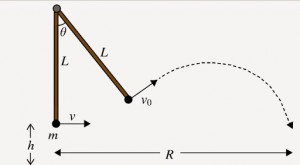
Υποθέτουμε ότι ο Ταρζάν τρέχει προς ένα κλήμα το οποίο κρέμεται κατακόρυφα από ένα δέντρο (Εικ. 1). Σκοπός είναι να περάσει πάνω από ένα φαράγγι. Σε ποιο σημείο της αιώρησής του αφήνει το κλήμα ώστε να μεγιστοποιήσει τις πιθανότητες να το περάσει;

Αυτό το λέμε “δίλημμα” γιατί υπάρχουν δύο αντικρουόμενοι παράγοντες. Από τη μία, όσο πιο γρήγορα αφήσει το κλήμα τόσο μεγαλύτερη ταχύτητα θα έχει. Από την άλλη, όσο πιο πολύ το κρατήσει τόσο πιο μακρυά μέσα στο φαράγγι θα πάει και τόσο πιο μεγάλη αρχική γωνία εκτόξευσης θα έχει αποκτήσει, όταν θα αφήσει το κλήμα. Το ερώτημα είναι: ποια γωνία εγκατάλειψης μεγιστοποιεί την οριζόντια διαδρομή του (βεληνεκές);

Θεωρητικό υπόβαθρο

Μια πρώτη εκτίμηση που μπορεί να κάνει ένας μαθητής, που έχει ασχοληθεί με τις πλάγιες βολές, είναι ότι η αναζητούμενη γωνία πρέπει να είνσι 45⁰. Αυτή είναι πράγματι η γωνία που μεγιστοποιείται το βεληνεκές μιας πλάγιας βολής που ξεκινάει και τελειώνει πάνω στην ίδια οριζόντια επιφάνεια. Όμως εδώ τα πράγματα δεν είναι ακριβώς έτσι.

Απαιτούνται κατ’ αρχήν ορισμένες υποθέσεις που πρέπει να κάνουμε. Υποθέτουμε ότι το κλήμα είναι αβαρές και παραμένει τεντωμένο καθ’ όλη τη διάρκεια της κίνησής του. Το μήκος του είναι L και η κάτω άκρη του αρχικά βρίσκεται σε ύψος h πάνω από το έδαφος. Υποθέτουμε ότι ο Ταρζάν είναι σημειακή μάζα m και κρατάει το κάτω άκρο του κλήματος. (Αυτό μπορούνε να το υποθέσουμε αν δεχτούμε ότι το κέντρο μάζας του βρίσκεται στο ίδιο επίπεδο με το κάτω άκρο του κλήματος ανεξάρτητα από πού το έχει πιάσει). Υποθέτουμε επίσης μια αρχική οριζόντια ταχύτητα v. Θέλουμε να μεγιστοποιήσουμε την οριζόντια απόσταση μέχρι να έλθει ο Ταρζάν και πάλι σε επαφή με το έδαφος, όπως τη μετρούμε από την αρχική θέση της μάζας m επί του κάτω άκρου του κλήματος και όχι από το σημείο που εγκαταλείπει το κλήμα. Αυτό σημαίνει ότι δε μας ενδιαφέρει το πλάτος του φαραγγιού, εκτός κι αν θέλουμε να δούμε αν ο Ταρζάν πέφτει τελικά μέσα στο φαράγγι ή έξω από αυτό. Τέλος θεωρούμε τις τριβές και τις αντιστάσεις του αέρα αμελητέες.

Ας θυμηθούμε τώρα τους τύπους της πλάγιας βολής. Για μία πλάγια βολή που γίνεται από το έδαφος με αρχική ταχύτητα v₀ και υπό γωνία θ ως προς το έδαφος έχουμε τη σχέση:

(1) $\begin{equation*} R=\frac{v_0^2 \cdot \eta \mu 2 \theta}{g} \end{equation*}$

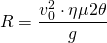
Όπου R είναι το οριζόντιο βεληνεκές με g=9,8m/s².

Ας θεωρήσουμε τώρα ότι η ίδια βολή γίνεται, όχι από το έδαφος, αλλά από ύψος H. Αυτό είναι ένα πρόβλημα κινηματικής δύο διαστάσεων και παίρνουνε τις εξής εκφράσεις:

Κατά τον κατακόρυφο άξονα y έχουμε την εξίσωση:

(2) $\begin{equation*} \Delta y=v_0 \cdot \Delta t+ \frac{1}{2}a_y \cdot ( \Delta t)^2 \end{equation*}$

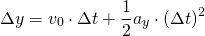
Που μας δίνει:

(3) $\begin{equation*} H=-(v_0 \cdot \eta \mu \theta) \cdot \Delta t+\frac{1}{2} g \cdot ( \Delta t)^2 \Leftrightarrow \frac{1}{2} g \cdot ( \Delta t)^2-(v_0 \cdot \eta \mu \theta) \cdot \Delta t-H=0 \end{equation*}$

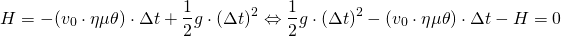
Η τελευταία σχέση είναι β΄ βαθμού εξίσωση ως προς Δt που μας δίνει τη λύση (αφού έχουμε απορρίψει την αρνητική):

(4) $\begin{equation*} \Delta t= \frac{v_0 \cdot \eta \mu \theta + \sqrt{(v_0 \cdot \eta \mu \theta)^2+2gH}}{g} \end{equation*}$

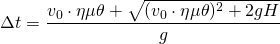
Επομένως το οριζόντιο βεληνεκές μιας τέτοιας βολής θα είναι:

(5) $\begin{equation*} R=v_{0x} \cdot \Delta t=v_0 \cdot \sigma \upsilon \nu \theta \cdot \left( \frac{v_0 \cdot \eta \mu \theta + \sqrt{(v_0 \cdot \eta \mu \theta)^2+2gH}}{g} \right) \end{equation*}$

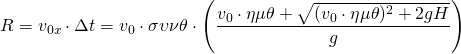
Είναι χρήσιμο να πούμε ότι αν είναι H=0 τότε η (5) μεταπίπτει στην (2)

Επομένως το ζητούμενο είναι να βρούμε για ποια τιμή της θ μεγιστοποιείται η (5).
Ένας τρόπος είναι να πάρουμε την παράγωγο του R ως προς θ (dR/dθ) και να έξισώσουμε με μηδέν. Αυτό όμως περιέχει ανυπέρβλητες δυσκολίες για το επίπεδο των μαθητών μας.
Μπορούμε όμως να δώσουμε λύση με τη χρήση απλά και μόνον του Excel.

Το Δίλημμα του Ταρζάν: η λύση

Τώρα είμαστε έτοιμοι να πάμε στο πρόβλημα.

Επειδή δε γνωρίζουμε την ταχύτητα v₀ με την οποία ο Ταρζάν εγκαταλείπει το κλήμα, εφαρμόζουμε τη διατήρηση της μηχανικής ενέργειας στις δύο καταστάσεις: Όταν το κλήμα βρίσκεται στην κατακόρυφη θέση (1) και όταν έχει γράψει γωνία θ τη στιγμή που το εγκαταλείπει ο Ταρζάν (εικ. 2).

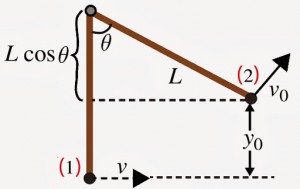
Εικ. 2

(6) $\begin{equation*} \frac{1}{2}m \cdot v^2=m \cdot g \cdot y_0+\frac{1}{2}m \cdot v_0^2 \end{equation*}$

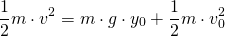
Λύνοντας την (6) ως προς v₀ έχουμε:

$v_0= \sqrt{v^2-2gy_0}$

Αλλά επειδή είναι:

$y_0=L-L \cdot \sigma \upsilon \nu \theta$

Η ταχύτητα v₀ θα γίνει:

(7) $\begin{equation*} v_0= \sqrt{v^2-2gL+2gL \sigma \upsilon \nu \theta} \end{equation*}$

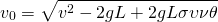
Είναι χρήσιμο να υποθέσουμε στο σημείο αυτό ότι ο Ταρζάν έχει επαρκή αρχική ταχύτητα v ώστε να είναι σε θέση να πιάσει οποιαδήποτε γωνία θ μεταξύ των 0⁰ και 90⁰.

Το οριζόντιο βεληνεκές από το σημείο διαφυγής του Ταρζάν (έστω R₂) προκύπτει με αντικατάσταση της v₀ από την (7) στην (5). Η λύση στο πρόβλημα – που είναι το μήκος R₁ που το μετράμε από την κατακόρυφη θέση (1), εικ. 2 – είναι απλά το άθροισμα Lημθ+R₂. Το τελικό αποτέλεσμα που προκύπτει είναι:

(8) $\begin{equation*} \begin{split} R & =L \eta \mu \theta +\sqrt{v^2-2gL+2gL \sigma \upsilon \nu \theta} \cdot \sigma \upsilon \nu \theta \\ & \cdot \left ( \frac{\sqrt{v^2-2gL+2gL \sigma \upsilon \nu \theta} \cdot \eta \mu \theta + \sqrt{v^2-2gL+2gL \sigma \upsilon \nu \theta \cdot \eta \mu^2 \theta +2gH}}{g} \right) \end{split} \end{equation*}$

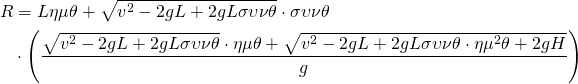
Όπου στη σχέση (7) έχουμε θέσει H=h+y₀=h+L-Lσυνθ. Αυτό το βεληνεκές, ως συνάρτηση της γωνίας θ, πρέπει να γίνει γραφική παράσταση στο Excel θέτοντας λογικές τιμές στις παραμέτρους v, h και L. Από τη γραφική παράσταση θα φανεί σε ποια γωνία θα υπάρχει η μέγιστη τιμή του βεληνεκούς και πόση θα είναι αυτή.

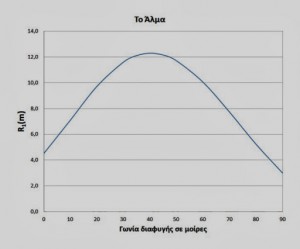
Στην παρακάτω εικόνα φαίνεται το αποτέλεσμα για v=10m/s, h=1m και L=3m.

Από εδώ μπορείτε να πάρετε το φύλλο

εργασίας στο Excel

Η μεγιστοποίηση γίνεται κοντά στη γωνία 40⁰ , για τις τιμές των παραμέτρων που φαίνονται πιο πάνω.

Στο φύλλο Excel έχουμε δώσει τιμές στη θ από 0⁰ έως 90⁰, με βήμα 10⁰. Από 30⁰ έως 50⁰ δίνουμε βήμα 5⁰ γιατί σ’ αυτήν την περιοχή γωνιών αναμένουμε τη μεγιστοποίηση του βεληνεκούς και επομένως όσο μικραίνουμε το βήμα τόσο μεγαλύτερη ακρίβεια επιτυγχάνουμε. Βεβαίως τη μεγαλύτερη ακρίβεια, τονίζουμε και πάλι, την επιτυγχάνουμε με μηδενισμό της πρώτης παραγώγου (dR₁/dθ=0) και επίλυση της εξίσωσης ως προς θ. Τούτο όμως απαιτεί αριθμητικές μεθόδους, τις οποίες δεν εξετάζουμε εδώ.

Διερεύνηση της λύσης

Ας εξετάσουμε τώρα ορισμένες οριακές περιπτώσεις.

Αν η αρχική ταχύτητα του Ταρζάν τη στιγμή που γραπώνει το κλήμα γίνει πολύ μεγάλη, δηλαδή να τείνει προς το άπειρο, τότε η γωνία διαφυγής τείνει προς τις 45⁰. Δοκιμάστε το στον πίνακα τιμών βάζοντας τη v π.χ. 250m/s. Αμέσως θα δείτε ότι στον κάτω πίνακα παίρνουμε ως λύση 45⁰,δηλαδή τη γωνία που προβλέπει η θεωρία μας για τη μεγιστοποίηση του βεληνεκούς σε πλάγια βολή που πραγματοποιείται από ύψος μηδέν. Αυτό όμως είναι αναμενόμενο γιατί στην περίπτωση αυτή η ταχύτητα του Ταρζάν δεν επιρρεάζεται σημαντικά από την περιστροφή του κλήματος και επομένως η γωνία θ δεν παίζει κανέναν ρόλο.

Μια άλλη διαπίστωση που μπορεί να κάνει κανείς είναι ότι αν μειώσουμε την αρχική ταχύτητα κάτω από ένα όριο οι τιμές του βεληνεκούς αρχίζουν να παρουσιάζουν κενά. Άρα υπάρχει κάποιο ελάχιστο όριο αρχικής ταχύτητας κάτω της οποίας το κλήμα δεν μπορεί να ανέβει μέχρι 90⁰. (Δοκιμάστε π.χ. v=5m/s). Πώς υπολογίζουμε αυτή την ελάχιστη τιμή ταχύτητας. Πολύ απλά, με τη διατήρηση της μηχανικής ενέργειας παίρνοντας ως γωνία διαφυγής 90⁰ και L=3m, ενώ ως ταχύτητα διαφυγής v₀ παίρνουμε την οριακή τιμή μηδέν. Έχουμε:

$v_{min}= \sqrt {2gL}=7,67m/s$

Επομένως για αρχικές ταχύτητες κάτω του 7,67m/s δεν μπορούμε να έχουμε γωνία διαφυγής 90⁰.

Τι συμβαίνει με τις τιμές των h και L;

Δοκιμάστε να βάλετε στο L τιμές μεγάλες, π.χ. 20m. Θα παρατηρήσετε ότι και πάλι μερικές τιμές βεληνεκούς χάνονται. Τούτο συμβαίνει γιατί όσο μεγαλώνει το μήκος του κλήματος L απαιτείται όλο και μεγαλύτερη αρχική κινητική ενέργεια και από ένα σημείο και μετά δεν επαρκεί για να ισοσταθμίσει τη δυναμική ενέργεια που απαιτείται για διαφυγή σε ορισμένη γωνία.

Για το h θα παρατηρήσετε ότι όσο αυξάνετε, η γωνία διαφυγής θ μειώνεται. Και αν το ύψος h τείνει προς το άπειρο, η γωνία θα τείνει προς το μηδέν. Μπορούμε δηλαδή να πούμε ότι “όσο πιο ψηλός είσαι, τόσο πιο γρήγορα πρέπει να αφήσεις το κλήμα”.

Γιάννης Γαϊσίδης

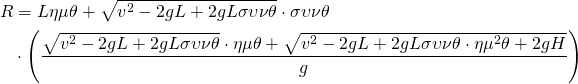
gaisidis@viewonphysics.gr