Η έννοια της δύναμης

Για να εμπεδώσεις καλύτερα την έννοια της δύναμης, δες πρώτα μία παρουσίαση με Power Point κάνοντας κλικ εδώ

1. Σημειώστε με Σ τη σωστή και με Λ τη λάθος πρόταση:
   1. Η δύναμη προκαλεί μεταβολή στη θερμοκρασία των σωμάτων.
   2. Η παραμόρφωση είναι αποτέλεσμα της επίδρασης της δύναμης.
   3. Για να σταματήσει ένα σώμα που κινείται πρέπει να ασκηθεί επάνω του δύναμη.
   4. Αν ασκηθεί δύναμη πάνω σ’ ένα σώμα που κινείται τότε μπορεί να αυξηθεί η ταχύτητά του.
   5. Σ’ ένα σώμα που ασκείται μία δύναμη το σώμα είναι δυνατόν να μην αλλάξει ταχυτήτητα ούτε να παραμορφωθεί.
2. Η μπάλα του μπιλιάρδου (1) ακολουθεί την πορεία που δείχνει το βελάκι και πέφτει πάνω στην ακίνητη μπάλα (2). Μετά τη σύγκρουση (περιοχή Α) οι μπάλες διαχωρίζονται και ακολουθούν τις πορείες που δείχνουν τα βελάκια στην περιοχή Β. Εμφανίστηκαν δυνάμεις μεταξύ των δύο σφαιρών; Αν ναι, σε ποια περιοχή; Ποια  ήταν τα αποτελέσματα των δυνάμεων αυτών;   
   

   Άσκηση 2

3. Ένα ακίνητο ελατήριο είναι κατακόρυφο και στερεωμένο στο πάνω άκρο του, ενώ στην άλλη άκρη είναι κρεμασμένο ένα μικρό σώμα (2)  Ποια μορφή θα είχε το ελατήριο αν δεν είχαμε κρεμάσει το σώμα; Επιλέξτε τη σωστή απάντηση από τα σχήματα (1) ή (3).
   

   Άσκηση 3

4. Ένα σώμα κινείται ευθύγραμμα. Όταν βρίσκεται στη θέση Α κινείται όπως δείχνει το βελάκι με ταχύτητα 20km/h. Όταν περνάει από τη θέση Β η ταχύτητα γίνεται 50km/h. Ασκήθηκε δύναμη στο σώμα; Γιατί;
   

   Άσκηση 4

5. Είναι δυνατόν ένα σώμα να δέχεται την επίδραση μιας δύναμης και ταυτόχρονα το σώμα αυτό να μην ασκεί δύναμη σε άλλο;
6. Ο άνδρας και η γυναίκα τραβούν τις άκρες του ίδιου σχοινιού. Στις εικόνες Α, Β, Γ και Δ είναι σχεδιασμένα τα διανύσματα των δυνάμεων. Σε ποια εικόνα εμφανίζονται οι δυνάμεις(τάσεις) που ασκούνται:
   1. Στα χέρια του άνδρα και της γυναίκας;
   2. Στις άκρες του σχοινιού;  
      

      Άσκηση 6

7. Αντιστοιχίστε τα διανύσματα των δυνάμεων με τις τιμές τους:  
   

   Άσκηση 7

8. Με κλίμακα 5Ν/1cm (δηλ. 5Ν για κάθε 1cm) σχεδιάστε δύο δυνάμεις 15Ν και 20Ν.
9. Το μήκος του διανύσματος μιας δύναμης είναι 8cm και την κλίμακα σχεδιασμού την πήραμε 10Ν/1cm. Πόσα Ν είναι η δύναμη που σχεδιάσαμε;
10. Η κλίμακα που χρησιμοποιήσαμε για να σχεδιάσουμε την παρακάτω δύναμη είναι 20Ν/1cm. Μπορείτε να υπολογίσετε πόση είναι η δύναμη σε Ν;   
    

    Άσκηση 10

11. Η μικρή σφαίρα του σχήματος περιστρέφεται σε κατακόρυφο επίπεδο, δεμένη στην άκρη τεντωμένου σχοινιού, του οποίου η άλλη άκρη είναι καρφωμένη στο Ο. Στη θέση που φαίνεται στο σχήμα, πάνω στη σφαίρα, ασκούνται δύο δυνάμεις, που τις παριστάνουμε με δύο διανύσματα (βελάκια) W και Τ. Μπορείτε να βρείτε ποια σώματα ασκούν αυτές τις δύο δυνάμεις πάνω στη σφαίρα; Ασκεί η σφαίρα ταυτόχρονα δυνάμεις πάνω σε άλλα σώματα; Αν ναι, πάνω σε ποια; Μπορείτε να τις σχεδιάσετε; Πώς ονομάζουμε τη δύναμη που παριστάνεται με W και πως την Τ;   
    

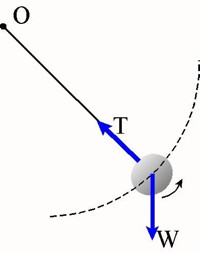
    Άσκηση 12

12. Στο σχήμα της προηγούμενης άσκησης (11) χαρακτηρίστε ποια δύναμη ασκείται εξ επαφής πάνω στη σφαίρα και ποια εξ αποστάσεως.
13. Στο παρακάτω σχήμα η μικρή σφαίρα της άσκησης 11 περνάει από το ανώτατο σημείο της τροχιάς της. Σχεδιάστε, στη θέση αυτή, τις δυνάμεις που δέχεται η σφαίρα, αναφέροντας από που προέρχεται η κάθε μία. 
    

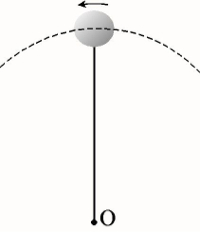
    Άσκηση 13

14. Η ράβδος ΑΓ είναι οριζόντια και στην άκρη Α είναι στερεωμένη στον τοίχο ενώ η άκρη της Γ είναι δεμένη με ένα τεντωμένο σχοινί. Σε ποιο από τα τρία σημεία Α,Γ ή Κ θα βάζατε το σημείο εφαρμογής της δύναμης του βάρους και σε ποιο της τάσης του σχοινιού; Σχεδιάστε αυτές τις δύο δυνάμεις που ασκούνται πάνω στη ράβδο και χαρακτηρίστε ποια ασκείται εξ αποστάσεως και ποια εξ επαφής.
    

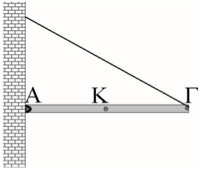
    Άσκηση 14

15. Μία σιδερένια σφαίρα κρέμεται από ένα τεντωμένο νήμα, του οποίου η άλλη άκρη Ο είναι καρφωμένη. Η σφαίρα μπορεί να περιστραφεί σε κατακόρυφο επίπεδο. Κοντά στη σφαίρα υπάρχει ένας μαγνήτης, ο οποίος την έλκει και φέρνει τη σφαίρα και το νήμα στη θέση που φαίνεται στο σχήμα, όπου το σύστημα ακινητοποιείται. Πάνω στη αφαίρα έχουν σχεδιαστεί τρεις δυνάμεις. Μπορείτε να βρείτε από πού προέρχεται η κάθε μία και ποια ασκείται εξ αποστάσεως και ποια εξ επαφής;
    

    Άσκηση 15

16. Η σφαίρα ακουμπάει στο δάπεδο και είναι ακίνητη. Πάνω της ασκούνται οι δυνάμεις W και N. Από πού προέρχεται η κάθε μία. Ποια ασκείται εξ επαφής και ποια εξ αποστάσεως; Ασκεί δυνάμεις η σφαίρα πάνω σε άλλα σώματα;  
    

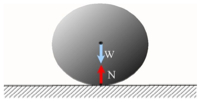
    Άσκηση 16

17. Στην εικόνα φαίνεται το ελατήριο σε δύο καταστάσεις. Πάνω, βρίσκεται σε θέση “φυσικού μήκους”, δηλαδή χωρίς να ασκείται σε αυτό οποιαδήποτε δύναμη. Κάτω το έχουμε τραβήξει με ένα σχοινί και του δώσαμε επιμήκυνση. Στην κάτω θέση να σχεδιάσετε δύο δυνάμεις: α) Τη δύναμη που δέχεται η δεξιά άκρη του ελατηρίου και β) τη δύναμη που δέχεται το χέρι μας.   
    

    Άσκηση 17

18. Να σχεδιάσετε στην παρακάτω εικόνα τη δύναμη που δέχεται το χέρι μας από το ελατήριο, όταν το ελατήριο βρίσκεται σε κατάσταση συσπείρωσης. 
    

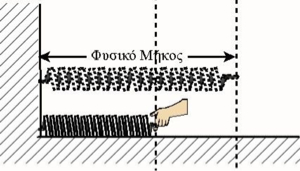
    Άσκηση 18

19. Το ελατήριο στην παρακάτω εικόνα είναι κρεμασμένο κατακόρυφα και εμφανίζεται σε τρεις κατάστασεις. Σε θέση φυσικού μήκους, σε θέση επιμήκυνσης, με κρεμασμένο ένα βάρος 10N και πάλι σε θέση επιμήκυνσης, με κρεμασμένο τώρα ένα βάρος 20N. Σημειώνονται επίσης και τα μήκη του ελατηρίου στις δύο πρώτες περιπτώσεις. Στη θέση φυσικού μήκους το ελατήριο έχει μήκος 40cm και στη θέση όπου έχει κρεμασθεί βάρος 10Ν το μήκος είναι 52cm. Υπολογίστε το μήκος του ελατηρίου όταν κρεμάμε βάρος 20N.      
    

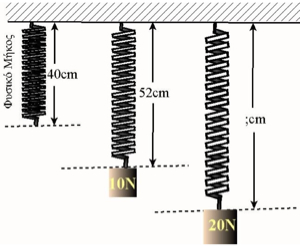
    Άσκηση 19

20. Σε ένα κατακόρυφο ελατήριο κρεμάμε διαδοχικά βάρη και σημειώνουμε τις επιμηκύνσεις. Έχοντας υπόψη το νόμο των ελαστικών παραμορφώσεων του Hook, συμπληρώστε τις τιμές που λείπουν από τον παρακάτω πίνακα.   
    

    Άσκηση 20

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr