Ο Νόμος της Παγκόσμιας Έλξης του Νεύτωνα δε διδάσκεται σε καμία τάξη του Γυμνασίου και Λυκείου. Παρόλα αυτά οι μαθητές πρέπει να διακρίνουν τη μάζα από το βάρος, να γνωρίζουν τι εννοούμε με την λέξη “βαρύτητα” και τι όταν συζητάμε για συνθήκες έλλειψης της βαρύτητας.
Αν και μέχρι σήμερα ακόμη δε γνωρίζουμε τον ακριβή μηχανισμό της βαρυτικής αλληλεπίδρασης και δεν έχουμε ιδέα πώς λειτουργεί, απαιτούμε από τους μαθητές να αντιληφθούν, γιατί οι αστροναύτες αιωρούνται μέσα στο δορυφορικό θάλαμο και γιατί η Σελήνη δεν πέφτει ποτέ πάνω στη Γη, παρόλο που τη σέρνουμε διαρκώς μαζί μας. Η συνήθης απάντηση των μαθητών μας είναι ότι οι αστροναύτες βρίσκονται εκτός της ατμόσφαιρας ή ότι βρίσκονται πολύ μακρυά από τη Γη και δεν φτάνει μέχρι εκεί η έλξη της, όπως και η Σελήνη.
Η βαρύτητα είναι μια δύναμη που ασκείται μεταξύ οποιωνδήποτε δύο μαζών στο σύμπαν. Δεν υπάρχει πιο οικεία προς εμάς δύναμη από την έλξη που τραβά το σώμα μας, τα σπίτια μας και ό, τι άλλο υπάρχει στη ζωή μας, προς τον πλανήτη Γη από κάτω μας. Ακόμη και στην περίπτωση των αστροναυτών αυτή υπάρχει σε αφθονία. Η επίδραση της βαρύτητας απλώς συγκαλύπτεται από την κίνηση τους, καθώς περιφέρονται γύρω από τον πλανήτη. Μόνη διέξοδος είναι το βαθύ διάστημα, πέρα από την περιοχή των πλανητών ή των αστέρων, όπου μπορεί πραγματικά να ξεφύγει κανείς από τη βαρύτητα.
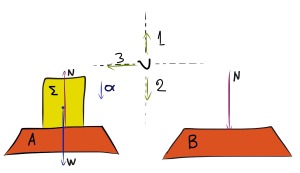
Εικ. 1. Στο σώμα Σ, που βρίσκεται στη ζυγαριά, ασκούνται δύο δυνάμεις: Η έλξη της Γης w και η δύναμη N της ζυγαριάς (Α). Η ζυγαριά, με τη σειρά της, δέχεται από το σώμα Σ την αντίθετη δυναμη της Ν, λόγω της Δράσης-Αντίδρασης από τον 3ο Νόμο του Νεύτωνα (Β). Αυτή είναι η δύναμη που μετράει η ζυγαριά. Όταν η Ν μηδενιστεί το σώμα Σ αιωρείται.
Γενικότερα, η αίσθηση του βάρους που βιώνουμε στην καθημερινή ζωή είναι ακριβώς η αίσθηση του να στηριζόμαστε στο έδαφος, καθώς αυτό ασκεί πάνω μας κάθετες δυνάμεις, που εμείς αντιλαμβανόμαστε. Με λίγα λόγια όταν διαβάζουμε τα κιλά ενός σώματος Σ στη ζυγαριά, στην πραγματικότητα μετράμε την κάθετη δυναμη N που ασκεί το Σ πάνω στη ζυγαριά (εικ. 1, B), ως αντίδραση στην αντίθετη δυναμη N που ασκεί η ζυγαριά (εικ. 1, Α) πάνω στο Σ (Δράση-Αντίδραση). Αν μπορέσουμε με κάποιο τρόπο να μηδενίσουμε τη δυναμη Ν τότε προφανώς έχουμε πετύχει συνθήκες έλλειψης βαρύτητας, γιατί το Σ ούτε θα δέχεται ούτε θα ασκεί δύναμη στο δάπεδο (ζυγαριά).
Πώς όμως μπορούμε να το καταφέρουμε αυτό; Με έναν πολύ απλό τρόπο. Αρκεί να επιταχύνουμε το σύστημα Σώμα-Δάπεδο κατακόρυφα προς τα κάτω. Προσέξτε, λέμε να “επιταχύνουμε” όχι να “κινήσουμε” προς τα κάτω. Στο σημείο όμως αυτό ας μιλήσουμε λίγο για τις δύο έννοιες:
Επιτάχυνση και ταχύτητα
Μία από τις μεγαλύτερες δυσκολίες που συναντούν οι μαθητές των γυμνασίων και των λυκείων είναι η διάκριση μεταξύ της ταχύτητας και της επιτάχυνσης. Συνήθως ταυτίζουν τις δύο έννοιες και στην καλύτερη περίπτωση πιστεύουν ότι συμπεριφέρονται με τον ίδιο τρόπο. Δηλαδή πιστεύουν ότι, αν π.χ. αυξάνεται ή μειώνεται η ταχύτητα πρέπει υποχρεωτικά να αυξάνεται ή να μειώνεται και η επιτάχυνση. Αν όμως αντιληφθούν ότι άλλο η ταχύτητα, που απαντάει στο ερώτημα “πόσο γρήγορα κινείται κάτι” και άλλο η επιτάχυνση,που απαντάει στο ερώτημα “πόσο γρήγορα αλλάζει η ταχύτητα”, τότε έχει γίνει ένα πρώτο βήμα προς τη διάκριση και κατανόηση των δύο εννοιών.
Στην εικ. 1 φαίνονται τρεις κατευθύνσεις της ταχύτητας 
και μία κατεύθυνση της επιτάχυνσης 
για το σύστημα Σώμα-Δάπεδο. Η ταχύτητα εμφανίζεται με τις κατευθύνσεις: (1), κίνηση κατακόρυφη προς τα πάνω, (2), κίνηση κατακόρυφη προς τα κάτω και (3), οριζόντια κίνηση, ενώ η επιτάχυνση εμφανίζεται ως κατακόρυφη προς τα κάτω, όπως ακριβώς η έλξη της Γης.
Στην περίπτωση (1), έχουμε την ταχύτητα και την επιτάχυνση με αντίθετες κατευθύνσεις, οπότε το σύστημα επιβραδύνεται (φρενάρει) κινούμενο προς τα πάνω.
Στην περίπωση (2) έχουμε την ταχύτητα και την επιτάχυνση με ίδιες κατευθύνσεις, οπότε το σύστημα επιταχύνεται κινούμενο προς τα κάτω.
Στην περίπτωση (3) έχουμε την ταχύτητα και την επιτάχυνση με κάθετες κατευθύνσεις. Το σύστημα τώρα περιστρέφεται σε κλειστή τροχιά γύρω από από ένα κέντρο (κεντρομόλος επιτάχυνση). Αυτό κάνουν οι δορυφόροι γύρω από τη Γη ή η Σελήνη που παραμένει μόνιμα “κολλημένη” στο ταξίδι της Γης γύρω από τον Ήλιο.
Και στις τρεις αυτές περιπτώσεις κίνησης – επιβραδυνόμενη προς τα πάνω, επιταχυνόμενη προς τα κάτω, κλειστή τροχιά – είναι δυνατόν να επιτευχθεί μηδενισμός της δύναμης Ν, που αλληλεπιδρά το σώμα Σ με το δάπεδο και άρα συνθήκες έλλειψης βαρύτητας. Ιδού γιατί.
Εφαρμόζοντας το Δεύτερο Νόμο του Νεύτωνα στο σώμα Σ έχουμε:
(1) 
Από τη σχέση (1) προκύπτει ότι αν η επιτάχυνση του συστήματος 
γίνει ίση με την επιτάχυνση της βαρύτητας 
, αν δηλαδή δώσουμε στο σύστημα κατακόρυση επιτάχυνση προς τα κάτω ίση με g, τότε ανεξαρτήτως της ταχύτητάς του, η δύναμη αλληλεπίδρασης με το δάπεδο μηδενίζεται και έχουμε συνθήκες έλλεψης βαρύτητας.
Όταν λοιπόν βλέπουμε τους αστροναύτες να πετούν μέσα στο θαλαμίσκο τους ικανοποιείται η συνθήκη αυτή και είμαστε στην περίπτωση (3) της εικ. 1, όπου η ταχύτητα είναι κάθετη προς την επιτάχυνση, αφού περιστρέφονται γύρω από τη Γη με “κεντρομόλο επιτάχυνση” ίση με την επιτάχυνση της βαρύτητας g.
“Κομήτες που ξερνάς”
Αν και τα διαστημικά ταξίδια είναι ο μόνος τρόπος που δίνει τη δυνατότητα μεγάλης χρονικής περιόδου συνθηκών έλλειψης βαρύτητας, μία πολύ φθηνότερη και πρακτικότερη μεθοδος είναι μία βόλτα πάνω σε ένα αεροπλάνο που πετάει σε παραβολική τροχιά (εικ. 2). Τέτοιου είδους αεροπλάνα, με το παρατσούκλι “κομήτες που ξερνάς”, λόγω της ζάλης που επιφέρουν, επιτρέπουν στους επιβάτες να αιωρούνται για λίγα λεπτά, ενώ το αεροπλάνο βρίσκεται πάνω στην τροχιά του παραβολικού τόξου. Οι αστροναύτες χρησιμοποιούν αυτή τη μέθοδο για να εκπαιδεύονται για τις διαστημικές πτήσεις.
Εικ. 2. Ειδικά διαμορφωμένα αεροπλάνα πετούν σε παραβολικές τροχιές και δημιουργούν στους επιβάτες συνθήκες έλλειψης βαρύτητας χωρίς να χρειάζεται να απομακρυνθούν από τη Γη.
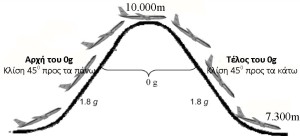
Κατά τη διάρκεια του παραβολικού πετάγματος το αεροπλάνο κινείται σε τροχιά που δίνει 0g (έλλειψη βαρύτητας) μέχρι 40 δευτερόλεπτα. Το παραβολικό πέταγμα δημιουργεί έλλειψη βαρύτητας ακολουθώντας μία τροχιά όπου η επιτάχυνση του αεροπλάνου εξουδετερώνει την επιτάχυνση της βαρύτητας (Εικ. 3) κατά μήκος του άξονα z, κάθετα προς τον αξονα του αεροπλάνου.
Εικ. 3. Σε πείσμα αυτού που πιστεύουν οι περισσότεροι, η φάση της μηδενικής επιτάχυνσης (0g, αιώρηση) της πτήσης αρχίζει όταν το αεροπλάνο ανεβαίνει και όχι όταν κατεβαίνει. Αν και το αεροπλάνο έχει ταχύτητα ανοδική, κατά τη διάρκεια της φάσης 0g, η επιτάχυνσή του έχει κατεύθυνση προς τα κάτω, πράγμα απαραίτητο, σύμφωνα με την εξίσωση (1), για να επιτευχθούν συνθήκες έλλειψης βαρύτητας.
Ειδικότερα, αν το αεροπλάνο και οι επιβάτες του επιταχυνθούν με την επιτάχυνση της βαρύτητας 
, έχουμε βάσει της εξίσωσης (1) μηδενική δύναμη αλληλεπίδρασης των επιβατών με το δάπεδο του αεροπλάνου, οπότε έτσι επιτυγχάνεται αιώρηση των επιβατών μέσα στο αεροπλάνο.
Μια τέτοιου είδους πτήση τυπικά αποτελείται από 30 έως 60 παραβολικές τροχιές, που η κάθε μία δίνει γύρω στα 25 δευτερόλεπτα αιώρηση. Μεταξύ των παραβολών το αεροπλάνο πρέπει να ανακτά ύψος, και μεταξύ αυτών των 40s χρονικών διαστημάτων, όπου η προς τα κάτω ταχύτητα μειώνεται και μετατρέπεται κατόπιν σε προς τα πάνω, η επιτάχυνση του αεροπλάνου φτάνει από g σε 1,8g.
Το πρόβλημα κατά την κίνηση σε παραβολική τροχιά είναι το πέταγμα να γίνεται κατά τέτοιο τρόπο ώστε οι επιβάτες να παραμένουν σε σταθερές θέσεις μέσα στο αεροπλάνο, παρόλο που αυτό παίρνει κλίσεις περίπου 
ως προς τη γη και κάνει περιστροφές στο άνω και κάτω μέρος της τροχιάς περίπου 
. Επομένως εκείνο που πρέπει να εξασφαλιστεί είναι να υπάρχει κατά μήκος του άξονα του αεροπλάνου και καθ’ όλη τη διάρκεια της πτήσης, συνισταμένη δυνάμεων πάνω στους επιβάτες ίση με μηδέν, ώστε να υπάρχει μόνο ένας βαθμός ελευθερίας στην κίνηση των επιβατών, κατά μήκος του άξονα z, κάθετα προς το δάπεδο του αεροπλάνου. Οι “κομήτες που ξερνάς” εξασφαλίζουν τις συνθήκες αυτές.
Γιάννης Γαϊσίδης
Πολύ καλό και “εύπεπτο” ακόμα και για μαθητές.Καλή συνέχεια αναμένουμε το επόμενο Γιάννη.