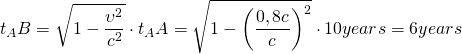Το Παράδοξο των Διδύμων

Το Παράδοξο των Διδύμων είναι ένα θέμα το οποίο μπορεί να εισαγάγει έναν ενδιαφερόμενο με σχετικά λίγες γνώσεις Φυσικής στις αρχές της ειδικής θεωρίας της σχετικότητας και να του κεντρίσει το ενδιαφέρον για τη γενική θεωρία της σχετικότητας, γιατί η επίλυση του προβλήματος περνάει και από μερικές εισαγωγικές έννοιες και αρχές της. Μια αρκετά κατανοητή ανάλυση παρουσιάζουμε εδώ, του Νορβηγού φυσικού του Πανεπιστημίου του Όσλο Øyvind Grøn, με μερικές δικές μου επεξηγήσεις για την καλύτερη κατανόηση από τους μη μυημένους.

Το πρόβλημα

Δύο δίδυμοι Α και Β συναντιούνται σε ένα μέρος. Κατόπιν απομακρύνεται ο ένας από τον άλλο και ξανασυναντιούνται αργότερα στο ίδιο μέρος. Ο δίδυμος Α θεωρεί ότι βρίσκεται σε ακινησία και προβλέπει ότι αδελφός του, όταν ξανασυναντηθούν, θα είναι νεότερος απ’ αυτόν λόγω της διαστολής του χρόνου που προβλέπει η σχετικότητα. Αλλά σύμφωνα με την αρχή της σχετικότητας, ο Β θεωρεί τον εαυτό του σε ακινησία ενώ ταξιδεύει ο Α, οπότε, όταν ξανασυναντηθούν, ο Α θα είναι νεότερος από τον Β. Αυτές ακριβώς οι αντικρουόμενες προβλέψεις είναι το Παράδοξο την Διδύμων.

Κάποιος μπορεί να δει ότι το παράδοξο αίρεται αμέσως αν σκεφτεί ότι προκειμένου να ξανασυναντηθούν – αναχώρηση, επιστροφή – τουλάχιστον ο ένας από τους δύο επιταχύνεται. Και η Ειδική Θεωρία της Σχετικότητας δεν ισχύει σε επιταχυνόμενες κινήσεις. Η επιτάχυνση είναι απόλυτη και όχι σχετική. Επομένως ο ένας από τους δύο δίδυμους δεν επιτρέπεται να θεωρήσει τον εαυτό του σε ημεμία. Ο δίδυμος με τη μεγαλύτερη μέση ταχύτητα, μεταξύ των δύο συναντήσεων, θα είναι νεότερος όταν ξανασυναντηθούν.

Το Παράδοξο των Δίδυμων μπορεί να αποτελέσει μια παιδαγωγική είσοδο στη Γενική Θεωρία της σχετικότητας. Όταν ο Αϊνστάιν παρουσίασε τη θεωρία αυτή το 1916 έγραψε στην εισαγωγή της ότι η Ειδική Θεωρία της Σχετικότητας περιέχει τον όρο “ειδική” για να εννοήσει. ότι οι αρχές της περιορίζονται στην κίνηση με σταθερή ταχύτητα.

Το Παράδοξο των Δίδυμων και η αρχή της σχετικότητας.

Φανταστείτε ότι ο δίδυμος Α παραμένει σε ηρεμία στη Γη και ο δίδυμος Β ταξιδεύει με ταχύτητα υ=0.8c (c είναι η ταχύτητα του φωτός, δηλαδή 300.000 km/s) προς το κοντινότερο άστρο Άλφα του Κενταύρου που βρίσκεται σε απόσταση 4 έτη φωτός (ε.φ) από τη Γη και γυρίζει πάλι πίσω στη Γη. Ως έτος φωτός ορίζουμε την απόσταση που είναι ίση με το διάστημα που διανύει το φως αν ταξιδέψει για ένα χρόνο. Σύμφωνα με τον Α το ταξίδι αυτό θα διαρκέσει:

(1) $\begin{equation*} t_AA=\frac{2L_0}{\upsilon}=\frac{2 \cdot 4 \epsilon. \phi } {0,8 \cdot c}=10years \end{equation*}$

Που σημαίνει ότι ο Α θα είναι γηραιότερος κατά 10χρόνια, όταν θα συναντάει ξανά το δίδυμο αδελφό του. Ο Α υπολόγισε ότι ο αδελφός του θα είναι κατά

(2) $\begin{equation*} t_AB=\sqrt{1- \frac{\upsilon^2}{c^2}} \cdot t_AA=\sqrt{1- \left( \frac{0,8c}{c} \right)^2} \cdot 10years=6years \end{equation*}$

πιο μεγάλος, κατα την επανένωσή τους.

Ορισμένες επεξηγήσεις

Στο σημείο αυτό είναι σκόπιμο να εξηγήσουμε ορισμένα σύμβολα και τύπους που χρησιμοποιήσαμε και θα χρησιμοποιήσουμε από δω και πέρα.

Με το σύμβολο t_AA εννοούμε το χρόνο του Α όπως τον υπολογίζει ο Α, δηλαδή ως προς το σύστημα αναφοράς του Α. Με το t_AB, το χρόνο του Β ως προς το σύστημα αναφοράς του Α, δηλαδή όπως τον υπολογίζει ο Α. Επομένως ο δείκτης (το μικρό γράμμα δίπλα στο σύμβολο) υπονοεί το σύστημα αναφοράς, δηλαδή ποιος κάνει τον υπολογισμό και το μεγάλο γράμμα δεξιά του δείχνει σε ποιον αφορά ο υπολογισμός. Π.χ. αν γράψουμε t_BA εννοούμε το χρόνο του Α, όπως τον υπολογίζει ο Β, δηλαδή ως προς το σύστημα αναφοράς του Β.

Ας κάνουμε και μία δεύτερη επισήμανση:

Ο τύπος:

$t=\frac{t_0}{\sqrt{1- \frac{\upsilon^2}{c^2}} }$

μας δίνει το χρόνο t, όπως τον αντιλαμβάνεται κάποιος που θεωρεί τον εαυτό του ακίνητο (δηλαδή με σύστημα αναφοράς τον εαυτό του) για κάποιον που κινείται με ταχύτητα υ ως προς αυτόν και μετράει χρόνο t₀κατά την κίνησή του. Αυτή είναι η λεγόμενη διαστολή του χρόνου γιατί δίνει πάντα χρόνο μεγαλύτερο από το χρόνο t₀ που μετράει αυτός που βρίσκεται σε κίνηση. Κάθε τύπος που περιέχει την έκφραση:

$\sqrt{1- \frac{\upsilon^2}{c^2}} }$

ονομάζεται μετασχηματισμός Lorrenz. Όπως είναι προφανές θα είναι πάντα μικρότερο του 1 γιατί οποιαδήποτε ταχύτητα σώματος είναι πάντα μικρότερη της ταχύτητας του φωτός. Δηλαδή υ < c.

Για το μήκος ισχύει ένας παρόμοιος τύπος, αλλά αυτή τη φορά έχουμε το γινόμενο::

(3) $\begin{equation*} L=L_0 \cdot \sqrt{1- \frac{\upsilon^2}{c^2}} \end{equation*}$

Επομένως για κάποιον που μετράει ένα μήκος θεωρώντας τον εαυτό του ακίνητο, θα το βρίσκει πιο μικρό από αυτό που μετράει ένας που ταξιδεύει με ταχύτητα υ. Αυτή είναι η λεγόμενη συστολή του μήκους.

Επανερχόμαστε στις σχέσεις (1) και (2).

Η (1) μας δίνει πόσο χρόνια θα έχει μετρήσει ο Α και η (2) πόσα ο Β, θεωρώντας τον Α ακίνητο (σύστημα αναφοράς). Ο Α θα μετρήσει 10 χρόνια και ο Β 6 χρόνια από τη στιγμή που έφυγε στο ταξίδι του ο Β μέχρι να γίνει η επανένωση των δύο αδελφών με την άφιξη του Β πίσω στη Γη.

Αλλά σύμφωνα με την ειδική θεωρία της σχετικότητας ο Β μπορεί να θεωρηθεί ακίνητος (σύστημα αναφοράς) και ότι ο Α κινείται. Τότε όμως ο Β θα έπρεπε να μετράει 10 χρόνια μέχρι την επανένωση και ο Α 6 χρόνια. Ιδού λοιπόν το παράδοξο των διδύμων.

Όμως η ειδική θεωρία της σχετικότητας δεν εφαρμόζεται στις επιταχυνόμενες κινήσεις. Στην περίπτωσή μας, όπου ο ένας των διδύμων απομακρύνεται και ξαναγυρίζει, τουλάχιστον στον ένα, υπάρχει επιτάχυνση κατα την αναχώρησή του. Επομένως χρειάζεται η γενική θεωρία της σχετικότητας.

Για το Β, θεωρώντας ότι εκείνος είναι ακίνητος και ότι κινείται ο Α, το μήκος της διαδρομής που εκτελεί ο Α θα είναι, σύμφωνα με τον τύπο (3)

$L=L_0 \cdot \sqrt{1- \frac{\upsilon^2}{c^2}}=4 \epsilon. \phi. \sqrt{1-\left( \frac{0,8c}{c} \right)^2}= 2,4 \epsilon. \phi.$

Σύμφωνα με τον Β ο χρόνος που περνάει γι αυτόν, όσο ο Α κάνει τη διαδρομή από τη Γη στον Άλφα του Κενταύρου και πίσω θα είναι:

(4) $\begin{equation*} t_BB=\frac{2L}{\upsilon}=\frac{2 \cdot 2,4 \epsilon.\phi.}{0,8c}=6years \end{equation*}$

Από τις σχέσεις (2) και (4) είναι φανερό ότι οι προβλέψεις του Α για το χρόνο του Β και οι προβλέψεις του Β για τον εαυτό του βρίσκονται σε συμφωνία. Δηλαδη t_AB=t_BB.

Ενώ λοιπόν για το χρόνο του Β υπάρχει συμφωνία για τα δύο συστήματα αναφοράς Α και Β, ας δούμε τι γίνεται για το χρόνο του Α, αν πάρουμε ως σύστημα αναφοράς το Β.

Για το χρόνο του Α , αφόσον κινείται, ως προς τον Β με ταχύτητα υ, θα ισχύει ο μετασχηματισμός Lorrenz για το χρόνο, όπου θα υπάρχει διαστολή του χρόνου του Β σε σχέση με το χρόνο του Α, επειδή το Α βρίσκεται σε κίνηση. Δηλαδή

$t_BB= \frac{t_BA}{\sqrt{1-\frac{\upsilon^2}{c^2}} }}$

Οπότε για το χρόνο του Α, ως προς σύστημα αναφοράς το Β θα έχουμε:

(5) $\begin{equation*} t_BA=\sqrt{1- \frac{\upsilon^2}{c^2}}} \cdot t_BB=0,6 \cdot 6=3,6years \end{equation*}$

Αυτό έρχεται σε αντίθεση με τα 10 χρόνια που υπολογίζει ο Α για τον εαυτό του. Δηλαδή, ενώ ο Α υπολογίζει χρονική διάρκεια 10 ετών μέχρι την επανένωση με τον αδελφό του, θεωρώντας ότι αυτός παραμένει ακίνητος και ο αδελφός του ταξιδεύει, ο Β υπολογίζει για τον Α 3,6 χρόνια, αν θεωρήσει ότι αυτός είναι ακίνητος και ταξιδεύει ο Α. Κάτι λοιπόν έχει χαθεί από τους υπολογισμούς του Β, όπως τους περιγράψαμε παραπάνω.

Ας δούμε από πιο κοντά τι συμβαίνει με τον Α, σύμφωνα με τον Β, όταν ο Β παίρνει τη στροφή και αρχίζει να γυρνάει από τον αστερισμό Άλφα του Κενταύρου. Όταν ο Β επιταχύνει προς τον αδελφό του υφίσταται την επίδραση ενός βαρυτικού πεδίου μακρυά από τον Α, ο οποίος είναι σε υψηλότερο βαρυτικό πεδίο από ό τι αυτός. Έτσι, ο Α στη Γη, όπως τον μετράει ο Β, γερνάει ταχύτερα από τον Β κατά το χρόνο επιτάχυνσής του:

(6) $\begin{equation*} \Delta t_BA= \frac{2 \upsilon}{g} \end{equation*}$

Για όσους έχουν λίγες γνώσεις επιπέδου λυκείου για την κατακόρυφη βολή προς τα πάνω, μπορούν να αναγνωρίσουν τον τύπο (5), όταν υπάρχει σταθερή επιτάχυνση βαρύτητας g. Θυμίζουμε ότι ως σύστημα αναφοράς εξακολουθούμε να διατηρούμε τον Β. Αν ο Β έχει κατάλληλη σταθερή επιτάχυνση g, από τη γενική θεωρία της σχετικότητας προκύπτει, ότι η σχέση μεταξύ του χρόνου του Α και του Β θα είναι:

$\Delta t_BA=\left( 1+\frac{g \cdot L_0}{c^2} \right) \cdot \Delta t_BB$

η οποία, με αντικατάσταση από την (5) δίνει:

(7) $\begin{equation*} \Delta t_BA=\left( 1+\frac{g \cdot L_0}{c^2} \right) \cdot\frac{2 \upsilon}{g}=\frac{2 \upsilon}{g}+\frac{2 \upsilon \cdot L_0}{c^2} \end{equation*}$

Όταν ό παραμένων στη Γη Α υπολόγισε το δικό του χρόνο και του Β κατά τη διάρκεια του ταξιδιού του Β, δεν έλαβε υπόψη του το χρόνο που προστέθηκε στον Α κατά τη στροφή του Β από τον Άλφα του Κενταύρου για να πάρει το δρόμο της επιστροφής. Θεώρησε δηλαδή ο Α ότι ο Β πήρε τη στροφή ακαριαία. Αυτό σημαίνει ότι ο χρόνος του είναι ορθός μόνο ύπό τον περιορισμό η επιτάχυνση της βαρύτητας g να τείνει προς το άπειρο, ώστε στη σχέςη (6) να μηδενίζεται ο χρόνος. Στην περίπτωση αυτή η (7) μας δίνει:

(8) $\begin{equation*} \Delta t_BA=\frac{2 \upsilon \cdot L_0}{c^2}=\frac{2 \cdot 0,8c \cdot 4 \epsilon. \phi.}{c^2}=6,4years \end{equation*}$

Επομένως ο συνολικός χρόνος του Α, όπως υπολογίζεται από τον Β, προκύπτει να προσθέσουμε τους δύο χρόνους από την (5) και την (8).

$t_BA+ \Delta t_BA=3,6+6,4=10years$

σε συμφωνία με την πρόβλεψη του Α για τον εαυτό του.

Άρα: Όταν οι δύο δίδυμοι θα ξανασυναντηθούν, όποιο σύστημα αναφοράς και να επιλέξουμε, είτε το Α είτε το Β, για μεν τον Α θα έχουν περάσει 10 χρόνια, για δε τον Β 6 χρόνια. Και αυτό συμβαίνει όταν ταξιδεύει ο ένας σε σχέση με τον άλλο με ταχύτητα το 80% της ταχύτητας του φωτός.

Όλη αυτή η ανάλυση θεωρήθηκε ότι έγινε στον επίπεδο χωρόχρονο και το συμπεράσμά μας είναι: ο δίδυμος που επιταχύνεται όταν βρίσκεται ο ένας μακρυά από τον άλλο, θα είναι νεότερος όταν ξανασυναντηθούν μετά το ταξίδι. Έχει αποδειχθεί ότι, αν και οι δύο επιταχύνονται, τότε αυτός που έχει τη μεγαλύτερη επιτάχυνση θα είναι και ο νεότερος της στιγμή της συνάντησης. Το ερώτημα αν καταλήγουμε στο ίδιο συμπέρασμα θεωρώντας το χωρόχρονο κυρτό και όχι επίπεδο, παραμένει, αλλά η απάντησή του ξεφεύγει από τα πλαίσια αυτής της ανάλυσης.

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr