To 1929 o Edwin Hubble, μετά από μακροχρόνιες παρατηρήσεις στο Αστεροσκοπείο του Όρους Ουίλσον, στην Καλιφόρνια, ανακοίνωσε ότι σε ένα σύμπαν που διαρκώς επεκτείνεται, όσο πιο μακρυά βρίσκεται ένας γαλαξίας από εμάς τόσο πιο γρήγορα κινείται. Βρήκε δηλαδή ότι οι ταχύτητες που απομακρύνονται οι γαλαξίες είναι ανάλογες της απόστασής τους από εμάς. Με την ανακάλυψη αυτή εδραιώθηκε η πεποίθηση στην επιστημονική κοινότητα ότι η θεωρία της Μεγάλης Έκρηξης είναι καλά τεκμηριωμένη.
Γιατί όμως συμβαίνει αυτό; Πώς επιβεβαιώνεται η θεωρία της Μεγάλης Έκρηξης με τα ευρήματα του Hubble;
Μια εξαιρετική προσέγγιση του πώς μπορούμε να βρούμε μία απλή και κατανοητή μέθοδο, την οποία να προτείνουμε στους μαθητές των μεγάλων τάξεων του λυκείου (Β΄ και Γ΄ τάξης) ή σε πρωτοετείς φοιτητές, περιγράφει ο Dr Ted Forringer, καθηγητής σε τεχνολογικό κολλέγιο της πολιτείας Georgia, ΗΠΑ, σε άρθρο του στο επιστημονικό περιοδικό The Physics Teacher με τίτλο “A Guided Innquiry on Hubble Plots and the Big Bang”.
O Dr Forringer χρησιμοποιεί απλά διαγράμματα, που δίνει στους μαθητές του, όπου φαίνονται οκτώ σωματίδια να κινούνται προς ορισμένες κατευθύνσεις και ζητάει από τους μαθητές να αναγνωρίσουν σε ποια από αυτά απεικονίζεται κάποια έκρηξη και με τι χαρακτηριστικά.
Αντί για τα διαγράμματα, με τη βοήθεια της εφαρμογής Interactive Physics, σχεδίασα τέσσερα μικρά βιντεάκια, με τα οποία μπορούμε να έχουμε μια άμεση παρουσιάση της όλης μεθόδου, αφήνοντας στον μαθητή να συνάγει τα συμπεράσματά του και να απαντήσει μόνος του στο ερώτημα, γιατί πιστεύουμε ότι το σύμπαν μας ξεκίνησε με μια έκρηξη δισεκατομμύρια χρόνια πριν.
Η φύση μιας έκρηξης
Η άσκηση ξεκινάει με την πιο βασική ιδέα: “Με τι θα έμοιαζε, αν παίρναμε μια φωτογραφία από μια ομάδα σωματιδίων που ξεκίνησε ως μέρος μιας ενιαίας έκρηξης;” Για τους σκοπούς αυτής της άσκησης, υποθέτουμε ότι, μετά την έκρηξη, τα σωματίδια θα κινούνται σε μια ευθεία γραμμή με σταθερή ταχύτητα. Υπάρχουν δύο κύρια κριτήρια για τον προσδιορισμό των ομάδων των σωματιδίων που παρήχθησαν σε έκρηξη:
Όλα τα σωματίδια πρέπει να απομακρύνονται από το ίδιο κεντρικό σημείο.
Δεδομένου ότι όλα τα σωματίδια ταξιδεύουν για το ίδιο χρονικό διάστημα, τα σωματίδια που είναι πιο μακριά πρέπει να κινούνται ταχύτερα. Αυτό συμβαίνει αν σκεφτούμε ότι 
. Επειδή τα σωματίδια παράχτηκαν την ίδια στιγμή, ο χρόνος t της κίνησής τους θα είναι κοινός για όλα. Όχι όμως και οι ταχύτητές τους, γιατί μετά από μία έκρηξη, όλα τα “θραύσματα” δε φεύγουν με την ίδια ταχύτητα. Επομένως αυτά που θα έχουν μεγαλύτερες ταχύτητες θα βρίσκονται και σε μεγαλύτερες αποστάσεις d.
Για την αντιμετώπιση του πρώτου σημείου, στους μαθητές εμφανίζονται τα δύο παρακάτω videos. Το video 1.1 , με σωματίδια που κινούνται μακριά από μια κεντρική θέση και το video 1.2, με όλα τα σωματίδια να κινούνται σε τυχαίες κατευθύνσεις. Ρωτούμε, ποιο αντιπροσωπεύει σωματίδια που θα μπορούσαν να προέρχονται από μια έκρηξη. Οι μαθητές το βρίσκουν αυτό απλό, και εύκολα αναγνωρίζουν ότι, προκειμένου να έχουν ξεκινήσει από μια έκρηξη, τα σωματίδια πρέπει να απομακρύνονται από μια κεντρική τοποθεσία
Στo επόμενο video όλα τα σωματίδια κινούνται σε τυχαίες κατευθύνσεις. Οι μαθητές πρέπει να είναι σε θέση να προσδιορίσουν ότι το πρώτο video παριστάνει σωματίδια που επεκτείνονται προς τα έξω μετά από μια έκρηξη, ενώ το δεύτερο δε δείχνει με σαφήνεια κάτι τέτοιο.
Το δεύτερο καθήκον είναι πιο δύσκολο. Στους μαθητές εμφανίζονται δύο άλλα videos, τα οποία δείχνουν σωματίδια που κινούνται μακριά από μια κεντρική θέση. Ωστόσο, στο ένα (video 2.1), τα σωματίδια που βρίσκονται μακρύτερα, κινούνται πιο γρήγορα, έτσι ώστε, εάν παρακολουθήσουν τα σωματίδια προς τα πίσω, οι μαθητές θα διαπιστώσουν ότι όλα ξεκίνησαν από το ίδιο μέρος την ίδια στιγμή (δηλαδή, η ταχύτητα είναι ανάλογη με την απόσταση). Στο δεύτερο (video 2.2) δεν υπάρχει συσχέτιση μεταξύ της απόστασης από την πηγή και της ταχύτητας, έτσι ώστε τα σωματίδια δεν θα μπορούσαν όλα να είχαν ξεκίνησει από το ίδιο μέρος την ίδια στιγμή.
Είναι εκπληκτικά δύσκολο να διακρίνει κανείς τις διαφορές σ’ αυτά τα videos απλά με ένα κοίταγμα. Πολλοί μαθητές στην αρχή πιθανόν να πιστέψουν ότι τα δύο videos δείχνουν τα αποτελέσματα μιας και μόνο έκρηξης.
Μαζί με κάθε video υπάρχουν τρεις πίνακες. Ο πρώτος δείχνει την απόσταση (location) κάθε σωματίδιου από την αρχή Ο σε m. Ο δεύτερος την ταχύτητα (velocity) κάθε σωματιδίου σε m/s. Χρησιμοποιώντας t = d / ν, οι μαθητές είναι σε θέση να καθορίσουν πόσο χρόνο χρειάζεται κάθε σωματίδιο να ταξιδέψει από την αρχή μέχρι την τρέχουσα θέση του. Ο τρίτος πίνακας δείχνει ακριβώς αυτούς τους χρόνους για το κάθε σωματίδιο.
Είναι πράγματι αρκετά δύσκολο οι μαθητές να καταλάβουν εξ αρχής ποιο από τα δύο videos, 2.1 και 2.2, αντιστοιχεί σε έκρηξη.
Για να τους διευκολύνουμε μπορούμε να ρωτήσουμε: “πριν από πόσο χρόνο κάθε σωματίδιο βρισκόταν στο αρχικό σημείο εκκίνησης;” Στο video που δείχνει το αποτέλεσμα μιας έκρηξης ο χρόνος θα είναι ο ίδιος για κάθε σωματίδιο. Σ’ αυτό που δε είναι αποτέλεμα έκρηξης προκύπτουν διαφορετικά χρονικά διαστήματα για κάθε σωματίδιο.
Κατασκευάζοντας το “διάγραμμα Hubble”
Το επόμενο βήμα είναι να δημιουργήσουν οι ίδιοι οι μαθητές το “διάγραμμα Hubble”.
Στο video 2.1 τα σωματίδια αρχίζουν την κίνησή τους όταν ήδη απέχουν από την αρχή της προέλευσής τους κατά 6s. Αν πάρουμε εκείνη τη στιγμή τις τιμές των αποστάσεων και των ταχυτήτων των σωματιδίων, όπως φαίνονται στο video πάνω αριστερά, μπορεί να κατασκευαστεί ένα “διάγραμμα Hubble” αποστάσεων-ταχυτήτων των σωματιδίων. Το διάγραμμα αυτό φαίνεται στην παρακάτω εικόνα 1.
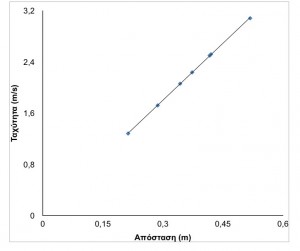
Εικ. 1. Διάγραμμα αποστάσεων-ταχυτήτων τη στιγμή 6s.. Ευθεία με σταθερή κλίση. Τι εκφράζει η κλίση αυτή;
Ζητείται από τους μαθητές να βρουν τη σχέση μεταξύ της κλίσης της γραφικής παράστασης και του χρόνου από τότε που σημειώθηκε η έκρηξη. Πρέπει να καταλάβουν ότι η κλίση του διαγράμματος Hubble είναι το αντίστροφο του χρόνου από την έκρηξη, 
. Αυτό είναι μια πρώτη εισαγωγή στη σταθερά Hubble H0.
Εφαρμογή στο σύμπαν μας
Το πραγματικό διάγραμμα Hubble είναι της εικόνας 2. Γρήγορα αναγνωρίζει κανείς ότι το διάγραμμα Hubble δείχνει κινούμενα αντικείμενα που είναι το αποτέλεσμα της έκρηξης (δηλαδή, μια ευθεία γραμμή).
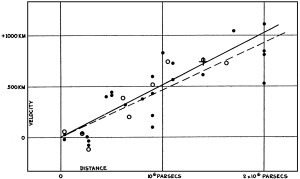
Εικ. 2. Το πραγματικό διάγραμμα Hubble. Στον οριζόντιο άξονα είναι οι αποστάσεις από τη Γη σε parsec και στον κατακόρυφο οι ταχύτητες των σουπερνόβα και των μεταβαλλόμενων Κηφίδων σε Km/s. Η κλίση της καλύτερα προσαρμοσμένης γραμμής δίνει την τιμή της σταθεράς του Hubble. Οι μαθητές είναι σε θέση να αναγνωρίσουν την «ευθεία γραμμή» του διαγράμματος και να συμφωνήσουν ότι τα σημεία των δεδομένων φαίνεται να αντιπροσωπεύουν μια έκρηξη που συνέβη περίπου 15 δισεκατομμύρια χρόνια πριν
Σύμφωνα με το νόμο του Hubble – οι ταχύτητες απομάκρυνσης των γαλαξιών είναι ανάλογες της απόστασής τους από μας – θα ισχύει 
, όπου Η0 η σταθερά Hubble. Συγκρίνοντας τη σχέση αυτή με την εξίσωση 
, είναι φανερό ότι η σταθρά Hubble έχει διαστάσεις [χρόνος]-1, δηλαδή αντίστροφες του χρόνου. Μπορεί επομένως κάποιος μετρώντας την κλίση της ευθείας στην εικ. 2 να βρει τη σταθερά Hubble, να την αντιστρέψει και, αν τη μετατρέψει σε χρόνια, μπορεί να υπολογίσει την ηλικία του σύμπαντος. Το χρόνο δηλαδή που μεσολάβησε από τη στιγμή της Μεγάλης Έκρηξης μέχρι σήμερα.
Είναι προφανές ότι η ακρίβεια του αποτελέματος εξαρτάται από την ακρίβεια των μετρήσεων που απεικονίζονται στο διάγραμμα της εικ. 2. Στο διάγραμμα αυτό η κλίση είναι Η0 =64km/s/Mpc (64Km/s ανά Μεγαπαρσέκ). Αυτό σημαίνει ότι η ταχύτητα απομάκρυνσης των γαλαξιών είναι 64 χιλιόμετρα ανά δευτερόλεπτο σε απόσταση 1 μεγαπαρσεκ. Σημειωτέον ότι το 1pc=3,26 έτη φωτός=3,09×1013 km). Για να το απλουστέψουμε: Σε κάθε 3,26 έτη φωτός απόσταση από μας, κάθε γαλαξιάς θα απομακρύνεται με ταχύτητα 64km/s. Με κατάλληλες μετατροπές των μονάδων και αντιστροφή της H0, βρίσκουμε ότι το σύμπαν άρχισε με μια έκρηξη, που συνέβη 15 δισεκατομμύρια χρόνια πριν, ένα αποτέλεσμα που αποκλίνει μόνο 9% από τις βέλτιστες τρέχουσες εκτιμήσεις της ηλικίας του σύμπαντος, 13,8 δισεκατομμύρια χρόνια.
Πρέπει όμως να γίνει αντιληπτό από τους μαθητές μας ότι με την εργασία αυτή, απλώς ανοίξαμε ένα κεφάλαιο, το οποίο αρχίζουν να το κατανοούν, γιατί έχουμε κάνει αρκετές απλουστεύσεις.
Είναι βέβαιο ότι θα εκλπαγούν όταν μάθουν ότι στο σύμπαν δεν υπάρχει επιβράδυνση στην επέκτασης του, όπως θα περίμενε κανείς λόγω της βαρυτικής έλξης. Στην πραγματικότητα όσο επεκτείνεται επιταχύνεται, μια πραγματικότητα που κέρδισε το βραβείο Νόμπελ 2011 στη Φυσική και έχει οδηγήσει στην ιδέα της “σκοτεινής ενέργειας”. Αυτό όμως είναι ένα άλλο ζήτημα.
Σημείιωση: Προς τιμήν του Edwin Hubble, δόθηκε το όνομά του στο δορυφορικό τηλεσκόπιο, το οποίο περιφέρεται γύρω από τον πλανήτη μας και μελετάει το σύμπαν, αναζητώντας νέους εξωπλανήτες που να μοιάζουν με τον πλανήτη μας. Μία από τις φωτογραφίες της κορυφής της βασικής σελίδας αυτού του site είναι η φωτογραφία του τηλεσκόπιου Hubble.
Θέλω να ευχαριστήσω το Dr Forringer για την άδειά του να μου επιτρέψει να κάνω αναφορά και να πάρω αρκετά σημεία από το άρθρο του, που μνημονέυω στην πρώτη παράγραφο του παρόντος άρθρου. Τα τέσσερα μικρά βιντεάκια του τα απέστειλα και θα τα δημοσιεύσει στο προσωπικό του site.
Γιάννης Γαϊσίδης
