Μετρήσεις Μήκους-Μέση Τιμή

Με κλικ εδώ κατέβασε μία σύντομη παρουσίαση σε Power Point της θεωρίας των μετρήσεων μήκους.

1. Αντιστοιχίστε τα φυσικά μεγέθη της αριστερής στήλης με τις μονάδες μέτρησής τους στη δεξιά. 

   Φυσικά μεγέθη			Μονάδες
   Χρόνος	Α	1	Χιλιόμετρα ανά ώρα(Km/h)
   Μήκος	Β	2	Μέτρο(m)
   Ταχύτητα	Γ	3	Βαθμοί Κελσίου (0C)
   Θερμοκρασία	Δ	4	Δευτερόλεπτα (s)

2. Ένας μαθητής μετράει το μήκος του θρανίου με τις πιθαμές του και το βρίσκει ίσο με 6,5 περίπου πιθαμές. Ο συμμαθητής του μετράει το ίδιο θρανίο και το βρίσκει 7 πιθαμές. Γιατί δε συμφωνούν στο αποτέλεσμα της μέτρησης; Τι πρέπει να κάνουν για να συμφωνήσουν;
3. Για να μετρήσει το πλάτος ενός δρόμου, ένας εργάτης χρησιμοποίησε μία ράβδο, που γνώριζε ότι είχε μήκος 1 μέτρο και 20 εκατοστά. Βρήκε ότι το πλάτος του δρόμου ήταν 12 ράβδοι και 1/4 της ράβδου. Πόσα μέτρα ήταν το πλάτος του δρόμου;
4. Ένας παγκόσμιος πρωταθλητής του μήκους υπολογίζει να κάνει 20 ακριβώς διασκελισμούς πριν φτάσει στη βαλβίβα εκτίναξης. Η απόστασή του από τη βαλβίδα πρέπει να είναι 42m, τη στιγμή που ξεκινάει. Πόσο θα είναι το μήκος του κάθε διασκελισμού του, αν υποθέσουμε ότι όλοι οι διασκελισμοί του είναι περίπου ίσοι;
5. Στην εικόνα φαίνεται ένα κοινό μέτρο, που χρησιμοποιούμε στην καθημερινότητά μας για να μετρούμε μήκη. Γιατί χρησιμοποιούμε το μέτρο για να μετρήσουμε μήκη και όχι π.χ το χρονόμετρο; Γιατί το μέτρο έχει το συγκεκριμένο μήκος και όχι μεγαλύτερο ή μικρότερο;
   

   Άσκηση 5

6. Τι ακρίβεια έχουμε με το μέτρο της προηγούμενη εικόνας; Εκατοστού, χιλιοστού, μέτρου ή άλλη;
7. Με το ίδιο μέτρο κάνουμε τέσσερις μετρήσεις, προσέχοντας να έχουμε όσο το δυνατόν μεγαλύτερη ακρίβεια. Σε ποια μέτρηση δεν είμαστε σίγουροι για την ακρίβεια του τελευταίου ψηφίου;
   1. 44cm
   2. 1,25m
   3. 45,4cm
   4. 62,73cm
8. Να γράψετε τα παρακάτω μήκη με ακρίβεια εκατοστού του μέτρου.
   1. 1,567m
   2. 2,242m
   3. 3,112m
   4. 4,999m
9. Να γράψετε τα παρακάτω μήκη με ακρίβεια χιλιοστού του μέτρου.
   1. 12,33cm
   2. 24,48cm
   3. 38,82cm
   4. 49,99cm
10. Πόσα εκατοστά είναι το μήκος του μικρού αντικειμένου της εικόνας; Δώστε όσο το δυνατόν ακριβέστερη τιμή. Ποια τιμή θα δίνατε αν σας ζητούσαν ακρίβεια χιλιοστού;
    

    Άσκηση 10

11. Ποια τιμή μήκους θα δίνατε για το μήκος του ίδιου μικρού αντικειμένου που μετρήσατε στην προηγούμενη άσκηση, αν χρησιμοποιούσατε τώρα το μέτρο της εικόνας; Βρίσκεις την ίδια τιμή με αυτή που είχες βρει; Γιατί;
    

    Άσκηση 11

12. Η διάμετρος της χάντρας είναι μεταξύ:
    

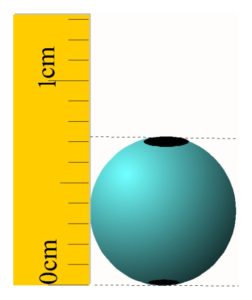
    Άσκηση 12

    1. 0cm και 1cm
    2. 0,5cm και 0,8cm
    3. 0,73cm και 0,74cm
    4. 0,7cm και 0,8cm
13. Πόσα εκατοστά, πόσα μέτρα και πόσα χιλιόμετρα είναι τα:
    1. 20mm
    2. 200mm
    3. 2.000mm
    4. 2.000.000mm
14. Ποιο από τα παρακάτω μήκη είναι ίσο με 2,35m;
    1. 0,235cm
    2. 23,5cm
    3. 235cm
    4. 2350cm
15. Κατατάξτε από το μικρότερο προς το μεγαλύτερο μήκος.
    1. 1,67m
    2. 16,7cm
    3. 16,7mm
    4. 1,67Km
16. Πόσα μέτρα (m) είναι τα:
    1. 56,3cm
    2. 435cm
    3. 546mm
    4. 2,34Km
17. Τέσσερις μαθητές μέτρησαν το μήκος του ίδιου μολυβιού και βρήκαν τις εξής τιμές:
    1. 18,34cm
    2. 18,31cm
    3. 18,36cm
    4. 18,33cm

    Ποια είναι η μέση τιμή των παραπάνω μετρήσεων; Πόσο αποκλίνει η τιμή που βρήκε ο κάθε μαθητής από τη μέση τιμή;

18. Μία ομάδα μαθητών μέτρησε το μήκος ενός θρανίου και βρήκε τις παρακάτω τιμές.

    A/A	Μήκος(cm)
    1	119,7
    2	119,6
    3	120,2
    4	119,9
    5	119,5
    6	119,9
    7	120,1
    8	120
    9	119,5
    10	120,3
    Άθροισμα:

    
    Υπολογίστε τη μέση τιμή των μηκών με προσέγγιση χιλιοστού του μέτρου (όπως είναι και οι τιμές του πίνακα). Ποια τιμή του πίνακα παρουσιάζει τη μεγαλύτερη απόκλιση από τη μέση τιμή;
19. Η μέση τιμή που προέκυψε από τις μετρήσεις ενός μήκους είναι 23,4cm. Η μέγιστη τιμή που πήραμε από τις μετρήσεις αποκλίνει 0,8cm και η ελάχιστη 0,6cm από τη μέση τιμή. Πόση είναι η μέγιστη τιμή και πόση η ελάχιστη που μετρήσαμε;
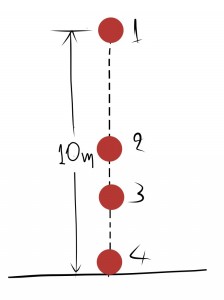
20. Αφήνουμε τη μικρή μπάλα να πέσει από ύψος 10m στο έδαφος (θέση 1). Σε κάθε αναπήδηση επί του εδάφους η μπάλα, λόγω απώλειας της ενέργειάς της, χάνει το 50% του ύψους της.
    1. Σε τι ύψος φτάνει η μπάλα μετά την πρώτη (θέση 2) αναπήδηση;
    2. Σε τι ύψος φτάνει μετά τη δεύτερη (θέση 3) αναπήδηση;
    3. Αν υποθέσουμε ότι μετά τη δεύτερη αναπήδηση η μπάλα σταματάει επί του εδάφους, πόσα μέτρα συνολικά κινήθηκε η μπάλα;
       

       Άσκηση 20

21. Γύρω από τον κύλινδρο είναι τυλιγμένο ένα νήμα, στην άκρη του οποίου είναι κρεμασμένο ένα σώμα Σ. Ο κύλινδρος μπορεί να περιστρέφεται γύρω από τον ακλόνητο άξονά του Κ. Αφήνουμε ελεύθερο το Σ να πέσει κρεμασμένο από το νήμα, οπότε ο κύλινδρος αρχίζει να περιστρέφεται. Πόσα μέτρα θα κατεβεί το Σ αν ο κύλινδρος κάνει 10 πλήρεις περιστροφές; Δίνεται η ακτίνα του κυλίνδρου R=10cm.
    

    Άσκηση 21

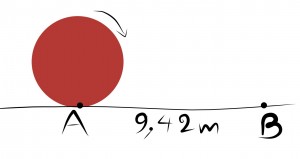
22. Η μπάλα της εικόνας περιστρέφεται 10 φορές για να κυλήσει από το σημείο Α μέχρι το Β διανύοντας 9,42m. Υπολογίστε τη διάμετρο της μπάλας.

Άσκηση 22

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr