Μερικές απλές μετρήσεις χαρακτηρίζουν εστίες διάδοσης, όπως το COVID-19, αλλά ο σωστός υπολογισμός τους είναι εκπληκτικά δύσκολος.
Από το Physics Today
Της Alison Hill
Η Alison Hill είναι επίκουρος καθηγήτρια στο Ινστιτούτο Υπολογιστικής Ιατρικής και στην ομάδα δυναμικής μολυσματικών ασθενειών στο Πανεπιστήμιο Johns Hopkins στη Βαλτιμόρη του Μέριλαντ. Είναι επίσης επισκέπτης μελετητής στο Πανεπιστήμιο του Χάρβαρντ στο Κέιμπριτζ της Μασαχουσέτης.
Το έτος 2020 έχει καθοριστεί από την πανδημία COVID-19: Ο νέος κοροναϊός, που είναι υπεύθυνος για αυτό, έχει μολύνει εκατομμύρια ανθρώπους και προκάλεσε περισσότερους από ένα εκατομμύριο θανάτους. Όπως τα HIV, Zika, Ebola και πολλά στελέχη της γρίπης, ο κοροναϊός έκανε το εξελικτικό άλμα από ζώα σε ανθρώπους προτού προκαλέσει εκτεταμένο χάος. Η μάχη για τον έλεγχο συνεχίζεται.
Όταν εντοπίζεται ένα ξέσπασμα ασθένειας – συνήθως μέσω μιας ανώμαλης όξυνσης σε περιπτώσεις με παρόμοια συμπτώματα – οι επιστήμονες σπεύδουν να κατανοήσουν τη νέα ασθένεια. Τι είδους μικρόβιο προκαλεί τη μόλυνση; Από πού προέρχεται; Πώς εξαπλώνεται η λοίμωξη; Ποια είναι τα συμπτώματά της; Ποια φάρμακα θα μπορούσαν να την αντιμετωπίσουν; Στην τρέχουσα επιδημία, η επιστήμη έχει προχωρήσει με φρενήρη ταχύτητα. Τα γονιδιώματα των ιών μπαίνουν σε μία αλληλουχία και αναλύονται γρήγορα, οι αριθμοί περιστατικών και θανάτων εμφανίζονται καθημερινά και εκατοντάδες προτυπωμένα στοιχεία κοινοποιούνται καθημερινά.
Μερικοί επιστήμονες σπεύδουν στα μικροσκόπια και τα εργαστήριά τους για να μελετήσουν μια νέα λοίμωξη. Άλλοι ορμούν στους υπολογιστές και στον κώδικα. Μερικές μετρήσεις μπορούν να χαρακτηρίσουν ένα νέο ξέσπασμα, να καθοδηγήσουν τις απαντήσεις στη δημόσια υγεία και να ενημερώσουν περίπλοκα μοντέλα που μπορούν να προβλέψουν την τροχιά της επιδημίας. Οι επιδημιολόγοι των λοιμώξεων, οι μαθηματικοί βιολόγοι, οι βιοστατιστικοί και άλλοι με παρόμοια εμπειρία προσπαθούν να απαντήσουν σε αρκετές ερωτήσεις: Πόσο γρήγορα εξαπλώνεται η λοίμωξη; Ποιο κλάσμα μετάδοσης πρέπει να μπλοκαριστεί για τον έλεγχο της εξάπλωσης; Πόσο καιρό είναι κάποιος μολυσματικός; Πόσο πιθανό είναι τα μολυσμένα άτομα να νοσηλευτούν ή να πεθάνουν;
Η φυσική θεωρείται συχνά η πιο μαθηματική επιστήμη, αλλά η θεωρία και η αυστηρή μαθηματική ανάλυση αποτελούν επίσης τη βάση της οικολογίας, της εξελικτικής βιολογίας και της επιδημιολογίας. Οι ιδέες και οι άνθρωποι ρέουν συνεχώς μεταξύ της φυσικής και αυτών των τομέων. Στην πραγματικότητα, η ιδέα της χρήσης μαθηματικών για την κατανόηση της εξάπλωσης μολυσματικών ασθενειών είναι παλαιότερη από την ίδια τη θεωρία των μικροβίων. Ο Daniel Bernoulli, διάσημος επιστήμονας ρευστομηχανικής, σχεδίασε ένα μοντέλο για να προβλέψει το όφελος των εμβολιασμών κατά της ευλογιάς το 1760, και ο βραβευμένος με Νόμπελ παθολόγος Ronald Ross δημιούργησε μαθηματικά μοντέλα για να ενθαρρύνει τον έλεγχο των κουνουπιών για τη μείωση της μετάδοσης της ελονοσίας. Μερικοί από τούς πιο παραγωγικούς δημιουργούς μοντέλων για την καταπολέμηση των επιδημιών σήμερα, αρχικά εκπαιδεύτηκαν ως φυσικοί, συμπεριλαμβανομένων του Neil Ferguson του Imperial College London, ενός συμβούλου της βρετανικής κυβέρνησης σχετικά με την αντιμετώπιση του COVID-19 και της Vittoria Colizza του Πανεπιστημίου Sorbonne στο Παρίσι, ηγέτιδος στη μοντελοποίηση της εξάπλωσης επιδημιών.
Αυτό το άρθρο παρουσιάζει τις βασικές μαθηματικές ποσότητες που χαρακτηρίζουν ένα ξέσπασμα επιδημίας, συνοψίζει τον τρόπο με τον οποίο οι επιστήμονες υπολογίζουν αυτούς τους αριθμούς και αποσαφηνίζει τις αποχρώσεις κατά την ερμηνεία τους. Για το COVID-19, οι εκτιμήσεις αυτών των ποσοτήτων κοινοποιούνται, συζητούνται και ενημερώνονται καθημερινά. Οι φυσικοί συνηθίζουν να αποστάζουν την πολυπλοκότητα του πραγματικού κόσμου σε ουσιαστικά, λιτά μοντέλα και μπορούν να χρησιμεύσουν ως σύμμαχοι στην επικοινωνία αυτών των ιδεών στο κοινό.
Δυναμική μετάδοσης
Λίγα επιστημονικά πεδία έχουν μία μόνο μέτρηση, για την οποία, τόσο οι εντός όσο και οι εκτός, έχουν εμμονή για τον βασικό αναπαραγωγικό αριθμό επιδημιολογίας των μολυσματικών ασθενειών, το R0 . Ο αριθμός, χωρίς μονάδα, ορίζεται ως ο μέσος όρος των νέων κρουσμάτων ή δευτερογενών λοιμώξεων, που προκαλούνται από ένα τυπικό μολυσμένο άτομο σε έναν πληττόμενο πληθυσμό. Είναι μία απλή ποσότητα που περιγράφει πόσο μολυσματικό είναι ένα δεδομένο παθογόνο και πόσο δύσκολο είναι να ελεγχθεί. (Δες παρακάτω το Πλαίσιο 1 για περισσότερα σχετικά με τον τρόπο ενσωμάτωσης των μοντέλων)
Πλαίσιο 1. Ποσοτικοποίηση της δυναμικής μετάδοσης
Ο βασικός αναπαραγωγικός αριθμός μιας ασθένειας R0 περιγράφει τον μέσο αριθμό δευτερογενών λοιμώξεων που δημιουργούνται από ένα μόνο μολυσμένο άτομο που εισάγεται σε έναν ευαίσθητο πληθυσμό. Για να απογειωθεί μια επιδημία, το R0 πρέπει να είναι μεγαλύτερο από 1. Η επιδημία θα τείνει να επιβραδύνεται, εάν το κλάσμα f του πληθυσμού που προστατεύεται από μόλυνση είναι αρκετά μεγάλο: f> 1−1 / R0.
Η διακύμανση των δευτερογενών λοιμώξεων μπορεί να είναι μεγάλη και μπορεί να οδηγήσει σε υπερδιαδεδομένα συμβάντα.Ο αριθμός των δευτερογενών λοιμώξεων συνοψίζεται συχνά από μια αρνητική διωνυμική κατανομή,
![]()
με τη μέση τιμή του R0, όπου k παραμετροποιεί τη διασπορά δευτερογενών λοιμώξεων, p = (1 + R0 / k)-1, και Γ είναι η συνάρτηση γάμμα. Εάν όλα τα άτομα έχουν την ίδια εγγενή μολυσματικότητα – δηλαδή, η διακύμανση είναι χαμηλή (μπλε σενάριο στα δεξιά) – τότε ο αριθμός των δευτερογενών λοιμώξεων αναμένεται να έχει κατανομή Poisson (k → ∞). Εάν η μολυσματικότητα είναι ετερογενής, η κατανομή λέμε ότι είναι υπερβολικά διασπαρμένη και έχει χαμηλότερο k. Η υπερβολική διασπορά συνεπάγεται ότι ένας μικρός αριθμός ατόμων είναι υπεύθυνοι για ένα μεγάλο ποσοστό δευτερογενών λοιμώξεων (διακεκομμένες γραμμές), ενώ οι περισσότεροι άλλοι δεν μολύνουν κανέναν, γεγονός που προκαλεί εξαφάνιση των αλυσίδων μόλυνσης. Για το COVID-19, μερικές μελέτες έχουν εκτιμήσει k≈0,5 (κίτρινο στα δεξιά), αν και με υψηλή αβεβαιότητα.
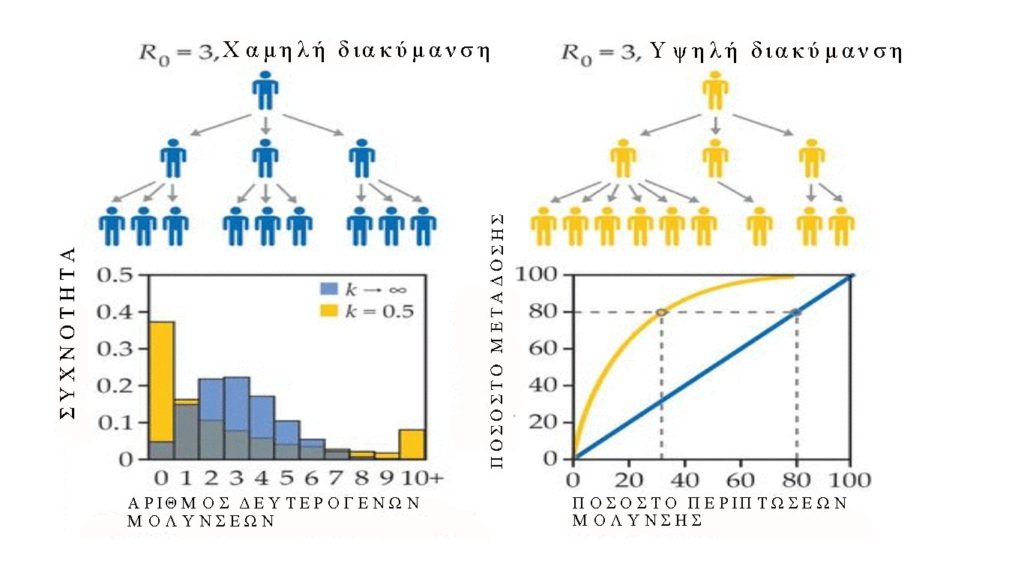
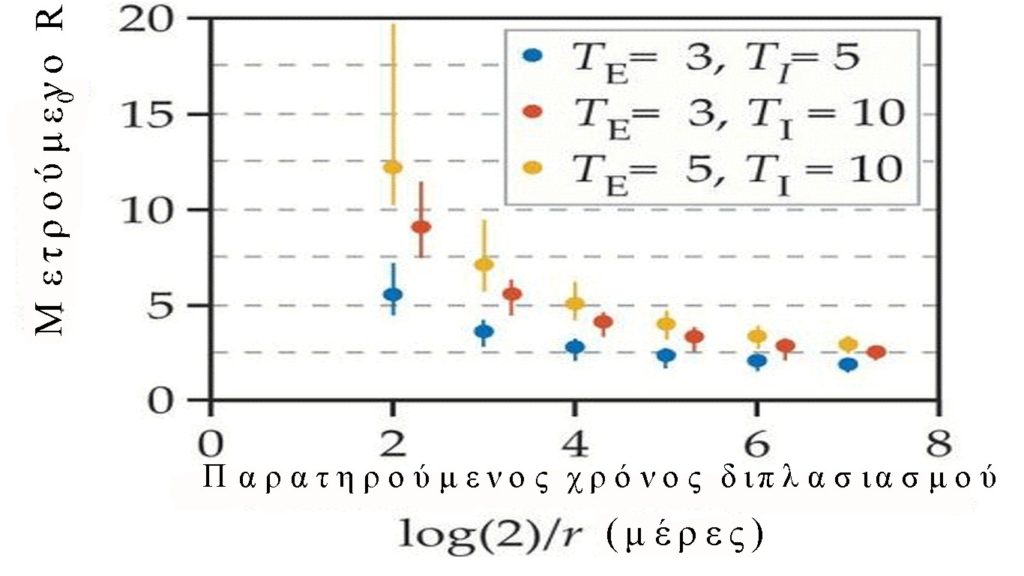
Η άμεση εκτίμηση του R0 είναι δύσκολη. Αντίθετα, η τιμή της προκύπτει συνήθως από τον εκθετικό ρυθμό ανάπτυξης της νόσου στις αρχές της επιδημίας και από την κλίμακα χρόνου της λοίμωξης(εικόνα 2). Για παράδειγμα, εάν είναι γνωστή η μέση διάρκεια των λανθανουσών και μολυσματικών περιόδων (TE και TI, αντίστοιχα) και υποθέσουμε ότι οι περίοδοι έχουν εκθετικές κατανομές, τότε R0 = (1 + rTE) (1 + rTI) (τελείες στο κάτω μέρος της γραφική παράσταση). Άλλα σχήματα διανομής οδηγούν σε διαφορετικές εκτιμήσεις για το R0 (γραμμές σφάλματος). Οι ρυθμοί ανάπτυξης επιδημίας σε επίπεδο χώρας που κυμαίνονται από 0,1-0,4 ανά ημέρα, έχουν παρατηρηθεί για το COVID-19, ο οποίος αντιστοιχεί σε χρόνους διπλασιασμού των 2-8 ημερών. Οι εκτιμήσεις του R0 ήταν γενικά μεταξύ 2 και 3, αν και μερικές φορές είναι πολύ υψηλότερες ανάλογα με τη ρύθμιση που παρατηρήθηκε και τις παραδοχές σχετικά με τα διαστήματα μετάδοσης.
Η δυναμική των μολυσματικών ασθενειών εμφανίζει σχεδόν πάντα κρίσιμη συμπεριφορά ή συμπεριφορά κατωφλίου, με την οποία η εξάπλωση απογειώνεται μόνο υπό ορισμένες συνθήκες. Ελλείψει αυτών των συνθηκών, η εξάπλωση εξασθενεί, όπως συμβαίνει σε μια αλυσίδα πυρηνικών αντιδράσεων. Η τιμή του R0 καθορίζει το αποτέλεσμα που προκύπτει. Εάν η εξάπλωση της νόσου διαμορφώνεται με συνεχείς διαφορικές εξισώσεις, το R0 βοηθά στον προσδιορισμό πότε μια κατάσταση ισορροπίας είναι σταθερή ή ασταθής. Αν η εξάπλωση καταγράφεται ως σειρά στοχαστικών αντιδράσεων, το R0 καθορίζει εάν η εξαφάνιση ή η εγκατάσταση είναι πιο πιθανή.
Χοντρικά, το R0 εξαρτάται από το γινόμενο τριών παραγόντων: το ποσοστό επαφής ή τον αριθμό των ατόμων που αλληλεπιδρά με ένα μολυσμένο άτομο κάθε μέρα, τη δυνατότητα μετάδοσης ή την πιθανότητα ανά μονάδα χρόνου, που οποιαδήποτε δεδομένη επαφή έχει ως αποτέλεσμα τη μετάδοση, και τη διάρκεια της μόλυνσης. Ο στόχος των περισσότερων προσπαθειών ελέγχου των λοιμωδών νόσων είναι η μείωση του R0 αλλάζοντας έναν ή περισσότερους από αυτούς τους παράγοντες. Για παράδειγμα, το ποσοστό επαφής μπορεί να μειωθεί περιορίζοντας τις συνδέσεις ενός μολυσμένου ατόμου μέσω γενικής κοινωνικής απόστασης ή στοχευμένης απομόνωσης. Η μεταδοτικότητα μπορεί να μειωθεί περιορίζοντας την πιθανότητα μόλυνσης κατά τη διάρκεια κάθε αλληλεπίδρασης μέσω κατάλληλων μέτρων όπως η χρήση μάσκας. Η διάρκεια μιας λοίμωξης μπορεί συχνά να μειωθεί με θεραπείες εκκαθάρισης μικροβίων, όπως αντιβιοτικά για τον στρεπτόκοκκο, αλλά τέτοια φάρμακα δεν είναι ακόμη διαθέσιμα για το COVID-19. Ένας άλλος τρόπος μείωσης του R0 είναι να μειωθεί ο αριθμός των ευπαθών ατόμων, κάτι που θα μπορούσε τελικά να κάνει ένα εμβόλιο.
Ως μετρήσιμο μέγεθος, το R0 έχει πολλούς σημαντικούς περιορισμούς. Δεν λέει τίποτα για τη μολυσματικότητα μιας ασθένειας, η οποία χαρακτηρίζει το πόσο θανατηφόρα είναι. Λοιμώξεις με μικρές τιμές R0, όπως το SARS (σοβαρό οξύ αναπνευστικό σύνδρομο), μπορεί να είναι εξαιρετικά θανατηφόρες. Άλλες με υψηλές τιμές, όπως ανεμοβλογιά, σπάνια οδηγούν σε θάνατο. Ορισμένες λοιμώξεις, όπως η ευλογιά, έχουν υψηλό R0 όσο και υψηλό κίνδυνο θανάτου. Επίσης, το R0 δεν αντικατοπτρίζει τη χρονική κλίμακα κατά την οποία εξαπλώνεται μια ασθένεια. Ο μέσος αριθμός νέων περιπτώσεων που περιγράφονται από τον R0 μπορεί να συμβεί μέσα σε λίγες ημέρες, όπως με το κοινό κρυολόγημα, ή πολλά χρόνια, κάτι που είναι χαρακτηριστικό για τον ιό HIV.
Σε αντίθεση με τη δημοφιλή πεποίθηση, το R0 δεν είναι εγγενής ιδιότητα μιας λοίμωξης περισσότερο από ότι ο αριθμός Reynolds για ένα υγρό. Εξαρτάται σε μεγάλο βαθμό από τον πληθυσμό στον οποίο εξαπλώνεται μια ασθένεια. Η ίδια μόλυνση θα μπορούσε να έχει υψηλό R0 σε πυκνό πληθυσμό με κακή υγιεινή και ανοσοποιητικά συστήματα εξασθενημένα από υποσιτισμό, αλλά πολύ χαμηλότερη αξία σε έναν πληθυσμό με καλύτερες συνθήκες διαβίωσης και γενική υγεία. Ακόμη και δημογραφικές λεπτομέρειες, όπως το ποσοστό των ατόμων σε ομάδες υψηλού κινδύνου ή τα πρότυπα κοινωνικής ανάμειξης, μπορούν να επηρεάσουν το R0 . Ο μέσος αριθμός δευτερογενών λοιμώξεων μπορεί επίσης να αλλάξει δραματικά κατά τη διάρκεια μιας επιδημίας και αντικατοπτρίζεται στον αποτελεσματικό αριθμό αναπαραγωγής, ο οποίος προσαρμόζεται καθώς τα άτομα αλλάζουν τη συμπεριφορά τους για να αποφύγουν τη μόλυνση.
Παρά τους περιορισμούς, η γνώση του αναπαραγωγικού αριθμού μιας ασθένειας εξακολουθεί να είναι χρήσιμη σε μία διάδοση. Για παράδειγμα, οι Stephen Kissler και Christine Tedijanto στο Πανεπιστήμιο του Χάρβαρντ βρήκαν ότι με εκτιμώμενο R0 στο 2,2, οι άνθρωποι στις ΗΠΑ θα πρέπει να μειώσουν τις επαφές τους κατά 60% μέσω της κοινωνικής απόστασης για τουλάχιστον στο 70% της επιδημίας, για να αποφύγουν την υπερχείλιση της φέρουσας ικανότητας των μονάδων εντατικής θεραπείας. Η Luca Ferretti και ο Chris Wymant στο Πανεπιστήμιο της Οξφόρδης υπολόγισαν κατ’ εκτίμηση για R0 = 2,0, ο έλεγχος και η ανίχνευση επαφών θα μπορούσαν να ελέγξουν την επιδημία μόνο εάν το 75% των επιβεβαιωμένων και ύποπτων περιπτώσεων απομονωθούν εντός δύο ημερών.
Μετά από εκτίμηση του R0 = 5,7 στην αρχή της διάδοσης της λοίμωξης στο Wuhan της Κίνας, οι Steven Sanche και Yen Ting Lin στο Εθνικό Εργαστήριο του Los Alamos, υπολόγισαν ότι ο έλεγχος θα απαιτούσε την απομόνωση του 50% των μολυσμένων ατόμων, καθώς και μείωση κατά 50% σε όλες τις επαφές μέσω κοινωνικής απόστασης. Ο Huaiyu Tian στο Πανεπιστήμιο Normal του Πεκίνου και οι συνάδελφοί του εκτίμησαν ότι στις αρχές της επιδημίας το R0 ήταν, κατά μέσο όρο, 3,1 στις κινεζικές πόλεις, αλλά μειώθηκε γρήγορα σε περίπου 1 σε πόλεις που εφάρμοσαν ταχέως μέτρα ελέγχου και μειώθηκαν περαιτέρω σε περίπου 0,04 υπό πιο έντονους ελέγχους.
Αλλά από πού προέρχονταν αυτές οι τιμές του R0; Η εκτίμηση του R0 είναι εξαιρετικά δύσκολη. Σπάνια παρατηρείται μια πλήρης αλυσίδα συμβάντων μετάδοσης που ξεκινά από ένα άτομο. Αυτό είναι συχνά δυνατό μόνο όταν η λοίμωξη είναι ακόμη σχετικά σπάνια, τα συμπτώματα είναι σχετικά μοναδικά, υπάρχουν διαθέσιμες καλές διαγνωστικές εξετάσεις και μπορεί να γίνει δειγματοληψία υψηλού ποσοστού του πληθυσμού (βλ. Εικόνα 1). Σε μελέτες ανίχνευσης επαφής, μόλις διαγνωστεί ένα άτομο, οι επαγγελματίες της δημόσιας υγείας εντοπίζουν οποιονδήποτε μπορεί να έχει επικοινωνήσει με αυτό το άτομο κατά τη διάρκεια της μολυσματικής περιόδου του και να τον ελέγξουν για την ασθένεια. Οι ερευνητές χρησιμοποιούν τα δεδομένα για να εκτιμήσουν το R0 για μία μόνο γενιά λοίμωξης.

Ωστόσο, άμεσες εκτιμήσεις του R0 μπορούν να γίνουν εκ των προτέρων. Για παράδειγμα, τα κρούσματα είναι πιο πιθανό να εντοπιστούν, όταν πολλά άτομα μολύνθηκαν από μία μόνο πηγή – συμβάν υπερδιάδοσης – οπότε οι εκτιμήσεις θα μπορούσαν να είναι μεροληπτικές προς τα πάνω. Εναλλακτικά, τα άτομα που μελετώνται μπορεί να είναι πιο πιθανό να διαγνωστούν από το μέσο άτομο και να απομονωθούν γρήγορα, οδηγώντας σε υποτιμήσεις του πραγματικού R0 .
Οι έμμεσες εκτιμήσεις είναι επομένως πιο συχνές και μπορεί να δώσουν πιο αντιπροσωπευτικές τιμές. Ένας κοινός τρόπος έμμεσης εκτίμησης του R0 περιλαμβάνει την παρακολούθηση του ρυθμού ανάπτυξης μιας επιδημίας. Από μόνο του το R0 δεν καθορίζει πόσο γρήγορα εξαπλώνεται μια ασθένεια. Εξαρτάται επίσης από τη χρονική κλίμακα κατά την οποία εμφανίζονται οι δευτερογενείς λοιμώξεις ενός ατόμου. Ωστόσο, εάν μπορεί να προσδιοριστεί ο μέσος χρόνος ενός ατόμου που είναι μολυσματικός, τότε είναι γενικά δυνατό, με κάποια μαθηματικά κόλπα, να εκτιμηθεί το R0 ενός πληθυσμού από τον ρυθμό εξάπλωσης της νόσου. (Δες Πλαίσιο 1)
Χρονική κλίμακα μόλυνσης
Η εκθετική αύξηση του αριθμού των λοιμώξεων είναι καθοριστικό χαρακτηριστικό των επιδημιών στην αρχή της πορείας τους. Εκτιμήσεις του ρυθμού ανάπτυξης r , ή, εναλλακτικά, του χρόνου διπλασιασμού Τ2 = log (2) / r , μπορούν να μας δώσουν βραχυπρόθεσμες προβλέψεις για την επιδημία.
Όπως το R0 , το r δεν είναι εγγενής ιδιότητα μιας λοίμωξης: ποικίλλει μεταξύ περιοχών και με την πάροδο του χρόνου. Συνήθως, η μεταβολή στο r εμφανίζεται για τους ίδιους λόγους όπως στο R0, όπως αλλαγές στην ανθρώπινη συμπεριφορά, που μειώνουν την εξάπλωση. Αλλά οι εκτιμήσεις του r υπόκεινται επίσης σε άλλους παράγοντες. Δραματικές αλλαγές στην δυνατότητα των τεστ, που αλλάζουν το ποσοστό των περιπτώσεων που εντοπίστηκαν και αναφέρθηκαν, μπορούν να οδηγήσουν σε μεροληπτικές εκτιμήσεις του r , όπως και αλλαγές στις καθυστερήσεις αναφορών.
Παρατηρούμενοι εκθετικοί ρυθμοί ανάπτυξης μπορούν να χρησιμοποιηθούν για τη στήριξη του R0 , το οποίο έχει μια πιο διαισθητική ερμηνεία και συνδέεται πιο άμεσα με την υποκείμενη διαδικασία μετάδοσης ασθενειών. Οι ερευνητές έχουν εξαγάγει μαθηματικές εξισώσεις για να συσχετίσουν το r με το R0 υπό διαφορετικές παραδοχές σχετικά με τη μετάδοση. (Δες Πλαίσιο 1). Σε γενικές γραμμές, αυτοί οι τύποι απαιτούν να γνωρίζουμε πόσο καιρό ένα τυπικό άτομο είναι μολυσματικό και την καθυστέρηση μεταξύ του πότε κάποιος μολύνεται και πότε γίνεται μολυσματικός, γνωστός ως λανθάνουσα περίοδος (βλ. Εικόνα 2). Ένας υψηλός παρατηρημένος εκθετικός ρυθμός ανάπτυξης της λοίμωξης συνεπάγεται υψηλό R0 εάν είτε η λανθάνουσα περίοδος είτε η μολυσματική περίοδος είναι μεγάλη, ενώ θα μπορούσε να σημαίνει πολύ μικρότερη τιμή εάν και τα δύο αυτά διαστήματα είναι μικρά.

Οι λανθάνουσες και μολυσματικές περίοδοι μιας νόσου μπορούν να εκτιμηθούν ακολουθώντας μεμονωμένους ασθενείς με γνωστές ημερομηνίες έκθεσης σε λοίμωξη. Χρειάζεται όμως κάτι παραπάνω από τη μέση διάρκεια των διαστημάτων για να προσδιοριστεί η σχέση μεταξύ του r και του R0 : Αρκετοί ασθενείς πρέπει να μελετηθούν για να πάρουμε μια λογική εκτίμηση της πλήρους κατανομής. Για πολλές μολύνσεις, οι λανθάνουσες και μολυσματικές περίοδοι αναγνωρίζονται εύκολα επειδή αντιστοιχούν σε συμπτώματα ασθένειας. Ωστόσο, για το COVID-19 αυτό δεν συμβαίνει: Τα άτομα συχνά ρίχνουν τον ιό στις αναπνευστικές εκκρίσεις τους και είναι πολύ μολυσματικά πριν εμφανίσουν συμπτώματα, όπως βήχα ή πυρετό. Η περίοδος επώασης – ο χρόνος έως ότου αναπτυχθούν τα συμπτώματα – είναι επομένως γενικά μεγαλύτερος από την λανθάνουσα περίοδο (βλ. Εικόνα 2). Επιπλέον, φαίνεται ότι πολλά από τα συμπτώματα του COVID-19 εκτείνονται πολύ πέρα από τη μολυσματική περίοδο. Επομένως, απαιτούνται επιδημιολογικές πληροφορίες και όχι παρακολούθηση συμπτωμάτων για να εκτιμηθεί πότε κάποιος ήταν μολυσματικός.
Οι επιδημιολόγοι των μολυσματικών ασθενειών συχνά χρησιμοποιούν τις παρατηρούμενες αλυσίδες μετάδοσης για να προσδιορίσουν το χρονοδιάγραμμα της μολυσματικότητας σε σχέση με την πορεία της νόσου. Το κάνουν με την εκτίμηση είτε του διαστήματος παραγωγής, του χρόνου μεταξύ του οποίου μολύνθηκε ένα άτομο και μόλυνε μια δευτερεύουσα περίπτωση, είτε του διαστήματος συρροής μεταξύ του χρόνου της έναρξης των συμπτωμάτων στο πρώτο άτομο και στο άτομο που μολύνθηκε δευτερογενώς ( βλέπε Εικόνα 2). Η μέτρηση του διαστήματος συρροής είναι πιο συνηθισμένη επειδή η εμφάνιση των συμπτωμάτων είναι γενικά πιο εύκολο να διακριθεί από τον χρόνο μόλυνσης.
Το διάστημα συρροής είναι μια μαθηματική συνάρτηση της περιόδου επώασης και των μολυσματικών περιόδων, οπότε αν το ένα είναι γνωστό, το άλλο μπορεί να υπολογιστεί. Οι ερευνητές έχουν αναπτύξει τύπους που σχετίζουν άμεσα την κατανομή διαστημάτων συρροής με το r και R0 χωρίς την πρώτη ανάκτηση των μεμονωμένων περιόδων. Αυτοί οι τύποι έχουν γίνει ο πιο συνηθισμένος τρόπος εκτίμησης του R0. Ωστόσο οι υπολογισμένες τιμές του R0 υπόκεινται σε σφάλματα στις εκτιμήσεις του διαστήματος συρροής. Για παράδειγμα, τα άτομα που εγγράφονται σε ερευνητικές μελέτες είναι συχνά απομονωμένα λίγο μετά τη διάγνωση, γεγονός που μειώνει το χρόνο που πρέπει να μολύνουν άλλους.
Η εκτίμηση της διάρκειας των σταδίων μόλυνσης παρέχει πληροφορίες για έλεγχο της επιδημίας πέραν του R0. Η κατανομή των μολυσματικών περιόδων καθορίζει το πόσο καιρό τα μολυσμένα άτομα πρέπει να απομονωθούν για να αποτρέψουν τη μόλυνση άλλων.
Πόσο θανατηφόρα είναι;
Μέχρι στιγμής έχουμε χαρακτηρίσει επιδημίες χρησιμοποιώντας: τη βασική αναπαραγωγική αναλογία R0 , η οποία συνοψίζει το δυναμικό μετάδοσης ενός μολυσμένου ατόμου, τον εκθετικό ρυθμό ανάπτυξης r, ο οποίος αποκαλύπτει πόσο γρήγορα αυξάνεται η επιδημία και τα χρονικά διαστήματα μόλυνσης, τα οποία καταγράφουν πώς η πορεία της νόσου σε ένα άτομο καθορίζει τη χρονική κλίμακα της μόλυνσης σε επίπεδο πληθυσμού. Αλλά αυτές οι μετρήσεις χάνουν ένα βασικό χαρακτηριστικό: πόσο θανατηφόρα είναι η ασθένεια.
Η θνησιμότητα μιας μολυσματικής ασθένειας ορίζεται συνήθως ως η πιθανότητα ότι ένα μολυσμένο άτομο θα πεθάνει τελικά από την ασθένεια και συνήθως αναφέρεται ως κίνδυνος θνησιμότητας (Case Fatality Risk, CFR, δες Πλαίσιο 2). Το CFR για το COVID-19 έχει συζητηθεί έντονα, και παρόλο που οι επιστήμονες έχουν συγκλίνει γενικά σε μια εκτίμηση περίπου στο 1%, οι ερευνητές, ο τύπος και το ευρύ κοινό συνεχίζουν να εξετάζουν αυτήν την τιμή. Μερικοί επιμένουν ότι το COVID-19 είναι «απλώς μια άλλη γρίπη», ενώ άλλοι παρουσιάζουν υπερβολικά στοιχεία για συνολικούς θανάτους που υπερβαίνουν κατά πολύ τις επίσημες αναφορές. Για να κατανοήσουμε τις αντιπαραθέσεις, είναι σημαντικό να κατανοήσουμε τις επιπλοκές στην εκτίμηση του CFR.
Πλαίσιο 2. Εκτίμηση του κινδύνου θανάτου κατά τη διάρκεια μιας επιδημίας
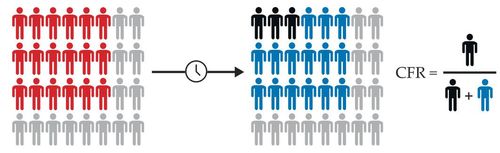
Οι επιδημιολόγοι χρησιμοποιούν τον κίνδυνο θνησιμότητας περιστατικών μιας νόσου (CFR) για να περιγράψουν το ποσοστό των ατόμων που επιβεβαιώθηκαν ότι έχουν μολυνθεί (κόκκινο, πάνω δεξιά) που τελικά θα πεθάνουν από την ασθένεια (μαύρο) αντί να ανακάμψουν (μπλε) Το πραγματικό CFR μπορεί να προσδιοριστεί με ακρίβεια μόνο ακολουθώντας μια ομάδα μολυσμένων ατόμων έως ότου παρατηρηθεί το τελικό αποτέλεσμα.
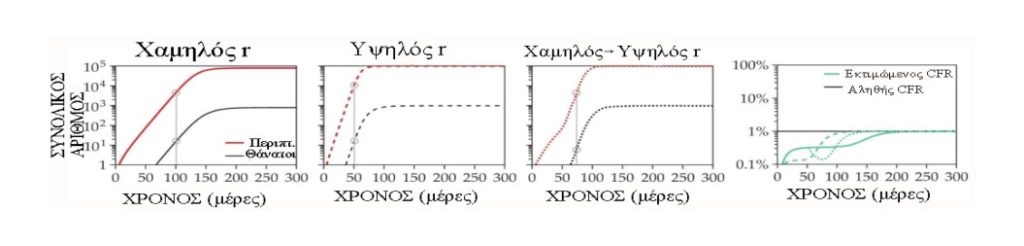
Η αναλογία του αριθμού των θανάτων που παρατηρήθηκαν έως ένα συγκεκριμένο χρονικό διάστημα με τον αριθμό των περιπτώσεων που αναφέρθηκαν έως την ίδια ημέρα (γκρίζοι κύκλοι στα παρακάτω γραφήματα) μπορεί να δώσει μια εσφαλμένη εκτίμηση του πραγματικού κινδύνου θανάτου. Η εκτίμηση του κινδύνου είναι ιδιαίτερα στρεβλωμένη όταν η επιδημία έχει υψηλό εκθετικό ρυθμό ανάπτυξης r, όταν το r αλλάζει γρήγορα και όταν υπάρχει μεγάλη καθυστέρηση μεταξύ μόλυνσης και θανάτου. Αυτό συμβαίνει επειδή το σύνολο των περιπτώσεων από τα οποία προήλθαν οι παρατηρούμενοι θάνατοι σημειώθηκαν στο παρελθόν, όταν η επιδημία ήταν μικρότερη.
Στο απλό μοντέλο μόλυνσης που εμφανίζεται εδώ, τα άτομα είναι μολυσματικά μόνο για περίπου πέντε ημέρες, αλλά μπορεί να χρειαστούν επιπλέον δύο εβδομάδες για να πεθάνουν. Το αληθινό CFR είναι 1%, το οποίο υποτιμάται δραματικά από την αναλογία θανάτων προς κρούσματα στις αρχές της επιδημίας (σωστό γράφημα). Σε πραγματικά δεδομένα, η αναλογία μπορεί περαιτέρω να συγχέεται με την υποβολή αναφορών ή την καθυστέρηση αναφοράς.
Μια σημείωση για την ορολογία: Η συντομογραφία CFR προκαλεί σύγχυση επειδή το R μπορεί να αντισταθμίσει το ρυθμό, την αναλογία και τον κίνδυνο. Στην επιδημιολογία, οι τρεις λέξεις έχουν ακριβείς σημασίες. Ο ρυθμός συνεπάγεται γενικά μια μονάδα αντίστροφου χρόνου και σπάνια χρησιμοποιείται για να περιγράψει μια βραχυπρόθεσμη λοίμωξη που επηρεάζει μόνο ένα μέρος του πληθυσμού. Η αναλογία συγκρίνει δύο διαφορετικούς πληθυσμούς. Μόνο μια μέτρηση κινδύνου περιγράφει μια αναλογία στην οποία τα άτομα που υπολογίζονται στον αριθμητή είναι ένα υποσύνολο εκείνων του παρονομαστή. Αυτό είναι που χρειάζεται για να μετρηθεί η πιθανότητα θανάτου ενός μολυσμένου ατόμου.
Ένα κοινό λάθος στην εκτίμηση του CFR μιας ασθένειας είναι απλώς να διαιρέσετε το συνολικό αριθμό των θανάτων που συνέβησαν μέχρι μια συγκεκριμένη ημέρα με τον σωρευτικό αριθμό των περιπτώσεων που διαγνώστηκαν μέχρι την ίδια ημέρα. Αυτός ο λόγος είναι μία εσφαλμένη εκτίμηση της πιθανότητας θανάτου λόγω λοίμωξης, ειδικά κατά τη διάρκεια μιας ταχέως αναπτυσσόμενης επιδημίας. (Δες το πλαίσιο 2 για ένα απλό μοντέλο που δείχνει αυτό το σημείο). Για να προσδιοριστεί σωστά ο κίνδυνος θανάτου, οι ερευνητές μπορούν να χρησιμοποιήσουν μελέτες σειράς στις οποίες παρακολουθούν μια ομάδα ατόμων που έχουν προσβληθεί πρόσφατα, έως ότου ο καθένας είτε ανακάμψει είτε πεθάνει. Η διενέργεια τέτοιων μελετών είναι δύσκολη κατά τη διάρκεια ενός συνεχιζόμενου κρούσματος. Εναλλακτικά, οι απλές μετρήσεις αναλογίας θανάτου μπορούν να προσαρμοστούν ώστε να λαμβάνουν υπόψη την ανάπτυξη της επιδημίας και τον χρόνο έως το θάνατο.
Ένας άλλος περίπλοκος παράγοντας κατά τον υπολογισμό του CFR είναι να προσδιοριστεί ποιος λαμβάνεται ως περίπτωση. Οι ορισμοί του CFR στη βιβλιογραφία επιδημιολογίας καθιστούν σαφές ότι μια περίπτωση είναι κάποιος που να έχει διαγνωστεί με λοίμωξη, είτε με ένα συγκεκριμένο τεστ είτε τουλάχιστον με βάση τα συμπτώματα. Αλλά αυτό είναι ένα πρόβλημα για λοιμώξεις όπως το COVID-19, δεδομένου ότι οι πραγματικές περιπτώσεις είναι ανεπαρκείς λόγω των περιορισμένων τεστ και των ασυμπτωματικών μολύνσεων. Εάν οι ερευνητές θέλουν πραγματικά να εκτιμήσουν την πιθανότητα λοίμωξης από θάνατο, τότε πρέπει να διορθώσουν αυτήν την υποτιμημένη μέθοδο. Η ποσότητα που υπολογίζεται στη συνέχεια ονομάζεται πιο σωστά κίνδυνος θνησιμότητας από μόλυνση (IFR). Για να εκτιμήσουν το βαθμό υποτιμήσεως και να υπολογίσουν το IFR για το COVID-19, οι επιδημιολόγοι είτε εξετάζουν πληθυσμούς με σχεδόν καθολικά τεστ είτε διεξάγουν τυχαίες δοκιμές σε επίπεδο πληθυσμού για να εκτιμήσουν τον επιπολασμό της τρέχουσας ή προηγούμενης μόλυνσης.
Άλλες προκλήσεις, όπως η σωστή αναγνώριση της αιτίας θανάτου, επηρεάζουν επίσης εκτιμήσεις και ερμηνείες των τιμών CFR και IFR για το COVID-19 και άλλων λοιμώξεων. Αλλά το πιο σημαντικό, μετρήσεις όπως το CFR υπολογίζουν μόνο τους θανάτους. Δεν περιλαμβάνουν τις πολλές άλλες ζημιές που υφίστανται οι επιζώντες. Οι μακροχρόνιες επιπλοκές του COVID-19 και η απαιτούμενη φροντίδα για σοβαρές περιπτώσεις, όπως η μηχανική παροχή οξυγόνου, βρίσκονται ακόμη υπό διερεύνηση και απλές μετρήσεις είναι απίθανο να συλλάβουν αυτά τα αποτελέσματα.
Από την περιγραφή στην πρόβλεψη
Μετρήσεις όπως τα R0, r , και το CFR, βοηθούν στην ταξινόμηση και σύγκριση των λοιμώξεων και τη γρήγορη επικοινωνία του κινδύνου. Ωστόσο, η ικανότητά τους να προβλέπουν το πλήρες βάρος μιας επιδημίας είναι περιορισμένη. Για παράδειγμα, το πόσα άτομα σκοτώνει μια λοίμωξη και η χρονική κλίμακα στην οποία συμβαίνει, εξαρτάται όχι μόνο από το CFR, αλλά και από τον αριθμό των ατόμων που μολύνονται, το οποίο εξαρτάται από το πόσο εύκολα μεταδίδεται η λοίμωξη, ποιο ποσοστό του πληθυσμού είναι ευαίσθητο, και την αποτελεσματικότητα των μέτρων ελέγχου. Ο αριθμός των νέων καθημερινών λοιμώξεων εξαρτάται από τον αριθμό των ατόμων που έχουν μολυνθεί επί του παρόντος και πόσο καιρό πριν μολύνθηκαν, γεγονός που καθορίζει πόσα από αυτά έχουν ήδη εισέλθει στη μολυσματική περίοδο τους. Για να συγκεντρώσουμε αυτές τις ιδέες και να κάνουμε ενημερωμένες προβλέψεις, χρειάζονται μαθηματικά μοντέλα.
Τα περισσότερα δυναμικά μοντέλα που χρησιμοποιούνται για την παρακολούθηση της εξάπλωσης της λοίμωξης σε έναν πληθυσμό είναι διαμεριστικά μοντέλα, στα οποία τα άτομα ταξινομούνται σε μία από τις λίγες διακριτές καταστάσεις, όπως ευαίσθητα, μολυσματικά ή ανακτημένα, με βάση την κατάσταση μόλυνσής τους (βλέπε Εικόνα 3). Το μοντέλο παρακολουθεί τις αλλαγές στον αριθμό των ατόμων σε κάθε κατάσταση, συνήθως με διαφορικές εξισώσεις ή διακριτές ή συνεχείς στοχαστικές διαδικασίες. Οι εξισώσεις είναι εγγενώς μη γραμμικές επειδή οι αλληλεπιδράσεις μεταξύ των ευπαθών και των μολυσματικών ατόμων δημιουργούν νέες μολύνσεις.
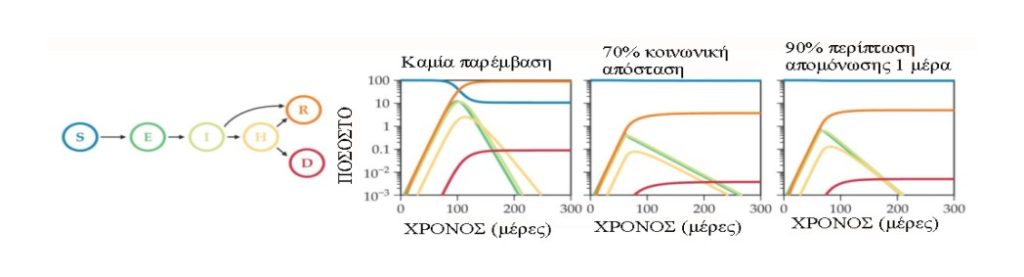
Μερικά απλά πρότυπα μοντέλα επιδημίας θα είναι γνωστά στους φυσικούς από εισαγωγικά μαθήματα δυναμικών συστημάτων και ονομάζονται από τα ακρωνύμια των επί μέρους στοιχείων τους. Για παράδειγμα, το μοντέλο SIS περιγράφει λοιμώξεις, όπως πολλές σεξουαλικά μεταδιδόμενες ασθένειες, που δεν παράγουν μακροχρόνια ανοσία: τα ευπαθή άτομα (S) μπορούν να γίνουν μολυσματικά (Ι) αλλά στη συνέχεια να επιστρέψουν στην ευπαθή κατάσταση όταν αναρρώσουν. Στο μοντέλο SIR, τα ανακτημένα άτομα (R) υποτίθεται ότι είναι μόνιμα ανοσοποιητικά, μια καλή προσέγγιση για πολλές βραχυπρόθεσμες ιογενείς λοιμώξεις όπως η ιλαρά ή ο κίτρινος πυρετός.
Όπως οι φυσικοί, οι ερευνητές λοιμωδών νοσημάτων εξισορροπούν τη δημιουργία απλών, κατανοητών μοντέλων με τη δημιουργία χρήσιμων προβλέψεων. Τα διαμεριστικά μοντέλα είναι πάντοτε υπεραπλουστεύσεις, διότι στην πραγματικότητα, η μόλυνση στο σώμα ενός ατόμου είναι ένα σύνολο καταστάσεων – το μικρόβιο πολλαπλασιάζεται και μεταναστεύει μεταξύ των ιστών, το ανοσοποιητικό σύστημα ααντιδρά και τα συμπτώματα αναπτύσσονται. Και η διαδικασία μετάδοσης ασθενειών μπορεί να είναι πολύ πιο περίπλοκη από τους απλούς όρους του ποσοστού αντίδρασης που χρησιμοποιούνται σε πολλές εξισώσεις. Εξαρτάται από τις προσωπικές επαφές και την εξαιρετικά δομημένη φύση των κοινωνικών δικτύων. (Δες Πλαίσιο 3)
Πλαίσιο 3. Προσομοίωση εξάπλωσης μόλυνσης σε δίκτυα
Οι ανθρώπινες επαφές δεν είναι τυχαίες ή ομοιόμορφα κατανεμημένες. Μπορούν να περιγραφούν από ένα δίκτυο επαφών που καθορίζει ποιες διαδρομές μετάδοσης είναι δυνατές εάν μια λοίμωξη εισαχθεί στον πληθυσμό. Η δομή του δικτύου μπορεί να επηρεάσει σε μεγάλο βαθμό την έκταση της εξάπλωσης των ασθενειών.
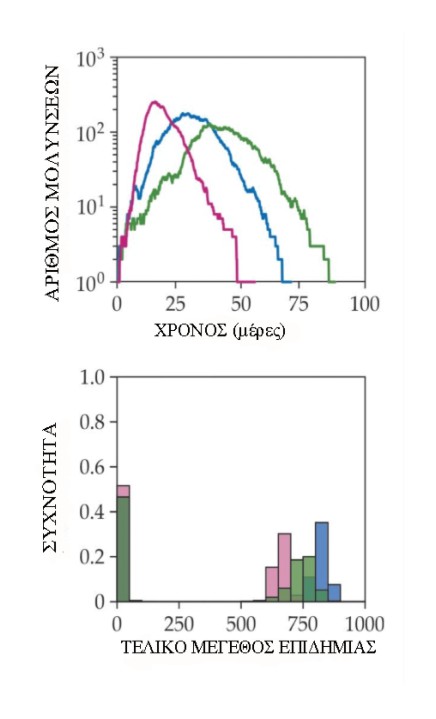
Εδώ, ένα απλό, στοχαστικά προσομοιωμένο μοντέλο ευπαθών μολυσμένων-ανακτημένων (SIR) καταδεικνύει αυτή την ιδέα σε τρία εξιδανικευμένα δίκτυα: ένα ομοιόμορφο τυχαίο δίκτυο, στο οποίο κάθε άτομο συνδέεται με 10 άλλα τυχαία επιλεγμένα άτομα, ένα δίκτυο μικρού κόσμου, με υψηλή συγκέντρωση που χρησιμοποιεί ο αλγόριθμος Watts – Strogatz για σύνδεση κατά προτίμηση ατόμων σε 10 γείτονες και, στη συνέχεια, επανασυνδέει τυχαία το 10% των συνδέσεων και ένα ετερογενές δίκτυο στο οποίο ο αριθμός των γειτόνων για κάθε άτομο προέρχεται από μια κατανομή γάμμα με μέση και τυπική απόκλιση 10. Όλες οι επιδημίες ξεκίνησε με ένα μολυσμένο άτομο.
Η επιδημική ανάπτυξη είναι ταχύτερη στα ετερογενή δίκτυα και ενισχύεται από υπερσυνδεδεμένους υπερμεταδότες. Είναι πιο αργό στο δίκτυο μικρού κόσμου, όπου ο υψηλός βαθμός διασύνδεσης περιορίζει τις ευαίσθητες επαφές που έχει δει ένα μολυσμένο άτομο. Το τελικό μέγεθος της επιδημίας – το ποσοστό των ατόμων που έχουν ανανήψει, όταν η λοίμωξη τελικά εξαφανιστεί – ποικίλλει ανάλογα με τις στοχαστικές επιδράσεις, αλλά είναι γενικά υψηλότερο στο ομοιόμορφο δίκτυο και χαμηλότερο στο ετερογενές δίκτυο.
Το επίπεδο λεπτομέρειας που απαιτείται για να είναι χρήσιμο ένα μοντέλο εξαρτάται από το σκοπό του. Ορισμένοι ερευνητές που μοντελοποιούν το COVID-19 ενδιαφέρονται να κατανοήσουν την πιθανή επιβάρυνση του συστήματος υγειονομικής περίθαλψης, οπότε να επεκτείνουν τα μοντέλα τύπου SIR ώστε να περιλαμβάνουν προχωρημένα στάδια λοίμωξης που απαιτούν νοσηλεία ή εισαγωγή σε μονάδα εντατικής θεραπείας. Παρακολουθούν επίσης το ποσοστό των ατόμων που πεθαίνουν (βλ. Εικόνα 3). Σε μελέτες που κάνουν συστάσεις πολιτικής σχετικά με τις στρατηγικές κοινωνικής απόστασης, οι μοντελιστές προσομοιώνουν λεπτομερή δίκτυα μόλυνσης, που περιγράφουν τις αλληλεπιδράσεις των ατόμων στο σπίτι, το σχολείο και την εργασία και μεταξύ φίλων. Για να κατανοήσουν την αποτελεσματικότητα της απομόνωσης με βάση τα συμπτώματα με ή χωρίς πρόσθετη απομόνωση επαφών, οι επιστήμονες αυξάνουν τα βασικά μοντέλα για να παρακολουθούν τη μολυσματικότητα κατά τη διάρκεια της νόσου.
Οι επιστήμονες συζητούν συνεχώς τα σχετικά πλεονεκτήματα και τις επιφυλάξεις διαφορετικών προσεγγίσεων μοντελοποίησης για το COVID-19. Βελτιώνουν τα μοντέλα καθώς η κατανόησή τους για την ασθένεια αλλάζει και προσπαθούν να προσδιορίσουν τον τρόπο να επικοινωνούν καλύτερα με κοινό με την εγγενή αβεβαιότητα στις προβλέψεις των μοντέλων.
Η μαθηματική ανάλυση και μοντελοποίηση είναι βασικά εργαλεία στη μελέτη των μολυσματικών ασθενειών και υπήρξαν κρίσιμα στην απάντησή μας στην πανδημία COVID-19. Εκτίμηση ακόμη και φαινομενικά απλών μετρήσεων – R0 , CFR, και περίοδος επώασης και μόλυνσης, μεταξύ άλλων – απαιτεί αυστηρή προσοχή στις αποχρώσεις των δεδομένων και προσεκτική διαμόρφωση μαθηματικών σχέσεων. Κατά το σχεδιασμό σύνθετων δυναμικών μοντέλων επιδημίας, οι μοντελιστές κάνουν ανταλλαγές μεταξύ της διατήρησης των πραγμάτων σε αρκετά απλό επίπεδο, για να διευκολύνουν την κατανόηση, και σε αρκετά ρεαλιστικό για να κάνουν ακριβείς προβλέψεις. Η σωστή επιλογή των αριθμών είναι πάντα προτεραιότητα για τους επιστήμονες. Κατά τη διάρκεια μιας κρίσης στη δημόσια υγεία, οι διακυβεύσεις είναι υψηλότερες από ποτέ.