Δυναμική στο Επίπεδο: Δράση-Αντίδραση, Σύνθεση-Ανάλυση Δυνάμεων

Το Διάγραμμα Ελεύθερου Σώματος (ΔΕΣ)

Πριν ο μαθητής προχωρήσει στη λύση ασκήσεων και στην απάντηση ερωτήσεων, είναι χρήσιμο να κατανοήσει τι είναι, πώς κατασκευάζεται και πώς βοηθάει το Διάγραμμα Ελεύθερου Σώματος στη διαδικασία της λύσης.

Το ΔΕΣ είναι ένα διάγραμμα που δείχνει τα σχετικά μέτρα και τις κατευθύνσεις όλων των δυνάμεων που ασκούνται πάνω σε ένα σώμα, σε μια δεδομένη κατάσταση.

Οι δυνάμεις απεικονίζονται με διανύσματα (βέλη). Τα μήκη των διανυσμάτων πρέπει να αντιστοιχούν στα μέτρα των δυνάμεων και οι κατευθύνσεις τους δείχνουν τις κατευθύνσεις των δυνάμεων.

Τα σώματα συνήθως τα σχεδιάζουμε ως μικρά παραλληλόγραμμα, με τις  δυνάμεις να ασκούνται στο κέντρο τους ή σημεία, με τις δυνάμεις να ασκούνται στο σημείο που εκφράζει το σώμα. Ας μη ξεχνάμε ότι οι διαστάσεις των σωμάτων, σ’ αυτή τη φάση, δε μας ενδιαφέρουν και όλα τα σώματα τα θεωρούμε ως υλικά σημεία.

Όταν κατασκευάζουμε για ένα σώμα το ΔΕΣ, σχεδιάζουμε μόνο το σώμα αυτό με τις δυνάμεις που ασκούνται επάνω του και κανένα άλλο, έστω κι αν το σώμα βρίσκεται σε απαφή με άλλα. Π.χ. ας υποθέσουμε ότι έχουμε πάνω σε μία οριζόντια επιφάνεια ακίνητο ένα αντικείμενο Σ [Εικ. 1(α)]. Στην Εικ. 1 (β) και Εικ. 1 (γ) είναι τα διαγράμματα ελεύθερου σώματος του αντικειμένου Σ και της επιφάνειας αντίστοιχα.

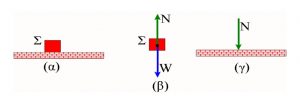
Εικ. 1: (α) Το σώμα Σ ακίνητο πάνω σε μία οριζόντια επιφάνεια. (β) ΔΕΣ του Σ. Το Σ έχει σχεδιαστεί ως μικρό παραλληλόγραμμο και επάνω του ασκούνται το βάρος του W και η κάθετη δύναμη Ν της επιφάνειας. (γ) ΔΕΣ της επιφάνειας. Στην επιφάνεια ασκείται η δύναμη Ν, με βάση το νόμο Δράσης-Αντίδρασης του Νεύτωνα. Οι δύο δυνάμεις W και N σχεδιάστηκαν με ίσα μήκη.

Δες και το άρθρο του Albert Lee “Πώς σχεδιάζουμε ένα σωστό Διάγραμμα Ελευθέρου Σώματος”

Στις ασκήσεις που ακολουθούν όλα τα σχοινιά και νήματα θεωρούνται αβαρή. Αβαρείς και χωρίς διαστάσεις θεωρούνται και οι τροχαλίες. Επίσης, όπου δεν αναφέρεται ρητά ότι οι επιφάνειες είναι λείες, να λαμβάνονται υπόψη οι τριβές.

1. Το μπαλάκι του τένις κτυπάει στη ρακέτα και επιστρέφει με αντίθετη κατεύθυνση.
   1. Σχεδίασε το διάγραμμα ελεύθερου σώματος για το μπαλάκι και τη ρακέτα.
   2. Το μπαλάκι, που έχει μάζα 58,5gr, πέφτει πάνω στη ρακέτα με ταχύτητα 40m/s και επιστρέφει με -60m/s. Να συγκρίνεις τις δυνάμεις που αλληλεπιδρούν το μπαλάκι και η ρακέτα, στον μικρό χρόνο του 1ms που είναι σε επαφή μεταξύ τους. Με πόση δύναμη κτυπάει τη ρακέτα το μπαλάκι;
   

   Άσκηση 1

2. Κρατάμε τη σφαίρα Σ ακίνητη μέσω ενός κατακόρυφου νήματος. Σχεδίασε τα διαγράμματα ελεύθερου σώματος για το Σ, το νήμα και το χέρι.
   

   Άσκηση 2

3. Ο αθλητής τραβάει τον ελέφαντα. Σχεδίασε τη δύναμη που ασκείται στο χέρι του αθλητή, στην προβοσκίδα του ελέφαντα και σύγκρινε τις δύο δυνάμεις.
   

   Ερώτηση 3

4. Στη μέση της επιφάνειας του τραπεζιού είναι τοποθετημένο ένα βιβλίο. Να σχεδιάσεις τα διαγράμματα ελεύθερου σώματος του βιβλίου, του τραπεζιού και της οριζόντιας επιφάνειας του δαπέδου.
   

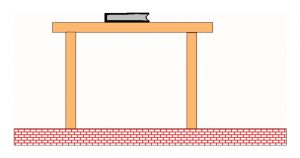
   Άσκηση 4

5. Το σώμα Σ σέρνεται πάνω σε οριζόντια επιφάνεια με τη βοήθεια ενός σχοινιού. Το σχοινί το τραβάει προς τα δεξιά ένας άνθρωπος ασκώντας στο άκρο του Α δύναμη F.
   1. Σχεδίασε τα διαγράμματα ελεύθερου σώματος για το Σ, την οριζόντια επιφάνεια, το σχοινί και το χέρι του ανθρώπου.
   2. Στο διάγραμμα του σώματος Σ ανάλυσε τη δύναμη F σε μία οριζόντια και μία κατακόρυφη συνιστώσα. (Επειδή οι διαστάσεις των σωμάτων δε μας ενδιαφέρουν προς το παρόν, μπορείς να σχεδιάσεις όλες τις δυνάμεις που ασκούνται στο Σ να έχουν ως σημείο εφαρμογής το κέντρο μάζας του σώματος).
   

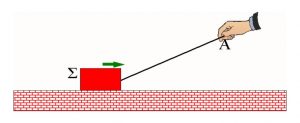
   Άσκηση 5

6. Το σώμα Σ₁ κινείται επιταχυνόμενο εξ αιτίας της δύναμης F και τραβάει μαζί του, με τη βοήθεια νήματος, το σώμα Σ₂. Σχεδίασε το διάγραμμα ελεύθερου σώματος για τα δύο σώματα σε δύο περιπτώσεις:
   1. Όταν η κίνηση γίνεται σε λεία επιφάνεια.
   2. Όταν η κίνηση γίνεται σε τραχεία επιφάνεια και υπάρχουν τριβές.
   

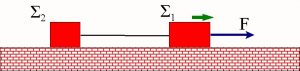
   Άσκηση 6

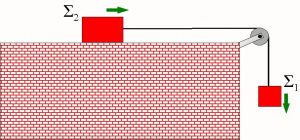
7. Αφήνουμε το σώμα Σ₁ ελεύθερο να κινηθεί κατακόρυφα και αυτό παρασέρνει σε κίνηση το σώμα Σ₂ μέσω του νήματος που είναι δεμένο με το Σ₁, Να σχεδιάσεις τα διαγράμματα ελεύθερου σώματος για τα Σ₁ και Σ₂ σε δύο περιπτώσεις:
   1. Όταν το Σ₂ κινείται σε λεία επιφάνεια.
   2. Όταν η κίνηση του το Σ₂ κίνεται σε τραχεία επιφάνεια και υπάρχουν τριβές.
   

   Άσκηση 7

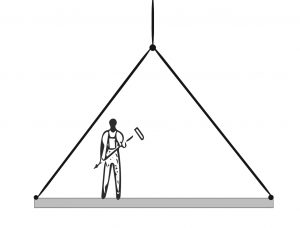
8. Ο εργάτης βρίσκεται πάνω στην οριζόντια δοκό, η οποία είναι κρεμασμενη από δύο σχοινιά έτσι ώστε η δοκός και τα σχοινιά να σχηματίζουν τρίγωνο. Να σχεδιάσεις τα διαγράμματα ελεύθερου σώματος του εργάτη, της δοκού και των δύο σχοινιών.
   

   Άσκηση 8

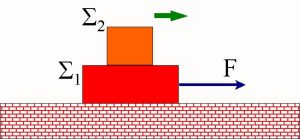
9. Το σώμα Σ₂ είναι απλώς τοποθετημένο πάνω στο Σ₁. Το Σ₁ το τραβάμε με δύναμη F. Αν υποθέσουμε ότι η κίνηση του Σ₁ γίνεται πάνω σε λεία οριζόντια επιφάνεια και ότι επίσης λείες είναι και οι επιφάνειες των δύο σωμάτων, να σχεδιάσεις τα διαγράμματα ελεύθερου σώματος για τα δύο σώματα. Τι θα συμβεί στο Σ₂ μόλις ασκήσουμε τη δύναμη F στο Σ₁; Επανάλαβε όλα τα παραπάνω και απάντησε στην ίδια ερώτηση, στην περίπτωση που υπάρχει τριβή μεταξύ του Σ₁ και της οριζόντιας επιφάνειας και μεταξύ των Σ₁ και Σ₂.
   

   Άσκηση 9

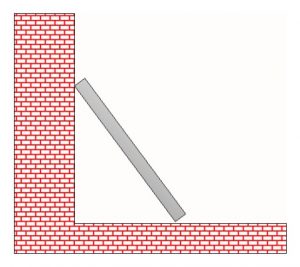
10. Πάνω σε έναν τοίχο είναι ακουμπισμένη ένα βαριά σανίδα. Αν η σανίδα ακουμπάει σε λείο τοίχο και σε τραχύ δάπεδο, να σχεδιάσεις το διάγραμμα ελεύθερου σώματος της σανίδας.
    

    Άσκηση 10

11. Τα σώματα Σ₁ και Σ₂ είναι σε επαφή. Σπρώχνουμε το Σ₁ με τη δύναμη F και θέτουμε το σύστημα των δύο σωμάτων σε κίνηση. Να σχεδιάσεις τα διαγράμματα ελεύθερου σώματος για τα Σ₁ και Σ₂ σε δύο περιπτώσεις:
    1. Όταν τα σώματα κινούνται σε λεία επιφάνεια.
    2. Όταν η οριζόντια επιφάνεια που κινούνται τα σώματα είναι τραχεία.
    

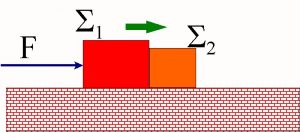
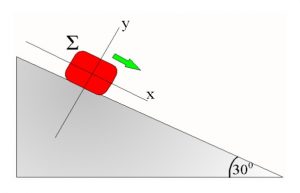
    Άσκηση 11

12. Το σώμα Σ, μάζας 20kg, γλιστράει προς τα κάτω χωρίς τριβές, στην επιφάνεια κεκλιμένου επιπέδου γωνίας 30⁰.
    1. Να σχεδιάσεις το διάγραμμα ελεύθερου σώματος του Σ.
    2. Να αναλύσεις τη δύναμη του βάρους του Σ σε δύο συνιστώσες, F_x και F_y, κατά τους άξονες x και y αντίστοιχα και να τις υπολογίσεις.

    Δίνονται: g=10m/s², ημ30⁰=0,5 και συν30⁰=0,87.

    

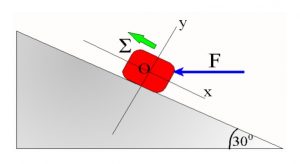
    Άσκηση 12

13. Στο σώμα Σ μάζας 4kg ασκείται η οριζόντια δύναμη F=100N, η οποία το κινεί προς τα πάνω στο κεκλιμένο επίπεδο γωνίας 30⁰.Στο σώμα ασκείται τριβή 10Ν.
    1. Σχεδίασε το διάγραμμα ελεύθερου σώματος του Σ.
    2. Να αναλύσεις όλες τις δυνάμεις κατά τους άξονες x και y και να υπολογίσεις τις συνιστώσες των δυνάμεων.
    3. Να βρεις τη συνισταμένη των δυνάμεων ΣF_x κατά τον άξονα των x και ΣF_y κατά τον άξονα y.
    

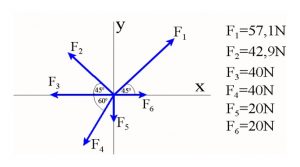
    Άσκηση 13

14. Έξι δυνάμεις ασκούνται στο ίδιο σημείο. Τα μέτρα και οι κατευθύνσεις τους φαίνονται στην εικόνα.
    1. Να αναλύσεις όλες τις δυνάμεις σε δύο συνιστώσες κατά τους έξονες x και y και να υπολογίσεις τα μέτρα των συνιστωσών.
    2. Να υπολογίσεις τη συνισταμένη ΣF_x κατά τον άξονα x και ΣF_y κατά τον άξονα y.
    3. Υπολόγισε κατά μέτρο διεύθυνση και φορά τη συνισταμένη ΣF των ΣF_x και ΣF_y.

    Δίνονται: ημ45⁰=0,7, συν45⁰=0,7, ημ60⁰=0,9, συν60⁰=0,5.

    

    Άσκηση 14

15. Στο σώμα μάζας 25kg ασκούνται οι δυνάμεις F₁=40Ν και F₂=30Ν, που σχηματίζουν γωνίες 30⁰ και 60⁰ με τη οριζόντια διεύθυνση αντίστοιχα. Προς ποια κατεύθυνση σε σχέση με τη οριζόντια και με πόση επιτάχυνση θα κινηθεί το σώμα, αν επάνω του ασκούνται μόνο οι δύο αυτές δυνάμεις και ξεκινάει από την ηρεμία;
    

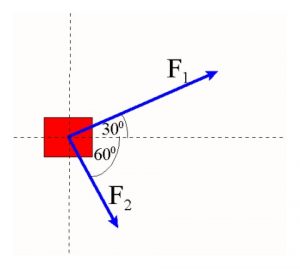
    Άσκηση 15

16. Βρες τη συνισταμένη των δύο ίσων κατά μέτρο δυνάμεων που σχηματίζουν μεταξύ τους γωνία 120⁰.
    

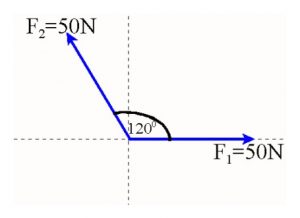
    Άσκηση 16

17. Βρες τη συνισταμένη κατά διεύθυνση, φορά και μέτρο, δύο δυνάμεων F₁=80Ν και F₂ =50Ν που σχηματίζουν μεταξύ τους 60⁰ και ασκούνται στο ίδιο σημείο. Δίνονται:  ημ30⁰=0,5, συν30⁰=0,9.
    

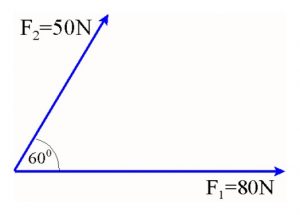
    Άσκηση 17

18. Να αναλύσεις μία δύναμη 100Ν σε δύο συνιστώσες που να σχηματίζουν με αυτήν γωνία 45⁰ η κάθε μία. Σημείωση: Όταν λέμε “να αναλύσεις” εννοούμε να κάνεις διάγραμμα των διανυσμάτων και να υπολογίσεις τα μέτρα τους.
19. Να αναλύσεις μία δύναμη F=100Ν σε δύο συνιστώσες ώστε η μία να έχει μέτρο 50Ν και η άλλη να σχηματίζει γωνία 30⁰ με την F. Δίνεται: συν60⁰=0,5.
20. Να αναλύσεις μία δύναμη F=100Ν σε δύο συνιστώσες F₁ και F₂ ώστε η F₁ να είναι κάθετη στην F και η F₂ να σχηματίζει γωνία 30⁰ με την F. Δίνονται:  ημ30⁰=0,5, συν30⁰=0,9.
21. Να αναλύσεις μία δύναμη F=100Ν σε δύο συνιστώσες ώστε η μία να σχηματίζει με αυτήν γωνία 60⁰ και να είναι ίση στο μέτρο με τη την F.

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

Κράτα το

Κράτα το

Κράτα το