Η αναζήτηση της φύσης του ηλεκτρονίου και της φύσης του φωτός αποτέλεσαν δύο από τα μεγαλύτερα προβλήματα της Φυσικής και λαμπρό πεδίο ερευνών όλων των μεγάλων επιστημόνων. Ο καθηγητής-ερευνητής Don Licoln του Fermilab στο Σικάγο, ΗΠΑ, μας έχει δώσει πολλά άρθρα με τα οποία εκλαϊκεύει σύνθετες έννοιες της φυσικής, έτσι ώστε να δίνει την ευκαιρία σε όλους όσους διαθέτουν ένα σχετικά ανεκτό επίπεδο γνώσεων, να μπορούν να αντιλαμβάνονται τους βαθύτερους μηχανισμούς που διέπουν τα φυσικά φαινόμενα.
Στο παρακάτω άρθρο αναλύει σε σημαντικό βάθος τη φύση του ηλεκτρονίου, για το οποίο εκείνο που όλοι γνωρίζουμε είναι ότι πρόκειται για ένα μικρότατο σωματίδιο, συστατικό του κάθε ατόμου, έχει αρνητικό φορτίο και περιστρέφεται γύρω από τον πυρήνα. Πόσο κοντά στην πραγματικότητα είμαστε; Μήπως μπροστά μας έχουμε ένα πολύ πιο σύνθετο αντικείμενο, για το οποίο πολλά γνωρίζουμε, αλλά ακόμη πιο πολλά έχουμε να μάθουμε;
- Του Don Licoln, καθηγητή-ερευνητή στο Fermilab, Chicago
- Από το The Physics Teacher Magazine
Ο Winston Churchill είπε κάποτε ότι η Ρωσία ήταν ένα αίνιγμα τυλιγμένο στο μυστήριο μέσα σε ένα αίνιγμα. Αν το “Εγγλέζικο Μπουλντόγκ” ήταν φυσικός, θα μπορούσε να μιλήσει για κάτι άλλο, εκτός από τους Σλάβους συντρόφους μας. Θα μπορούσε να μιλήσει για το ηλεκτρόνιο.
Μπορεί να φαίνεται περίεργο να σκεφτούμε το ηλεκτρόνιο ως ένα μυστηριώδες σωματίδιο. Εξ άλλου, εκπαιδευτικοί που διδάσκουν εισαγωγική φυσική, διδάσκουν παντού τους μαθητές για το φορτίο και το ρεύμα και κάνουν εργαστήρια για τον υπολογισμό του λόγου φορτίου προς μάζα του σωματιδίου. Αν είναι αρκετά εύκολο να καταλάβουμε ότι μπορούμε να παρουσιάσουμε τις τεχνικές λεπτομέρειες του σωματιδίου στους πρωτοετείς φοιτητές της φυσικής, τότε πόσο μυστηριώδες μπορεί να είναι;
Βέβαια, πιθανώς τώρα να γύρισαν οι σκέψεις σας στην κβαντική των ηλεκτρονίων και την εξίσωση του Schrödinger και στο αν οι γάτες είναι ζωντανές ή νεκρές, και ίσως αρχίσετε να θυμόσαστε ότι το ηλεκτρόνιο δεν μας έχει πει όλες τις ιστορίες του. Και η ιστορία της κβαντικής μηχανικής είναι πλέον παλιά, σχεδόν έναν αιώνα. Η επιστήμη έχει προχωρήσει και οι ερευνητές έχουν εγκαταλείψει τις απλούστερες κβαντικές παραστάσεις του ηλεκτρονίου για τις πιο προηγμένες της σχετικιστικής κβαντομηχανικής και της θεωρίας των κβαντικών πεδίων. Όπως η Σαλώμη, στην όπερα του Ρίχαρντ Στράους, το ηλεκτρόνιο φαίνεται να κάνει το χορό των επτά πέπλων και ο χορός δεν έχει ακόμη τελειώσει. Το ηλεκτρόνιο έχει ακόμα μερικά μυστικά να αποκαλύψει.
Αυτό το άρθρο θα καλύψει κυρίως τις πιο σύγχρονες αναπαραστάσεις του ηλεκτρονίου. Η ιστορία θα ξεκινήσει με μια σύντομη υπενθύμιση των ηλεκτρονίων της κλασικής φυσικής και των αρχών της κβαντικής θεωριάς, αλλά αυτά θα χρησιμοποιηθούν μόνο ως εφααλτήρια για να βυθιστούμε στην ιστορία των σύγχρονων ηλεκτρονίων. Και, όπως θα δούμε, αυτή η ιστορία πηγαίνει πολύ βαθιά.
Το αρχικό ηλεκτρόνιο

Εικ. 1. Μία συσκευή σαν το σωλήνα του Crookes, που εικονίζεται εδώ, επέτρεψε στους φυσικούς του 19ου αιώνα να μελετήσουν τις καθοδικές ακτίνες, ως μία πρώτη προσπάθεια να αντιληφθούν αυτό που σήμερα αποκαλούμε ηλεκτρόνιο.
Πριν μάθουμε για τα ηλεκτρόνια, γνωρίζαμε τις καθοδικές ακτίνες (Εικ. 1). Οι ακτίνες αυτές εκπέμπονται όταν σε ένα σωλήνα κενού τοποθετήσουμε δύο μεταλλικές πλάκες. Όταν μεταξύ των δύο μεταλλικών πλακών εφαρμοστεί υψηλή ηλεκτρική τάση, φαίνεται ότι κάποιο είδος ακτίνων βγαίνει από την κάθοδο (αρνητικά φορτισμένη πλάκα) και κατευθύνεται προς τη θετική πλάκα. (Ενώ οι περισσότεροι αναγνώστες θα γνωρίζουν ότι ένα νήμα χρησιμοποιείται συχνά για να δημιουργηθούν καθοδικές ακτίνες, η θερμιονική εκπομπή είναι απλά πιο αποτελεσματική και όχι απαραίτητη.) Ορισμένες από αυτές τις ακτίνες χτυπούν το γυάλινο περίβλημα, με αποτέλεσμα αυτό να λάμπει αποκαλύπτοντας έτσι την παρουσία τους. Σε μεταγενέστερα πειράματα προστέθηκε φωσφορίζον υλικό στο γυαλί για να ενισχυθεί η λάμψη.

Εικ. 2. Ο Φυσικός J.J. Thomson ανακάλυψε το ηλεκτρόνιο το 1897, ανοίγοντας το δρόμο στη σημερινή κοινωνία της τεχνολογίας.
Από την ανακάλυψή τους το 1869 και στο μεγαλύτερο μέρος των επόμενων τριών δεκαετιών, οι επιστήμονες μελέτησαν τη φύση των καθοδικών ακτίνων και διαπίστωσαν ότι είχαν αρνητικό ηλεκτρικό φορτίο. Ήταν το 1897 όταν ο Βρετανός φυσικός J.J. Thomson (Εικ. 2) απόδειξε ότι οι καθοδικές ακτίνες στην πραγματικότητα αποτελούνται από φορτισμένα σωματίδια που ονόμασε σωμάτια. Διατύπωσε επίσης την άποψη ότι τα σωμάτια αυτά ήταν τα μόνα συστατικά των ατόμων με μάζα, το υπόλοιπο μέρος του ατόμου το φανταζόταν ως ένα άμαζο, θετικά φορτισμένο, πεδίο.
Τα πειράματα του Thomson έδειξαν ότι ο λόγος φορτίου προς μάζα ήταν πολύ μεγάλος, γεγονός που υποδηλώνει ότι τα σωμάτια είτε είχαν μάζα παρόμοια με εκείνη ενός ατόμου υδρογόνου και πολύ μεγάλο φορτίο, ή είχαν ένα φορτίο συγκρίσιμο με ένα ιονισμένο άτομο υδρογόνου και πολύ μικρή μάζα. Ενώ οι μετρήσεις της Thomson ήταν ασαφείς σε αυτό το αίνιγμα, προηγούμενες μετρήσεις από τον Γερμανό φυσικό Phillipp Lenard σχετικά με το πώς οι καθοδικές ακτίνες διεισδύουν στα αέρια, πρότειναν ως πιο πιθανή τη λύση της χαμηλής μάζας. Φυσικά, γνωρίζουμε πλέον ότι το ηλεκτρόνιο και το πρωτόνιο έχουν ίσα ηλεκτρικό φορτίο και πολύ διαφορετικές μάζες. Η μάζα του πρωτονίου είναι περίπου 1836 φορές μεγαλύτερη από τη μάζα του ηλεκτρονίου.
Ενώ ο Thomson ανακάλυψε το ηλεκτρόνιο, το όνομα επινοήθηκε από τον G. Johnstone Stoney το 1891 για να περιγράψει τη μονάδα φορτίου που παρατηρείται σε πειράματα που δημιουργούν ηλεκτρικά ρεύματα στην περίπτωση χημικών ουσιών. Το μοντέλο του ατόμου του Thomson, που αποτελείται από αρνητικά φορτισμένα και μαζικά ηλεκτρόνια ενσωματωμένα μέσα σε ένα άμαζο, θετικά φορτισμένο χώρο, ονομάστηκε το μοντέλο “πουτίγκα δαμάσκηνο” (ή του σταδιδόψωμου). Αλλά αυτό δεν κράτησε πολύ.
Ήταν ο μαθητής του Thomson, ο φυσικός Ernest Rutherford, που γεννήθηκε στη Νέα Ζηλανδία, ο οποίος το 1911 απέρριψε το ατομικό μοντέλο του Thomson και το αντικατέστησε με την ιδέα του ενός πυρηνικού ατόμου, που αποτελείται από ένα πυκνό θετικό φορτίο στο κέντρο του ατόμου, με τα ηλεκτρόνια σε τροχιά σε σχετικά μεγάλες αποστάσεις. Εννοιολογικά μπορεί κανείς να οραματίζεται αυτό το μοντέλο ως ανάλογο με ένα ηλιακό σύστημα, με ένα θετικά φορτισμένο πυρηνικό ήλιο και αρνητικά φορτισμένους πλανήτες ηλεκτρονίων.
Ωστόσο, το μοντέλο των ηλεκτρονίων που κινούνται σε τροχιές γύρω από έναν πυρήνα ήταν σαφώς ένα εσφαλμένο μοντέλο. Το ξέρουμε αυτό, επειδή η συμβατική ηλεκτρομαγνητική θεωρία προέβλεψε κατά τρόπο αδιαμφισβήτητο, ότι η σταθερή ακτινική επιτάχυνση του φορτισμένου ηλεκτρονίου θα έχει ως αποτέλεσμα την εκπομπή ηλεκτρομαγνητικής ακτινοβολίας, οπότε το ηλεκτρόνιο θα χάσει ενέργεια και με σπειροειδή τροχιά θα πέσει στο πυρηνικό κέντρο σε περίπου 16 picoseconds(16·10-12s). Αυτό είναι προφανώς ένα μοιραίο ελάττωμα, καθώς σημαίνει ότι τα άτομα είναι εγγενώς ασταθή. Το πρώτο βήμα για την αντιμετώπιση αυτής της δυσκολίας έγινε το 1913, όταν ο Δανός φυσικός Niels Bohr συμπέρανε ότι τα ηλεκτρόνια θα μπορούσαν να υπάρχουν στα άτομα μόνο σε σταθερές τροχιές με συγκεκριμένες ακτίνες. Αυτό το χρήσιμο μοντέλο βελτιώθηκε μετά, όταν ο Γάλλος φυσικός Louis de Broglie στη διδακτορική του διατριβή το 1924 διατύπωσε την άποψη ότι τα ηλεκτρόνια στην πραγματικότητα είναι κύματα. Οι σταθερές τροχιές που ισχυρίστηκε ο Bohr, θα μπορούσαν να γίνουν καλύτερα κατανοητές αν τα διάφορα ατομικά τροχιακά ήταν τελικά στάσιμα κύματα ηλεκτρονίων.
Όταν άκουσε για τις ιδέες του de Broglie, ο Ολλανδός φυσικός Peter Debye έκανε ένα αυθόρμητο σχόλιο, ότι αν τα ηλεκτρόνια ήταν κύματα, τότε θα έπρεπε να περιγράφονται από μια κυματική εξίσωση. Αυτό το σχόλιο ώθησε τον Αυστριακό φυσικό Erwin Schrödinger να δημιουργήσετε αυτό που τώρα καλείται εξίσωση Schrödinger, η οποία περιγράφει τη συμπεριφορά της ύλης κάτω από την επίδραση του δυναμικού. Οι φυσικές καταστάσεις επιλύονται με την εφαρμογή αυτής της εξίσωσης και των συνοριακών συνθήκών και των συνθηκών συνέχειας. Ίσως η πιο οικεία στους φυσικούς λύση είναι η εφαρμογή της εξίσωσης Schrödinger στο άτομο του υδρογόνου. Αυτό έχει ως αποτέλεσμα συναρτήσεις κυμάτων, που αντιστοιχούν στα s, ρ, d, και f τροχιακά που συνήθως διδάσκονται σε εισαγωγικά μαθήματα χημείας.
Η φυσική σημασία της κυματοσυνάρτησης έχει συζητηθεί πολύ. Η πιο κοινή ερμηνεία ονομάζεται Ερμηνεία της Κοπεγχάγης, η οποία επινοήθηκε, κατά το χρονικό διάστημα 1925-1927, από τον Niels Bohr και το Γερμανό φυσικό Werner Heisenberg. Το όνομα προέρχεται από τoν τόπο του ινστιτούτου του Bohr, το οποίο επισκεπτόταν ο Heisenberg. Στην ουσία, η κυματοσυνάρτηση, όταν πολλαπλασιάζεται με τον μιγαδικό συζυγή της, μας δίνει την πιθανότητα του ηλεκτρονίου να έχει μία συγκεκριμένη ενέργεια ή θέση. Πριν από την ανίχνευση, το ηλεκτρόνιο θεωρείται ότι έχει αναρίθμητες πιθανές ενέργειες και θέσεις και μόνο μέσω της ανίχνευσης η κυματοσυνάρτηση “καταρρέει” και προσδιορίζεται για το ηλεκτρόνιο μια ειδική τιμή για τη μεταβλητή που ερευνούμε.
Αναπτύσσοντας μια σύγχρονη θεωρία των ηλεκτρονίων
Η εξίσωση του Schrödinger ήταν ένα τεράστιο βήμα προς τα εμπρός στην κατανόηση της φύσης του ηλεκτρονίου, αλλά είχε τα όριά της. Το πρώτο θέμα ήταν ότι αγνόησε τον τρόπο με τον οποίο ο εσωτερικός μαγνητισμός του ηλεκτρονίου αλληλεπιδράει με ένα κλασικό ηλεκτρομαγνητικό πεδίο. Ο περιορισμός αυτός διατυπώθηκε για πρώτη φορά το 1927 από τον Αυστριακό φυσικό Wolfgang Pauli, όταν αυτός επέκτηνε τη συνάρτηση του Schrödinger για να συμπεριληφθεί αυτή η περίπτωση. Ωστόσο, ακόμη και με αυτή τη σημαντική επέκταση, τόσο οι εξισώσεις Schrödinger όσο και του Pauli ήταν σαφώς μη-σχετικιστικές. Δεδομένου ότι το ηλεκτρόνιο είναι ένα από τα λιγότερο μαζικά υποατομικά σωματίδια και σίγουρα το λιγότερο μαζικό στο άτομο, φάνηκε σαφώς ότι μια σχετικιστική επεξεργασία ήταν κρίσιμη.
Έτσι, αυτά ήταν τα προβλήματα που έπρεπε να επιλυθούν και μέσω αυτής της προσπάθειας άρχισε να αναπτύσσεται η σύγχρονη αντίληψη μας για το ηλεκτρόνιο. Το 1928, ο Βρετανός φυσικός Paul Dirac έγραψε αυτό που σήμερα ονομάζουμε Εξίσωση Dirac. Πρόκειται για μία πλήρως σχετικιστική κυματική εξίσωση. Ήταν μια εκπληκτική επιτυχία. Εκτός από τον αρκετά κοσμικό γάμο της κβαντομηχανικής και της σχετικότητας, ίσως η πιο διάσημη (και αναπάντεχη) συνέπεια της εξίσωσης, ήταν ότι πρόβλεψε την ύπαρξη της αντιύλης, που επαληθεύτηκε πειραματικά λίγα χρόνια αργότερα. Ωστόσο, οι φυσικές συνέπειες της εξίσωσης ήταν ακόμα πιο βαθιές και πιο ουσιώδεις από αυτό. Για παράδειγμα, οι κυματικές συναρτήσεις της θεωρίας του Dirac είναι στην πράξη διανυσματικές, που αποτελούνται από τέσσερις μιγαδικούς αριθμούς. Αυτές οι τέσσερις συνιστώσες θεωρούνται τώρα το ηλεκτρόνιο με +1/2 σπιν, το ηλεκτρόνιο με -1/2 σπιν, το ποζιτρόνιο με σπιν +1/2(η αντιύλη του ηλεκτρονίου), και το ποζιτρόνιο με -1/2 σπιν. Ουσιαστικά, έχει γίνει πλέον κατανοητό, ότι η ύπαρξη του σπιν είναι αναγκαία συνέπεια του γάμου της κβαντικής μηχανικής και της ειδικής σχετικότητας.
Η θεωρία του Dirac όμως δεν είναι χωρίς τις δυσκολίες της. Επειδή η θεωρία είναι μαθηματικά πολύπλοκη, είναι επιλύσιμη μόνο με τη θεωρία των διαταραχών. Ενώ η θεωρία δίνει φυσικά λογικά αποτελέσματα, όταν γίνεται υπολογισμός με τη βασική σειρά της επέκτασης των διαταραχών, δίνει εντελώς παράλογα αποτελέσματα, όταν ο υπολογισμός γίνεται με την επόμενη σειρά της επέκτασης. Στην πραγματικότητα, κάποιες φυσικές ποσότητες προβλέπονται να απειρίζονται. Προφανώς, αυτό δείχνει ότι η θεωρία πάσχει από μια θεμελιώδη ασθένεια, αλλά δεδομένου ότι οι υπολογισμοί κάνουν ουσιαστικές και λογικά ακριβείς προβλέψεις για πολλές μετρήσεις, όπως η μετατόπιση Lamb που περιγράφεται παρακάτω, είναι επίσης σαφές ότι υπάρχει αξία στην εξίσωση του Dirac.
Λίγο μετά τον Δεύτερο Παγκόσμιο Πόλεμο, οι Αμερικανοί φυσικοί Willis Lamb και ο διδακτορικός φοιτητής του Robert Retherford χρησιμοποίησαν μικροκύματα για να βρουν ότι υπήρχε μια μικρή διαφορά ενέργειας μεταξύ των 2P1/2 και 2S1/2 ενεργειακών ηλεκτρονιακών επιπέδων στο υδρογόνο (δηλαδή, του n = 2, l = 1 έναντι του n = 1, l = 0 επιπέδου). Αυτά τα δύο ατομικά τροχιακά επίπεδα προβλέπεται να έχουν την ίδια ενέργεια στη θεωρία του Dirac, επειδή, ενώ η εξίσωση Dirac χειρίζεται τη σύζευξη μεταξύ της τροχιακής στροφορμής του ηλεκτρονίου και της ιδιοπεριστροφής του, το κάνει με έναν τρόπο που είναι ευαίσθητη μόνο για τη συνολική στροφορμή, J, η οποία είναι ίση με 1/2 και στις δύο αυτές καταστάσεις, αλλά όχι για τις μεμονωμένες συνιστώσες της στροφορμής, L, ή το σπιν, σZ, ξεχωριστά (J = L + σZ). Αλλά οι Lamp και Retherford έδειξαν πειραματικά ότι υπήρχε ενεργειακή διαφορά μεταξύ αυτών των δύο επιπέδων που αντιστοιχούν σε διαχωρισμό συχνότητας περίπου 1000 MHz, πυροδοτώντας μια κρίση στην κβαντισμένη ηλεκτρομαγνητική θεωρία, η οποία δεν προβλέπει κανέναν τέτοιο διαχωρισμό συχνοτήτων.
Ο Lamp παρουσίασε την ανάλυσή τους σε συνέδριο τον Ιούνιο του 1947 και το αποτέλεσμα ήταν να οδηγήσει σε γενική σύγχυση τους παρευρισκόμενους. Ο Γερμανός φυσικός Hans Bethe (Εικ. 3) ήταν αυτός ο οποίος εξήγησε με επιτυχία τη μετατόπιση Lamb και έθεσε σε κίνηση το τρένο της σκέψης, που κατέληξε στη σύγχρονη θεωρία της κβαντικής ηλεκτροδυναμικής ή QED. Η εξήγηση Bethe μπορεί να γίνει κατανοητή με μη μαθηματικούς όρους με τον ακόλουθο τρόπο. Ουσιαστικά αυτό που έκανε ήταν να δείξει ότι τα ηλεκτρικά και μαγνητικά πεδία που συνδέονται με το κενό διαταράσσουν το κυρίαρχο ηλεκτρομαγνητικό πεδίο που έχει παραχθεί από τον πυρήνα. Επειδή τα, σε σχήμα αλτήρα, P τροχιακά εξαφανίζονται στο κέντρο του πυρήνα, ενώ τα σφαιρικά τροχιακά S όχι, τα τροχιακά P επηρεάζονται λιγότερο από τις διακυμάνσεις του κβαντικού κενού που προκύπτει από το ηλεκτρικό πεδίο του πυρήνα. Λόγω της διαφοράς μεταξύ των σχημάτων των δύο τροχιακών, το αποτέλεσμα είναι μια μετατόπιση του επιπέδου ενέργειας των δύο.

Εικ. 3. Ο Hans Bethe ήταν ο πρώτος που κατανόησε πώς μπορούμε να εξηγήσουμε τα άπειρα που προκύπτουν από την επέκταση της θεωρίας των διαταράξεων της QED. Η μέθοδός του, που ονομάζεται κανονικοποίηση, ισχύει για όλες τις επιτυχημένες σύγχρονες κβαντικές εξισώσεις. Πράγματι, αποτελεί πλέον απαίτηση για μια κβαντική θεωρία να είναι κανονικοποιημένη για να μπορεί να θεωρηθεί βιώσιμη.
Είναι ίσως συγκινητικό να γνωρίζουμε ότι ο Bethe επεξεργάστηκε τη λύση του, ενώ βρισκόταν σε βόλτα με το τρένο από τη Νέα Υόρκη για το Schenectady (περίπου 3,5 ώρες με τα σημερινά τρένα), αλλά αυτή είναι η φύση της μεγαλοφυίας. Αλλά η πραγματική ιδιοφυΐα του Bethe εμφανίζεται στο πώς θα λυθεί το θέμα των απείρων που προέκυψαν από τις κυματικές εξισώσεις Dirac δευτέρας τάξεως.
Για χρόνια, οι φυσικοί είχαν προσπαθήσει να υπολογίσουν τη μάζα του ηλεκτρονίου εν μέρει από τον υπολογισμό της αλληλεπίδρασής του με το περιβάλλον ηλεκτρικό πεδίο. Με τη χρήση της συμβατικής σχετικιστικής κβαντομηχανικής, το αποτέλεσμα είναι άπειρο. Αυτό που έκανε ο Bethe ήταν να ισχυριστεί ότι στην πραγματικότητα υπήρχαν δύο περιπτώσεις που έπρεπε να λαμβάνονται υπόψη, το δεσμευμένο από το άτομο ηλεκτρόνιο και το ελεύθερο ηλεκτρόνιο. Σε αμφότερες τις περιπτώσεις, η ίδιοενέργεια των ηλεκτρονίων υπήρχε, έτσι ο Bethe υποστήριξε ότι η μετρημένη μάζα του ελεύθερου ηλεκτρονίου ήδη περιείχε την ιδιοενέργεια από ένα ελεύθερο ηλεκτρόνιο. Επομένως, αντί να χρησιμοποιούν την υπολογισμένη τιμή (η οποία ήταν άπειρη) για το δεσμευμένο ηλεκτρόνιο, αυτή αντικαταστάθηκε με την μετρούμενη τιμή. Η τεχνική αυτή χρησιμοποιείται σήμερα ευρέως και ονομάζεται κανονικοποίηση. Έναν άλλο τρόπο που μπορούμε να σκεφτούμε γι αυτή την ενσωμάτωση είναι να περιοριστεί η μέγιστη δυνατή ενέργεια των φωτονίων ώστε να είναι η μάζα ηρεμίας του ηλεκτρονίου.
Η τεχνική της κανονικοποίησης είναι τώρα πιο κατανοητή από ό, τι ήταν όταν o Bethe την είχε γράψει στο ταξίδι με το τρένο. Ουσιαστικά αυτό που έχει γίνει είναι ότι η φυσική σε πολύ υψηλή ενέργεια δεν μπορεί να επηρεάσει τα χαμηλότερα ενεργειακά φαινόμενα που μπορούμε να μετρήσουμε τώρα. Από μαθηματική άποψη, αυτό αντιμετωπίζεται με την τοποθέτηση στην ενσωμάτωση μιας αποκοπής σε ανώτερο επίπεδο, αλλά εννοιολογικά περιλαμβάνει την αντικατάσταση των απείρων με φυσικά μετρούμενες παραμέτρους. Αν και αυτό φαίνεται λίγο σχηματικό (ο Richard Feynman [Εικ. 4] μάλιστα, ένας από τους πρώτους υποστηρικτές, το ονόμασε αγυρτεία), δεν είναι τόσο ανόητη όσο φαίνεται. Ένα πράγμα όμως είναι σχεδόν σίγουρα αλήθεια, ότι υπάρχουν ανεξερεύνητα φαινόμενα που συμβαίνουν σε υψηλότερες ενέργειες από όσα μπορούμε να ανιχνεύσουμε τώρα. Αυτό θα μπορούσε να είναι η υπερσυμμετρία, η κβαντική βαρύτητα ή κάτι που δεν έχουμε ακόμη φανταστεί. Όποιο και αν είναι, τιθασεύει τα άπειρα που προκύπτουν στη σημερινή ατελή θεωρία μας. Έτσι, ένας τρόπος για να σημειωθεί πρόοδος είναι να αποδεχθούμε τους περιορισμούς, να επιβάλλουμε όριο ολοκλήρωσης και να απορροφήσουμε την άγνοιά μας, αντικαθιστώντας τα μη φυσικά άπειρα με μετρημένες τιμές. Προφανώς μια βελτιωμένη θεωρία θα επιλύσει τα σημερινά μυστήρια. Λόγω αυτής της μαθηματικά περίεργης μεθοδολογίας, οι πρώτοι ερευνητές αυτού που τώρα ονομάζεται κβαντική ηλεκτροδυναμική (ή QED), είδαν την τεχνική τους ως εντελώς ανυπόληπτη, αλλά με πιο πρόσφατη έρευνα γι αυτό που σήμερα ονομάζουμε θεωρία κανονικοποιημένων ομάδων, έχει αποδειχθεί ότι είναι ο ακρογωνιαίος λίθος της σύγχρονων θεωριών. Πράγματι, για να θεωρείται επιτυχής μια σύγχρονη θεωρία πρέπει να είναι κανονικοποίησιμη (δηλαδή, να γράφεται έτσι ώστε να κρύβονται τα άπειρα και, εξίσου σημαντικό, για τον υπολογισμό να είναι ανεξάρτητη από οποιεσδήποτε αποκοπές επιλέξουμε στα ολοκληρώματα).
Κβαντική Ηλεκτροδυναμική (QED)

Εικ. 4. Ο Richard Feynman ήταν ένας από τους αρχιτέκτονες της σύγχρονης κβαντικής ηλεκτροδυναμικής. Απλουστεύοντας τα περίπλοκα μαθηματικά της QED με μια σειρά από διαισθητικές εικόνες, επέτρεψε γενιές φυσικών των σωματιδίων να κατανοήσουν την ουσία της επέκτασης της θεωρίας των διαταραχών.
Η προσέγγιση Bethe ήταν σαφώς μη σχετικιστική, αλλά γενικεύτηκε στους αναλλοίωτους μετασχηματισμούς Lorentz με μια σειρά μελετών από τους Αμερικανούς φυσικούς Richard Feynman και Julian Schwinger και τον Ιάπωνα φυσικό Sin-Itiro Tomonaga, οι οποίοι μοιράστηκαν το βραβείο Νόμπελ του 1965 στη Φυσική για την εργασία τους. Η τεχνική του Feynman βασίζεται σε μια σειρά από διαγράμματα και φαινόταν πολύ διαφορετική από το βαρύ φορμαλισμό των εξισώσεων του Schwinger και τουTomonaga, αλλά αποδείχθηκε από τον Βρετανό φυσικό Freeman Dyson ότι είναι ισοδύναμες. Λόγω του πιο διαισθητικού χαρακτήρα της προσέγγισης Feynman, περιορίζουμε τη συζήτηση εδώ σε αυτή τη μεθοδολογία.
Και οι τρεις προσεγγίσεις χρησιμοποίησαν τη θεωρία των διαταραχών για την εκτέλεση υπολογισμών της QED. Η λαμπρότητα του Feynman έγκειται στο γεγονός ότι είναι σε θέση να κάνει κβαντικούς ηλεκτροδυναμικούς υπολογισμούς με μια σειρά από εικόνες. Οι εικόνες αντιπροσωπεύουν τους επιμέρους όρους της διάδοσης των διαταραχών. Κάθε εικόνα μπορεί να μετατραπεί σε μια εξίσωση.
Η διάδοση των διαταραχών μπορεί να γίνει κατανοητή ως μια σειρά ολοένα και πιο πολύπλοκων αλληλεπιδράσεων. Όταν ένα ηλεκτρόνιο σκεδάζεται από ένα άλλο, καθώς τα δύο ηλεκτρόνια περνούν το ένα δίπλα από το άλλο, μπορούν να προκύψουν πολλές διαφορετικές αλληλεπιδράσεις. Ωστόσο, οι αλληλεπιδράσεις κατατάσσονται από το αριθμητικό μέγεθος της συνεισφοράς τους στην τελική απάντηση. Για παράδειγμα, ο μεγαλύτερος όρος στην επέκταση πραγματοποιείται όταν ένα ηλεκτρόνιο εκπέμπει ένα ενιαίο φωτόνιο που απορροφάται από το άλλο ηλεκτρόνιο και τα δύο ηλεκτρόνια ανακρούονται. Ένα λιγότερο πιθανό σενάριο είναι ότι ένα από τα εισερχόμενα ή εξερχόμενα ηλεκτρόνια μπορεί να εκπέμψει ένα δικό του φωτόνιο. Ακόμη λιγότερο πιθανό είναι να εκπεμφθούν δύο φωτόνια. Υπάρχουν άπειρα επίπεδα αυξανόμενου αριθμού εκπεμπόμενων φωτονίων στην σκέδαση. Η Εικ. 5 απεικονίζει τις πρώτες δυνατότητες.
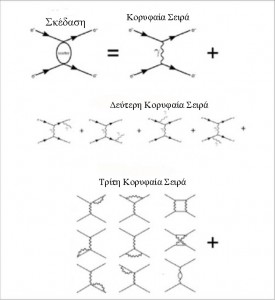
Εικ. 5.Η σκέδαση των δύο πραγματικών ηλεκτρονίων μπορεί να προσεγγιστεί ως μια σειρά ολοένα και πιο πολύπλοκων σχημάτων εκπομπών. Πραγματοποιώντας τον υπολογισμό με τον τρόπο αυτό, μπορεί κανείς να χρησιμοποιήσει τη θεωρία των διαταραχών για την προσέγγιση του υπολογισμού και ο υπολογισμός μπορεί να γίνει σε ένα αυθαίρετο επίπεδο ακρίβειας, συμπεριλαμβάνοντας τον απαιτούμενο αριθμό όρων. Η σχετική μεταβλητή επέκταση καθορίζεται από τον αριθμό των κορυφών με την απορρόφηση ή εκπομπή ενός φωτονίου, π.χ., δύο στην κορυφαία σειρά, τρεις στην δεύτερη κύρια σειρά, τέσσερις στην τρίτη κύρια σειρά, και ούτω καθεξής.
Ανώμαλη μαγνητική ροπή
Η QED μπορεί και να έχει ελεγχθεί καλύτερα από οποιαδήποτε άλλη θεωρία που έχει επινοηθεί. Ίσως η πιο επιτυχημένη σύγκριση των μετρήσεων και της θεωρητικής πρόβλεψης είναι η μαγνητική ροπή του ηλεκτρονίου, η οποία φτάνει σε ακρίβεια του ενός προς ένα τρισεκατομμύριο. Ενώ υπάρχουν πολλές πειραματικές προσεγγίσεις για την μέτρηση αυτής της ποσότητας, ίσως το πιο εύκολο είναι να ρίξεις ένα ηλεκτρόνιο μέσα σε ένα μαγνητικό πεδίο. Επειδή το ηλεκτρόνιο είναι ηλεκτρικά φορτισμένο και έχει κβαντικό μηχανικό σπιν, ουσιαστικά είναι ένας μικρός μαγνήτης με δική του μαγνητική ροπή. Η μαγνητική ροπή σε ένα μαγνητικό πεδίο θα αισθανθεί μια άλλη ροπή και θα υπάρξει μετάπτωση γύρω από την κατεύθυνση του μαγνητικού πεδίου. Μια μέτρηση της μαγνητικής ροπής του ηλεκτρονίου παρουσιάστηκε για πρώτη φορά από τον Γερμανικής καταγωγής Αμερικανό φυσικό Polykarp Kusch την εποχή που γινόταν το επιστημονικό συνέδριο του 1947 κατά την οποίο η ανακοίνωση της μετατόπισης Lamb δημιούργησε όλη αυτή την αναστάτωση.
Με τη μέτρηση της συχνότητας μετάπτωσης του ηλεκτρονίου, μπορεί κανείς να εξάγει πειραματικά τη μαγνητική ροπή του. Η θεωρητική μαγνητική ροπή του ηλεκτρονίου μπορεί να προβλεφθεί χρησιμοποιώντας την εξίσωση Dirac και βρέθηκε να είναι
![]()
όπου s είναι το σπιν των ηλεκτρονίων, είναι ℏ η σταθερά του Πλανκ διαιρούμενη δια 2π, μΒ είναι η μαγνητική ροπή Bohr, και g είναι ο συντελεστής g του ηλεκτρονίου, ο οποίος προβλέπεται από τη θεωρία του Dirac να είναι παντού 2 . Ο Kusch και οι πνευματικοί απόγονοί του διαπίστωσαν αρχικά ότι η μετρούμενη μαγνητική ροπή διαφέρει από την πρόβλεψη του Dirac κατά περίπου 0,1%. Ο Julian Schwinger μπόρεσε να υπολογίσει πρώτος τη διαφορά αυτή, το 1948, χρησιμοποιώντας τη QED. Αποδείχτηκε ότι οι επιδράσεις της QED μπορούν να αλλάξουν διακριτικά την μαγνητική ροπή του απλού ηλεκτρονίου Dirac, επειδή το ηλεκτρόνια συνεχώς εκπέμπουν και επαναπορροφούν φωτόνια. Όταν ο Schwinger έλαβε υπόψη τη χαμηλότερη σειρά προσέγγισης της αυτο-αλληλεπίδρασης των ηλεκτρονίων, που ονομάζεται χαμηλότερης τάξης διάγραμμα βρόχου και φαίνεται στο Εικ. 6, θα μπορούσε να εξηγήσει τη διαφορά μεταξύ της πρόβλεψης και της μέτρησης. Η εξέλιξη της τεχνολογίας έχει βελτιωθεί με την πάροδο των δεκαετιών και μπορούμε να γράψουμε την πειραματική μέτρηση ίση με:
gμετρούμενη = 2,00231930436146 ± 0,00000000000048,
με προβλεπόμενη τιμή (χρησιμοποιώντας τη 10η σειρά θεωρίας διαταραχών)
gπροβλεπόμενη = 2,00231930436356 ± 0.0000000000011,
με gμετρούμενη – gπροβλεπόμενη = (-1,05 ± 0,82)x10-12. Αυτή η συμφωνία μεταξύ θεωρίας και πειράματος είναι από τις καλύτερες που έχει επιτευχθεί ποτέ και θεωρείται μια ηχηρή υποστήριξη για τη θεωρία της QED.
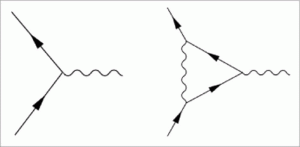
Εικ. 6. Η μικρή διαφωνία μεταξύ των μετρήσεων και της πρόβλεψη του Dirac για τη μαγνητική ροπή του ηλεκτρονίου εξηγήθηκε χρησιμοποιώντας διορθώσεις της QED. Όταν ένα ηλεκτρόνιο σκεδάζεται από ένα φωτόνιο (αριστερά), πρέπει κανείς να εξετάσει την επίδραση του ηλεκτρονίου πρώτα εκπέμποντας ένα φωτόνιο, το οποίο στη συνέχεια αργότερα επαναπορροφάται (δεξιά). Αυτό το διάγραμμα “βρόχου” είναι η κυρίαρχη συμβολή στην απόκλιση του 0,1%.
Εννοιολογική κβαντική θεωρία πεδίου
Ενώ υπήρξε θεαματική επιτυχία της θεωρίας της QED, είναι αρκετά εύκολο να αφήσεις μια συζήτηση των διαγραμμάτων Feynman και τους υπολογισμούς ακριβείας, χωρίς μια θεμελιώδη διαίσθηση για το τι ακριβώς είναι ένα ηλεκτρόνιο. Έτσι επιστρέφουμε τώρα σε μια πιο ολιστική συζήτηση. Η QED είναι ένα συγκεκριμένο παράδειγμα του τι λέγεται κβαντική θεωρία πεδίου ή QFT.
Στην ουσία, σε μια QFT, η ύλη όπως εμείς συνήθως τη σκεφτόμαστε, δεν υπάρχει. Δεν υπάρχει κομμάτι της ύλης που είναι ηλεκτρόνιο ή, για αυτή την ύλη, φωτόνιο, κουάρκ ή οποιαδήποτε άλλα θεμελιώδη σωματίδια. Αντ’ αυτού, ολόκληρο το σύμπαν είναι γεμάτο με πεδία -πεδία ηλεκτρονίων, πεδία κουάρκ, πεδία φωτονίων – ένα πεδίο για κάθε τύπο θεμελιώδους (δηλαδή, σημειακού) σωματιδίου που υπάρχει.
Όταν ένα πεδίο είναι αδρανές, ουσιαστικά τίποτα δεν συμβαίνει. Ωστόσο, αυτά τα πεδία μπορεί να υποστηρίξουν κβαντισμένες δονήσεις. Μια κβαντισμένη δόνηση είναι μια εντοπισμένη δόνηση-αυτό που έχει ονομαστεί πακέτο κυμάτων ή κυματοσυρμός στις περιγραφές της κβαντομηχανικής του 1920. Και κάθε κβαντισμένη δόνηση του πεδίου ηλεκτρονίων είναι η φυσική εμφάνιση ενός ηλεκτρονίου.
Τα διαφορετικά πεδία μπορεί μερικές φορές να αλληλεπιδρούν μεταξύ τους. Για παράδειγμα, όταν ένα ηλεκτρόνιο εκπέμπει ένα φωτόνιο, μια κλασσική περιγραφή θα μπορούσε να είναι μια μικρή μπάλα που μοιάζει με ηλεκτρόνιο που κινείται σε μία γραμμή και εκπέμπει ένα φωτόνιο, το οποίο, ανάλογα με την ψυχοσύνθεσή σας, μπορείτε να φανταστείτε ως μια μπάλα (π.χ., το φωτοηλεκτρικό φαινόμενο) ή μικρό πακέτο κυμάτων (π.χ., θεωρία των κυμάτων). Ωστόσο, η εικόνα αυτή είναι μία αναλογία στο παράδειγμα της QFT.
Στο παράδειγμα της QFT, ένα ηλεκτρόνιο είναι μια εντοπισμένη δόνηση του πεδίου ηλεκτρονίων. Στο σημείο της εκπομπής, το πεδίο των ηλεκτρονίων και το πεδίο των φωτονίων αλληλεπιδρούν και δημιουργείται μία εντοπισμένη δόνηση στο πεδίο των φωτονίων. Η δόνηση των φωτονίων τρέχει με την ταχύτητα του φωτός, ενώ το ηλεκτρόνιο συνεχίζει στο πεδίο των ηλεκτρονίων, με αλλαγή της διεύθυνσή του, του μήκους κύματος και τηςταχύτητας. Η αλληλεπίδραση μεταξύ των δύο πεδίων είναι παρόμοια με τη συμπεριφορά συντονισμού δύο γειτονικών διαπασών. Αν δονήσετε ένα διαπασών, το άλλο διαπασών θα δονείται επίσης.
Και αυτή η απλή εικόνα των δονούμενων παδίων ισχύει για όλα τα θεμελιώδη σωματίδια: τα κουάρκ και τα λεπτόνια καθώς και τα μποζόνια που μεταφέρουν δύναμη. Αυτό δεν ισχύει για τα σύνθετα σωματίδια, όπως τα πρωτόνια και τα νετρόνια και για όλο το πλήθος των μεσονίων και των βαρυονίων που έχουμε ανακαλύψει. Ή, ακριβέστερα, για να περιγράψει ένα σύνθετο σωματίδιο, θα πρέπει να εξετάσουμε τις (συχνά οποίες αλληλεπιδρούν μεταξύ τους) δονήσεις όλων των πεδίων των συστατικών τους σωματιδίων.
Κοντά στο ηλεκτρόνιο
Κοντά σε ένα ηλεκτρόνιο, τα πράγματα είναι περίπλοκα. Λέγεται συχνά ότι ένα ηλεκτρόνιο είναι ένα σημειακό σωματίδιο, πράγμα που σημαίνει ότι έχει μηδενικό μέγεθος. Αυτό είναι αλήθεια, τουλάχιστον μέσα στα πλαίσια της σύγχρονης πειραματικής ανάλυσης, η οποία θέτει το άνω όριο στο μέγεθος του ηλεκτρονίου στα 2 × 10-20 μέτρα. Δεδομένου ότι τόσο (α) η QED αξιώνει ότι το μέγεθος του ηλεκτρονίου είναι μηδέν όσο και (β) ότι τα στοιχεία είναι συνεπή με το εν λόγω αξίωμα, μπορεί κανείς να περιγράψει αυτό που “μοιάζει με” ένα ηλεκτρόνιο με την παραδοχή του μηδενικού μεγέθους. Θα δούμε ότι η ακριβής έννοια του όρου “μηδενικό μέγεθος” είναι λεπτή.
Στην απλούστερη κλασική εικόνα, η έννοια είναι σαφής. Το ηλεκτρόνιο έχει πραγματικά μηδενικό μέγεθος και περιβάλλεται με ένα ηλεκτροστατικό δυναμικό που περιγράφεται από τη σχέση V = -ke / r. Μια πιο εξελιγμένη κλασσική ανάλυση του ηλεκτρονίου δίδει ένα μέγεθος που ονομάζεται κλασική ακτίνα του ηλεκτρονίου, της τάξης των 10-15 m, το οποίο είναι απλά το μέγεθος μιας σφαίρας με το φορτίο του ηλεκτρονίου και με την ενέργεια που απαιτείται για να συγκεντρωθεί αυτό, που είναι ίση με την μάζα της ενέργειας του ηλεκτρονίου.
Ωστόσο, στο μοντέλο της QFT, ενώ υπάρχει ένα “γυμνό” ηλεκτρόνιο με μηδενικό μέγεθος στο κέντρο του ηλεκτρονίου, αυτό περιβάλλεται από ένα νέφος φωτονίων και ζευγών ηλεκτρονίου / ποζιτρονίου. Αυτά τα σωματίδια είναι συνήθως εικονικά, πράγμα που σημαίνει ότι δεν έχουν τη “σωστή” μάζα, δηλαδή τη μάζα που έχει να κάνει με τα ελεύθερα σωματίδια. Πιο συγκεκριμένα αυτό σημαίνει ότι αυτά τα φωτόνια δεν είναι άμαζα και τα ηλεκτρόνια και ποζιτρόνια δεν έχουν μάζα 0.511 MeV / c2(σ.μ. είναι η συνήθης μάζα του ηλεκρονίου/ποζοτρονίου). Μπορούν να υπάρχουν επειδή η αρχή της αβεβαιότητας του Heisenberg επιτρέπει την ύπαρξη σωματιδίων με “λάθος” μάζα, εάν δεν υπάρχουν για πολύ χρόνο.
Η δίνη των εικονικών σωματιδίων γίνεται όλο και πιο ξέφρενη καθώς πηγαίνουμε πιο κοντά στον πυρήνα του ηλεκτρονίου. Με όρους της QFT, αυτό σημαίνει απλά ότι το “γυμνό” ηλεκτρικό φορτίο διαταράσσει το πεδίο των φωτονίων, το οποίο με τη σειρά του διαταράσσει το πεδίο των ηλεκτρονίων. Το καθαρό αποτέλεσμα είναι ένα περίπλοκο χάος και με το “γυμνό” φορτίο να προστατεύεται από το περιβάλλον νέφος των εικονικών σωματιδίων. Σημαίνει, επίσης, ότι το ενεργό φορτίο του ηλεκτρονίου αλλάζει με την ενέργεια με την οποία το τροφοδοτείς. Όπως όταν βάλεις ένα σωματίδιο προς ένα ηλεκτρόνιο, υψηλότερης ενέργειας βολές μπορούν να διεισδύσουν βαθύτερα στο σύννεφο, οπότε βλέπεις περισσότερα “γυμνά” φορτία και έχεις την εμπειρία περισσότερων αποτελεσμάτων εικονικών σωματιδίων. Έτσι, το ηλεκτρόνιο δεν είναι πλέον απλώς ένα γυμνό φορτίο. Έχει μια περίπλοκη ακτινική κατανομή φορτίου. Αν κάποιος επιθυμεί να βρει την ενέργειά του σε ένα άτομο σε ένα συγκεκριμένο επίπεδο ενέργειας, πρέπει να ενσωματώσει πάνω στην κατανομή της θέσης του και το ηλεκτρικό πεδίο που επιδρά από τον πυρήνα. Ο συνδυασμός των διαφορετικών σχημάτων των S και Ρ τροχιακών, σε συνδυασμό με αυτή τη μικρή κατανομή φορτίου του ηλεκτρονίου, είναι η βάση της μετατόπισης Lamb. Μια συμπληρωματική δράση προκύπτει από μία όμοια επεξεργασία του ηλεκτρικού πεδίου στη γειτονιά του πυρήνα.
Αυτή η τροποποίηση του φορτίου του ηλεκτρονίου λόγω αύξηση της ενεργειακής στάθμης, έχει επαληθευθεί πειραματικά με πολύ καλή ακρίβεια. Δεν υπάρχει καμία ένδειξη ότι το θεωρητικό ηλεκτρόνιο στον πυρήνα της καταιγίδας των φωτονίων και των εικονικών σωματιδίων αποτελείται από μικρότερα αντικείμενα. (Σημειώστε ότι ξεχωρίζουμε το θεωρητικό σωματίδιο από το φυσικό ηλεκτρόνιο.) Εν εξελίξει μετρήσεις συνεχίζουν να αναζητούν ενδείξεις που να μας δείχνουν ότι ο πυρήνας των ηλεκτρονίων θα μπορούσε να αποτελείται από ακόμη μικρότερα συστατικά. Μέχρι στιγμής, όλες οι προσπάθειες για τον εντοπισμό συστατικών των ηλεκτρονίων έχουν αποτύχει.
Μυστήρια που Παραμένουν
Ενώ είναι αλήθεια ότι η θεωρία της QED είναι η πιο ακριβής που επινοήθηκε ποτέ, ακόμη και σήμερα μερικά μυστήρια παραμένουν. Για παράδειγμα, δύο παράμετροι της θεωρίας της QED που δεν μπορούν να υπολογιστούν με τις πρώτες αρχές, είναι η μάζα και το ηλεκτρικό φορτίο του ηλεκτρονίου. Αυτές οι παράμετροι πρέπει να προσδιορίζονται εμπειρικά και να επανέλθουμε στη θεωρία με το χέρι. Αυτό είναι ένα σαφές μήνυμα ότι η QED δεν είναι η τελευταία λέξη, αλλά μάλλον είναι ένα αποτελεσματικό μοντέλο που προκύπτει από μια βαθύτερη και πιο θεμελιώδη θεωρία.
Αλλά αν αρχίσουμε να σκεφτόμαστε πιο ελεύθερα, οι ερωτήσεις δεν σταματούν εκεί. Ιδού μερικά μόνο ερωτήματα για τα οποία δεν γνωρίζουμε τις απαντήσεις. Γιατί τα ηλεκτρόνια μεταφέρουν ηλεκτρικό φορτίο, αλλά όχι το ισχυρό πυρηνικό φορτίο; Τι είναι αυτό που διακρίνει το ηλεκτρόνιο από τα ξαδέλφια του, το μιόνιο και ταυ λεπτόνιο (εκτός της προφανούς απάντησης της μάζας); Γιατί το ηλεκτρόνιο και το πρωτόνιο έχουν ακριβώς την ίδια ποσότητα ηλεκτρικού φορτίου, μέχρι ενός σημείου; Τι συμβαίνει όταν η κυματοσυνάρτηση των ηλεκτρονίων καταρρέει και εντοπίζεται το ηλεκτρόνιο; Μήπως τελικά τα ηλεκτρόνια έχουν συστατικά; Ερωτήσεις χωρίς απαντήσεις είναι κοινές για τους ερευνητές και το μόνο που σημαίνουν είναι ότι το ταξίδι μας να κατανοήσουμε το ηλεκτρόνιο δεν έχει ολοκληρωθεί ακόμη.
Σύνοψη
Όπως γνωρίζουμε εδώ και σχεδόν έναν αιώνα, ο υποατομικός κόσμος είναι ένας αντιφατικός κόσμος, όπου η σωματιδιακή και κυματική συμπεριφορά παίζουν ένα σημαντικό ρόλο. Ωστόσο, γνωρίζουμε ότι το ηλεκτρόνιο δεν είναι ένα κλασικό σωματίδιο ούτε ένα κλασικό κύμα. Είναι κάτι που περιγράφτηκε από την κβαντομηχανική της δεκαετίας του 1920 με την ιδέα του “πακέτου κύματος”, αλλά η πραγματικότητα είναι πιο σύνθετη και θα πρέπει πραγματικά να θεωρηθεί ως ένα συνεχώς μεταβαλλόμενο πλέγμα αλληλεπιδρόντων πεδίων. Η κβαντική ηλεκτροδυναμική (QED) είναι μια θεωρία που περιγράφει τη συμπεριφορά και τις θεμελιώδεις ιδιότητες του ηλεκτρονίου με εκπληκτική ακρίβεια. Η σύγχρονη εικόνα του ηλεκτρονίου είναι πολύπλοκη, αποτελούμενη από δονήσεις ενός βασικού ηλεκτρονιακού πεδίου, που περιβάλλεται από ένα εξίσου δονούμενο πεδίο φωτονίων καθώς και με τις δονήσεις πεδίων άλλων θεμελιωδών υποατομικών σωματιδίων. Η όμορφη ακρίβεια των προβλέψεων της QED εξασφαλίζει ότι η εικόνα αυτή θα συνεχιστεί. Ωστόσο, καμία θεωρία δεν είναι για πάντα. Ποιο θα είναι το όραμά μας για το ηλεκτρόνιο ένα αιώνα από τώρα;
Γιάννης Γαϊσίδης

Εξαιρετική δουλειά για την εκλαικευση των πιο πρόσφατων γνώσεων της κβαντικής Ηλεκτροδυναμικής. Μπράβο σας!
Ευχαριστώ για το ενδιαφέρον σου Δημήτρη.