The Physics Teacher
By Asif Shakur, Salisbury University, Maryland US

Το παρακάτω άρθρο αναφέρεται σε ένα ενδιαφέρον πρόβλημα, με το οποίο μπορούν να ασχοληθούν οι μαθητές της Γ΄ Λυκείου, που επιθυμούν να εμπεδώσουν τις γνώσεις τους πάνω στις αρχές της διατήρησης της Ορμής και της Ενέργειας καθώς και στην περιστροφή στερεού σώματος. Δίνει όμως το έναυσμα και σε εκπαιδευτικούς να προχωρήσουν στη σύνθεση ερωτημάτων προς τους μαθητές τους σχετικά με την εφαρμογή των αρχών της διατήρησης.

Βίντεο 1: Οι δύο ξύλινες δοκοί χτυπιούνται σε διαφορετικά σημεία. Η μία κατ’ ευθείαν στο κέντρο της (η δοκός δεν περιστρέφεται) και η άλλη εκτός κέντρου (η δοκός περιστρέφεται). Ποια δοκός ανεβαίνει ψηλότερα;

Βίντεο 2: Η απάντηση. Και οι δύο φτάνουν στο ίδιο ύψος. Γιατί;

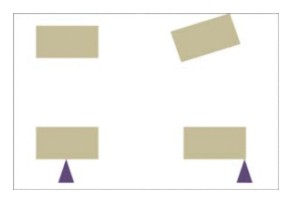
Η επιστημονική μελέτη του βίντεο της δοκού που βάλλεται από μία σφαίρα, δείχνει μια ξύλινη δοκό, η οποία βάλλεται από ένα κάθετο προς το στόχο τουφέκι. Το βίντεο δείχνει ότι η δοκός που χτυπήθηκε κατ’ ευθείαν στο κέντρο πηγαίνει ακριβώς τόσο υψηλό όσο θα πήγαινε αν τη χτυπούσαμε εκτός κέντρου(έκκεντρα). (Εικ. 1). Το πρόβλημα είναι ότι η δοκός που κτυπήθηκε εκτός κέντρου μεταφέρει, εκτός από την βαρυτική δυναμική ενέργεια και περιστροφική κινητική ενέργεια. Αυτό οδηγεί την πλειοψηφία των bloggers να ισχυριστεί ότι η δοκός που πυροβολήθηκε εκτός κέντρου δεν πρέπει να πάει τόσο ψηλά όσο αυτή που πυροβολήθηκε στο κέντρο. Άλλοι έχουν υποστηρίξει ότι η ενέργεια που συνδέεται με την περιστροφή είναι ασήμαντη και οι δύο περιπτώσεις και η δοκός θα πρέπει να ανεβεί στο ίδιο ύψος μέσα στα όρια του πειραματικού σφάλματος.

Το παρόν άρθρο εξετάζει τους εντυπωσιακούς ισχυρισμούς και παρέχει μια σαφή λύση στο γρίφο. Η σωστή βασική αρχή που ισχύει σε αυτή την σύγκρουση είναι η αρχή της διατήρησης της ορμής. Η σύγκρουση είναι ανελαστική (“πλαστική”), επειδή η σφαίρα ενσωματώνεται στη ξύλινη δοκό. Η μηχανική ενέργεια (δυναμική και κινητική) δεν διατηρείται στις ανελαστικές συγκρούσεις. Έστω ότι η μάζα του βλήματος είναι m και η μάζα της δοκού είναι M. Τότε η διατήρηση της γραμμικής ορμής κατά την κατακόρυφη κατεύθυνση σημαίνει ότι η αρχική γραμμική ορμή του βλήματος είναι ίση με την τελική γραμμική ορμή του συσσωματώματος σφαίρα-δοκός.

(1) $\begin{equation*} mv_{\alpha \rho \chi}=(m+M)v_{\tau \epsilon \lambda} \end{equation*}$

(2) $\begin{equation*} v_{\tau \epsilon \lambda}=\frac{m}{m+M}v_{\alpha \rho \chi} \end{equation*}$

Η σφαίρα κτυπά τη μία ξύλινη δοκό στο κέντρο και η άλλη εκτός κέντρου

Εικ. 1. Η σφαίρα κτυπά τη μία ξύλινη δοκό στο κέντρο και την άλλη εκτός κέντρου

Έτσι, η τελική ταχύτητα του συσσωματώματος αμέσως μετά το κτύπημα της σφαίρας δεν εξαρτάται καθόλου από το αν το μπλοκ περιστρέφεται ή όχι καθώς ανεβαίνει.Το κέντρο μάζας της δοκού που χτυπήθηκε κατ’ ευθείαν στο κέντρο της θα ανεβεί προς επάνω στο ίδιο ύψος με το κέντρο μάζας της δοκού που χτυπήθηκε εκτός κέντρου και περιστρέφεται καθώς ανεβαίνει.

Μια λανθασμένη αρχή διατήρηρης

Εκείνοι που ισχυρίζονται ότι η περιστρεφόμενη δοκός δεν θα πρέπει να ανεβεί στο ίδιο ύψος, φαίνεται να εφαρμόζουν λανθασμένα το νόμο τη διατήρηση. Προφανώς, πιστεύουν ότι το συνολικό ποσό της βαρυτικής δυναμικής ενέργειας και της περιστροφικής κινητικής ενέργειας πρέπει να διατηρηθεί. Δεδομένου ότι η περιστρεφόμενη δοκός έχει κάποια περιστροφική κινητική ενέργεια, θα έχει, κατά συνέπεια, μικρότερη βαρυτική δυναμική ενέργεια και άρα δε θα πρέπει να έρθει στο ίδιο ύψος με τη δοκό που χτυπήθηκε στο κέντρο της και δεν περιστρέφεται. Τα σαθρά θεμέλια επί των οποίων λανθασμένα βασίζεται αυτός ο ισχυρισμός, φαίνεται να οφείλονται σε μία άλλη λανθασμένη αντίληψη του νόμου της διατήρησης, που μπορεί να διακριθεί σε δύο μέρη.

(α) Η συνολική κινητική ενέργεια της σφαίρας μεταφέρεται στη δοκό και δίνει τη συνολική κινητική της ενέργεια.
(β) Ακόμα και αν το (α) δεν είναι αληθές, τουλάχιστον το ίδιο κλάσμα της συνολικής κινητικής ενέργειας της σφαίρας μεταφέρεται ως συνολική ενέργεια (βαρυτική δυναμική ενέργεια και περιστροφική κινητική ενέργεια) της δοκού, αν λάβουμε υπόψη την περιστροφή της.

Κατάρριψη του λανθασμένου ισχυρισμού για το νόμο της διατήρησης (α)

Ας απορρίψουμε πρώτα γρήγορα και συνοπτικά το λάθος στο νόμο της διατήρησης (α). Η σφαίρα χάνει σχεδόν το σύνολο της κινητικής της ενέργειας είτε συμπιέζοντας το ξύλο ή κατά την τριβή μ’ αυτό και την παραγωγή θερμότητας, καθώς ενσωματώνεται στη δοκό. Μόνο μια ασήμαντη ποσότητα της αρχικής κινητικής ενέργειας της σφαίρας μεταφέρεται ως κινητική ενέργεια της δοκού ανεξάρτητα από το αν περιστρέφεται ή όχι.

Αυτό μπορεί να αποδειχθεί σημειώνοντας ότι ο λόγος της μεταφερόμενης κινητικής ενέργειας του συσσωματώματος σφαίρα – δοκός προς την αρχική κινητική ενέργεια του βλήματος είναι:

(3) $\begin{equation*} \lambda =\frac{\frac{1}{2}(m+M)(v_{\tau \epsilon \lambda})^2}{\frac{1}{2}m(v_{\alpha \rho \chi})^2}} \end{equation*}$

Αντικαθιστώντας στην (3) τη $v_{\tau \epsilon \lambda}$ από τη (2) και απλοποιώντας έχουμε:

(4) $\begin{equation*} \lambda =\frac{m}{m+M} \end{equation*}$

Ας εξετάσουμε ένα συγκεκριμένο παράδειγμα: Μία σφαίρα των 20gr με ταχύτητα 400 m / s έχει μια αρχική κινητική ενέργεια $K=\frac{1}{2}mv^2=1600 J$ . Είτε η βολή γίνεται κατ’ ευθείαν στο κέντρο (χωρίς περιστροφή) ή εκτός κέντρου (περιστροφή) πάνω σε ξύλινη δοκό διαστάσεων 20 cm × 10 cm × 10 cm, που έχει μάζα 1,4 kg, το 98,6% της αρχικής κινητικής ενέργειας της σφαίρας δε μεταφέρεται στη δοκό ως μεταφορική κινητική ενέργεια.Το συσσωμάτωμα δοκός-βλήμα λαμβάνει μόνο 23 J από τα αρχικού 1600J ως μεταφορική κινητική ενέργεια, Αυτό προκύπτει αν αντικαταστήσουμε τις τιμές των μαζών στην (4) και κατόπιν υπολογίσουμε την ΚΕ του συσσωματώματος:

$\lambda=\frac{0,02kg}{0,02kg+1,4kg}=0,014$

και

$KE_{\sigma v \sigma}=0,014 \cdot 1600J=23J$

Αυτή μετατρέπεται σε βαρυτική δυναμική ενέργεια (ΔΕ) καθώς ανεβαίνει η δοκός σε ύψος μόνο 1,6 .

$\Delta E=KE \Leftrightarrow h=\frac{KE}{(m+M)g}=\frac{23J}{1,42kg \cdot 9,8m/s^2}=1,6m$

Για να βάλουμε τα πράγματα σε μια προοπτική, αν όλη η αρχική ΚΕ του βλήματος μετατραπεί σε βαρυτική ΔΕ, η δοκός θα ανέλθει σε ύψος 114m!

Κατάρριψη του λανθασμένου ισχυρισμού για το νόμο της διατήρησης (β)

Η δοκός περιστρέφεται επειδή χτυπιέται από τη σφαίρα εκτός κέντρου (έκκεντρα). Ας εφαρμόσουμε τη διατήρηση της στροφορμής στη δοκό. Αν η δοκός χτυπηθεί έκκεντρα στην άκρη του μπλοκ, η στροφορμή της σφαίρας ως προς άξονα που διέρχεται από το κέντρο της μάζας της δοκού πρέπει να είναι ίση με το στροφορμή της περιστρεφόμενης δοκού.

(5) $\begin{equation*} mdv_{\alpha \rho \chi}=I \omega \end{equation*}$

Χρησιμοποιώντας για την περίπτωσή μας τις τιμές d=0,1m και $I=5,8x10^{-3}kg \cdot m^2$ παίρνουμε:

$\omega=138rad/s$

Και η τιμή αυτή αντιστοιχεί σε κινητική ενέργεια λόγω περιστροφής της δοκού

$\frac{1}{2}I \omega^2=55J$

Επομένως η περιστρεφόμενη δοκός λαμβάνει ένα μεγαλύτερο κλάσμα της αρχικής κινητικής ενέργειας του βλήματος με τη μορφή της μηχανικής ενέργειας (μεταφορική και περιστροφική κινητική ενέργεια). Λαμβάνει όμως την ίδια μεταφορική κινητική ενέργεια (23J), όπως η μη περιστρεφόμενη δοκός. Το γεγονός αυτό εξηγεί γιατί και στις δύο περιπτώσεις έχουμε άνοδο στο ίδιο ύψος ύψος. Eπιπλέον όμως, λαμβάνει επίσης κάποια περιστροφική κινητική ενέργεια. Στην πραγματικότητα, στο παράδειγμά μας, η περιστροφική ΚΕ είναι περισσότερο από δύο φορές η μεταφορική ΚΕ! Έτσι, δεν μπορεί κανείς να ισχυριστεί το “περίπου αληθινό συμπέρασμα” ότι η κινητική ενέργεια περιστροφής είναι ασήμαντη σε σύγκριση με τη μεταφορική κινητική ενέργεια. Εκείνο που είναι σίγουρα σωστό είναι ότι και σ’ αυτή την περίπτωση η μορφή αυτή της κινητικής ενέργειας είναι ασήμαντη σε σύγκριση με την αρχική κινητική ενέργεια του βλήματος.

Σε ποια κατηγορία έχει η σφαίρα διεισδύει βαθύτερα;

Η παραπάνω ανάλυση δείχνει ότι η περιστρεφόμενη δοκός κερδίζει περισσότερη κινητική ενέργεια από τη σφαίρα από ό, τι η μη περιστρεφόμενη. Η σφαίρα διαθέτει μεγαλύτερο μέρος από την αρχική κινητική της ενέργεια για να διεισδύσει στη μη περιστρεφόμενη δοκό. Πρέπει επομένως να διεισδύει βαθύτερα στη μη περιστρεφόμενη δοκό. Αλλά είναι εύκολα μετρήσιμη αυτή η διαφορά; Η απάντηση είναι όχι. Σκεφτείτε ότι στο παράδειγμά μας παραπάνω, η σφαίρα είχε συνολική ΚΕ 1600 J. Η ΚΕ της μη περιστρεφόμενης δοκού είναι 23 J. Αυτό αφήνει ένα σημαντικό πόσο 1.577 J για να διεισδύσει μέσα στη δοκό. Στην περίπτωση της περιστρεφόμενης δοκού, η συνολική ΚΕ είναι 78 J (23J+55J), αφήνοντας 1,522 J για να διεισδύσει. Η διαφορά του 4% στο μήκος της οπής που ανοίγει η σφαίρα είναι σχεδόν αδύνατο να γίνει διακριτή. Παρεμπιπτόντως, το online βίντεο κάνει κάποιες αντιφατικές δηλώσεις από την άποψη αυτή. Στην αρχή, οι ερευνητές κεντούν τις τρύπες με ένα καρφί και βλέπουμε μεγάλη διαφορά στις τρύπες. Η τρύπα του περιστρεφόμενου φαίνεται να είναι πολύ μικρότερη. Στη συνέχεια, κάνουν πίσω και συνειδητοποιούν ότι η διαφορά δεν είναι τόσο εύκολα μετρήσιμη. Ο λόγος για αυτήν την απόκλιση είναι ότι η τρύπα στη περιστρεφόμενη δοκό είναι κυρτή. Σπρώχνοντας ένα καρφί μέσα σε αυτή τη δοκό θα δείχνει ότι η τρύπα είναι πολύ μικρή. Μια εικόνα με ακτίνες x είναι αυτό που τελικά μας δείχνει το σωστό.

Συμπέρασμα

Μία ξύλινη δοκός θα ανέλθει στο ίδιο ύψος, αν η σφαίρα τη χτυπά στο κέντρο της και δεν τη θέτει σε περιστροφήι, με τη δοκό την οποία χτυπά έκκεντρα και τη περιστρέφει. Αυτό προκύπτει από την αρχή της διατήρησης της γραμμικής ορμής. Η κινητική ενέργεια του συσσωματώματος δοκός-σφαίρα μετά την σύγκρουση είναι μόνο ένα ασήμαντο κλάσμα της αρχικής κινητικής ενέργεια της σφαίρας. Το μεγαλύτερο μέρος της αρχικής κινητικής ενέργειας καταναλώνεται είτε στη συμπίεση του ξύλου είτε στο έργο από την τριβή και παραγωγή θερμότητας όσο διεισδύει εντός της δοκού. Αυτό ισχύει είτε έχουμε περιστροφή είτε όχι. Η περιστρεφόμενη δοκός έχει περισσότερη συνολική κινητική ενέργεια από εκείνη που δεν περιστρέφεται. Ωστόσο, και στις δύο περιπτώσεις έχουμε την ίδια ποσότητα μεταφορικής κινητικής ενέργειας. Αυτό συμφωνεί με το γεγονός ότι οι δύο δοκοί ανεβαίνουν στο ίδιο ύψος.

Γιάννης Γαϊσίδης

gaisidis@viewonphysics.gr

Visited 392 times, 1 visit(s) today

4 Comments

Add a Comment

Γιάννης Γαϊσίδης

31 Μαΐου 2015 at 20:08
Με βάση το άρθρο, για τους μαθητές της Γ΄ Λυκείου προτείνω το παρακάτω πρόβλημα:

Μία σφαίρα όπλου εκτοξεύεται με ταχύτητα 400m/s κατακόρυφα προς τα πάνω εναντίον ακίνητης ομογενούς ξύλινης δοκού σχήματος παραλληλεπιπέδου και σφηνώνεται εντός αυτής.

Δίνονται: Η μάζα της σφαίρας και της δοκού m=20gr και M=1,4Kg αντίστοιχα. Η ροπή αδράνειας του συσσωματώματος δοκός-σφαίρα ως προς άξονα που διέρχεται απο το κέντρο μάζας Ι=5,8×10^-3 Kgxm². g=10m/s²

Για τις δύο περιπτώσεις:

A. Η κατεύθυνση της σφαίρας να περνάει από το κέντρο μάζας της δοκού και

B. Η κατεύθυνση της σφαίρας να περνάει από σημείο που απέχει από το κέντρο μάζας της δοκού απόσταση d=0,1m

υπολογίστε:
1. Την ταχύτητα του συσσωματώματος μετά την κρούση.
2. Το κλάσμα της κινητικής ενέργειας της σφαίρας που μεταφέρεται στο συσσωμάτωμα.
3. Σε ποιο ύψος από την αρχική θέση της δοκού ανεβαίνει το συσσωμάτωμα μετά το κτύπημα από τη σφαίρα.
4. Σε ποια από τις δύο περιπτωσεις που εξετάζουμε η σφαίρα θα διεισδύσει πιο βαθιά στη δοκό και γιατί;
Απάντηση
1. Βιδάλης Δημήτριος
  
  13 Ιουνίου 2015 at 12:54
  
  Εξαιρετική ανάλυση! Συγχαρητήρια!
  
  Απάντηση
  1. Γιάννης Γαϊσίδης
    
    13 Ιουνίου 2015 at 13:28
    
    Δημήτρη ευχαριστώ για τα καλά σου λόγια. Η άποψή σου πάντα με ενδιαφέρει.
    
    Απάντηση
2. Γεώργιος
  
  18 Αυγούστου 2015 at 16:27
  
  Υπεροχο σάιτ πολυ ενδιαφέρων
  
  Απάντηση