- Του Lewis Epstein
- Απο το βιβλίο “Εικόνες της Σχετικότητας” εκδόσεις Κάτοπτρο.
Μια μικρή και εκλαϊκευμένη εισαγωγή στον κόσμο της Ειδικής Θεωρίας της Σχετικότητας και στην έννοια του χωρόχρονου.
Ερώτηση:Γιατί δεν μπορούμε να ταξιδέψουμε ταχύτερα από το φως;
Απάντηση::Επειδή δεν μπορούμε να ταξιδέψουμε με μικρότερη ταχύτητα από αυτό.
Υπάρχει για όλα τα πράγματα μία μόνο ταχύτητα. Οτιδήποτε υπάρχει γύρω μας, κινείται πάντοτε με την ταχύτητα του φωτός. Θα αναριωτιέστε. Πώς γίνεται να κινείστε αφού κάθεστε αναπαυτικά στην πολυθρόνα σας; Η απάντηση είναι ότι κινείστε μέσα στο χρόνο.
Γι αυτό αντιλαμβανόμαστε τα χρονόμετρα που ταξιδεύουν μέσα στο χώρο να “δουλεύουν” πιο αργά. Επειδή κανονικά τα χρονόμετρα “τρέχουν” μέσα στο χρόνο και όχι μέσα στο χώρο. Αν τα αναγκάσουμε να κινηθούν μέσα στο χώρο, θα το κάνουν δαπανώντας ένα μέρος της ταχύτητας που χρησιμοποιούν να ταξιδέουν μέσα στο χρόνο. Όσο μάλιστα ταχύτερα ταξιδεύουν μέσα στο χώρο τόσο πιο αργά ταξιδεύουν μέσα στο χρόνο. Είναι επίσης δυνατόν να τα αναγκάσουμε να δαπανήσουν ολόκληρη την ταχύτητα που χρησιμοποιούν, για να ταξιδεύουν μόνο μέσα στο χώρο. Τότε όμως θα ταξιδεύουν μόνο μέσα στο χώρο και καθόλου μέσα στο χρόνο (αφού δε θα τους έχει απομείνει άλλη ταχύτητα).Θα ‘χουν σταματήσει να χρονομετρούν, επομένως θα ‘χουν σταματήσει να “γερνούν”.
Όλα αυτά μπορεί να παρασταθούν με ένα διάγραμμα, το οποίο στην ουσία είναι το “κοσμικό ταχύμετρο”. Τίποτα δεν μπορεί να μεταβάλλει την “ολική” ταχύτητα ενός σώματος. Μόνο η διεύθυνση της κίνησής του, μέσα στο χωρόχρονο, μπορεί να μεταβληθεί.
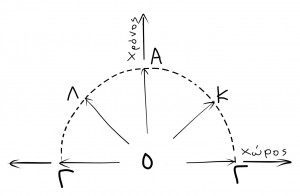
Εικ. 1. Το θέμα είναι ένα: ότι πάντα κινείστε, και μάλιστα με σταθερή ταχύτητα. Ακόμη κι όταν μένετε ακίνητοι.Σ’ αυτή την περίπτωση ταξιδεύετε μέσα στο χρόνο, από το Ο στο Α. Όταν η ταχύτητά σας έχει τέτοια κατεύθυνση που σας μεταφέρει μέσα στο χώρο, π.χ. από το Ο στο Κ ή στο Λ, τότε μειώνεται η συνιστώσα που απομένει για να σας μεταφέρει μέσα στο χρόνο. Στην περίπτωση που η ταχύτητα δαπανιέται εξ ολοκλήρου για να σας μεταφέρει μέσα στο χώρο (με την ταχύτητα του φωτός), δεν απομένει καθόλου ταχύτητα για να σας μεταφέρει μέσα στο χρόνο, και κινείστε από το Ο στο Γ. Επειδή η ταχύτητά σας μέσα στο χωρόχρονο είναι σταθερή, τα τμήματα ΟΑ, ΟΚ, ΟΛ και ΟΓ έχουν ίσα μήκη και τα σημεία Α,Κ,Λ και Γ βρίσκονται πάνω σε ένα ημικύκλιο γύρω από το Ο. Αν μπορούσατε να ταξιδέψετε πίσω στο χρόνο, το ημικύκλιο θα γινόταν πλήρης κύκλος.
Σε κατάσταση ηρεμίας το σώμα θεωρείται ότι ταξιδεύει μέσα στο χρόνο και το διάνυσμα της ταχύτητάς του βρίσκεται πάνω στον άξονα του χρόνου και κατευθύνεται από το Ο προς το Α. Όταν όμως κινείται προς τα δεξιά ή προς τα αριστερά, το διάνυσμα της ταχύτητάς του κλίνει προς τα δεξιά, π.χ. προς το Κ ή προς τα αριστερά, προς το Λ αντίστοιχα. Στην ακραία περίπτωση, όταν η κίνηση γίνεται εξ ολόκληρου στο χώρο και καθόλου στο χρόνο, τότε το διάνυσμα κατευθύνεται από το Ο προς το Γ.
(περισσότερα…)
Μου αρέσει αυτό:
Like Φόρτωση...